改进共轭梯度法求解无约束二次凸规划问题
乔熔岩, 赵新国
(1.中国人民解放军装备学院 研究生二队,北京 101416; 2.中国人民解放军装备学院 航天指挥系,北京 101416)
1 引 言
共轭梯度法在构造共轭方向时,初始方向选定为已知点的负梯度方向,有一定的局限性,而且采取边搜索边构造的方式,构造过程比较复杂.本文将对经典共轭梯度法进行改进,即先利用n的任一组正交基,直接构造出一组共轭方向,然后让初始点沿这组方向进行一维最优搜索,求出极小值点.
2 改进共轭梯度法的基础理论
2.1 共轭方向的构造通式
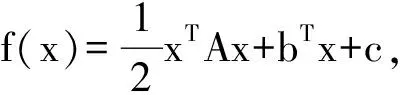
取d1=α1. 因为
(1)
所以取d2=A-1α2. 构造d3=α3+k1d1,令
(2)
(3)
这说明上述构成的d3与d1,d2关于A共轭. 再构造d4=A-1α4+p1d2,令
(4)
(5)
(6)
这说明所构成的d4也与d1,d2,d3关于A共轭.
现将此构造方法进行推广,给出d2m-1和d2m(其中m=1,2,3,…)的构造通式
d2m-1=α2m-1+k1d1+k2d3+…+km-1d2m-3,
(7)
d2m=A-1α2m+p1d2+p2d4+…+pm-1d2m-2.
(8)
令
(9)
由式(9)得
再令
(10)
由式(10)得
由此可根据通式(7),(8),构造出一组方向d1,d2,…,dn.
2.2 构造方法的理论证明
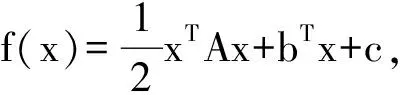
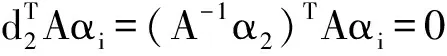
(11)
即αi与d2m关于A共轭,根据数学归纳法可知定理1成立.
定理2已知
其中x∈n,A为n阶正定矩阵,b为n维列向量,c为常数,方向d1,d2,…,dn是由一组正交基α1,α2,…,αn,根据通式(7),(8)构造的,现任取向量αj(其中j为偶数),则有A-1αj与d1,d3,…,d2m-1关于A共轭,其中2m-1≤n,m=1,2,3,….
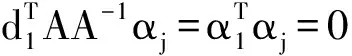
(12)
即A-1αj与d2m-1关于A共轭,根据数学归纳法可知定理2成立.
现利用定理1和定理2,来证明由通式(7)和(8)所构造的d1,d2,…,dn是关于A共轭的.
由式(1)~(6)可知,d1,d2,d3和d4是关于A共轭的. 现假设已构造的d1,d2,…,d2m-3,d2m-2关于A共轭,其中2m-2 (13) (14) 第一:确定初始点x0、精度ε和一组正交基α1,α2,…,αn(可取单位坐标基); 第二:利用式(7),(8)直接构造出一组方向d1,d2,…,dn关于A共轭; 第三:以x0为起点,首先沿方向d1进行一维最优步长搜索,求出步长λ1和x1=x0+λ1d1.如果‖f(x1)‖≤ε,则停止搜索,求出f(x1);否则再以x1为起点,沿方向d2进行一维最优步长搜索,以此类推,直到找到满足精度要求的点为止. 已知 其中x∈n,A为n阶正定对称矩阵,b为n维列向量,c为常数,d1,d2,…,dn是由一组正交基α1,α2,…,αn,根据通式(7),(8)构造的关于A共轭的方向,以任意点x0为起点,依次沿d1,d2,…,dn进行一维最优步长搜索,得到点x1,x2,…,xn,其中λ1,λ2,…,λn为相应的最优步长,则xn是f(x)的唯一极小点. 证由3.1中的方法可知 则有 (15) 任取方向dj(其中j=1,2,…,n),则有 (16) (17) 根据最优步长λj的求解过程可知,λj是式(18)的解 (18) (19) 其中j=1,2,…,n. 又设存在一组数β1,β2,…,βn,使得 (20) (21) 分别用共轭梯度法和改进共轭梯度法求解如下问题: 初始点x0=(5,5)T,求解过程如表1所示. 表1 两种方法的计算步骤 由表1所示,改进共轭梯度法比共轭梯度法在求解例题时,计算步骤要减少一步,其主要原因是,共轭梯度法在构造d2之前,要多计算一步求去解f(x1),而改进共轭梯度法则不用. 现将3.3中f(x)推广为n元函数,则利用共轭梯度法求解时,每构造新的搜素方向之前,都要多计算一步去求解上一点的梯度,这就在整体计算步骤上,比改进共轭梯度法多出n-1步. 从构造搜索方向的方法来看,共轭梯度法的初始方向选定为初始点的负梯度方向,且新方向的构造也必须借助于上一点的梯度. 而改进共轭梯度法则不同,它在构造搜素方向时,不用依赖于负梯度方向,只要任意给出一组正交基,就可以直接构造出所有的搜素方向. 而在选取正交基时,一般取单位坐标基即可,这样非常简单方便. 本文首先对经典的共轭梯度法进行了分析,指出了其在构造共轭方向上的局限性和复杂性. 然后根据二次正定函数的特性,对经典方法进行了改进,并利用数学归纳法对其进行了证明,同时给出了方法应用时的具体计算步骤,并对方法的收敛性进行了证明.从实例求解的结果看,该方法的计算步骤要比共轭梯度法少,在求解搜素方向时,也具有一定的灵活性和应用价值. [参 考 文 献] [1] 陈宝林.最优化理论与算法[M]. 2版. 北京:清华大学出版社,2005:120-360. [2] 陈庆华,郭全魁,宋华文.装备运筹学教程[M].北京:国防工业出版社,2007:1-50. [3] 《运筹学》教材编写组.运筹学[M].北京:清华大学出版社,1994:1-120. [4] 张俊学.作战运筹学[M].北京:解放军出版社,2000:1-200. [5] 邓乃扬.无约束最优化方法[M].北京:科学出版社,1982:20-50. [6] Powell M J D.Nonlinear optimizatiion[M]. London:Academic Press,1982:1-10. [7] Luenberger D G..Introduction to linear and nonlinear programming[M]. Addison-wesley,1984:1-50. [8] Avril M..Nonlinear programming: analysis and methods[M].Prentice-Hall, Inc.,1976:20-30. [9] 席少霖,赵凤治.最优化计算方法[M].上海:上海科学技术出版社,1983:25-120.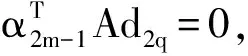
3 改进共轭梯度法的应用
3.1 方法的基本计算过程
3.2 方法收敛性的证明




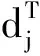
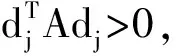
3.3 实例求解与比较

4 总 结

