线性弹性问题的异质多尺度—间断有限元方法

余 涛

线性弹性问题的异质多尺度—间断有限元方法

余 涛

（井冈山大学数理学院，江西，吉安 343009）

在异质多尺度方法的框架下，使用内部惩罚间断有限元方法作为宏观求解器，构造了多尺度线性弹性问题的异质多尺度—间断有限元方法，并且给出了介质是周期情况下的最佳误差估计。

多尺度线性弹性问题；异质多尺度方法；间断有限元方法

1 引言

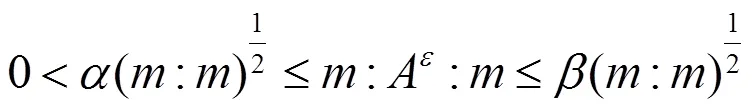
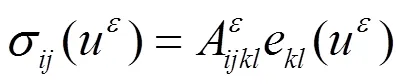
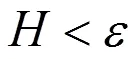
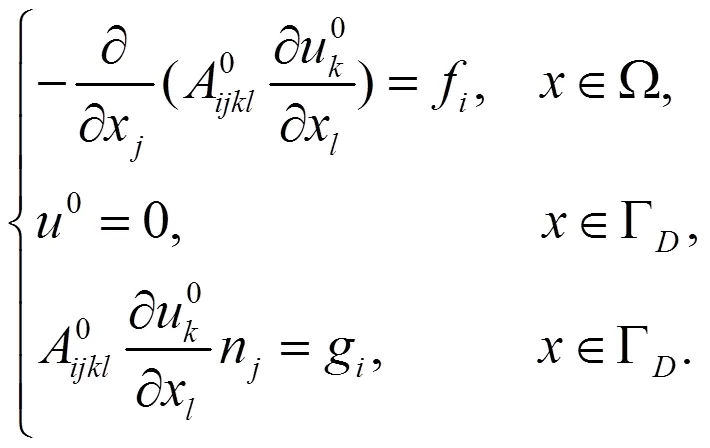
显然，上述均匀化方程(1.5)可以在粗网格上用传统的方法求解，这样也就得到了问题(1.1)的宏观解。但是，只有对介质有严格的假设条件的基础上[1]，才可以得到此方程均匀化系数0的具体表达式。

为了在不知道均匀化系数0的具体表达式的情况下去求解上面的均匀化问题(1.5)，就需要构造多尺度算法。现有的多尺度算法包括：广义有限元方法[3]、多尺度有限元方法[4]、变分多尺度方法[5]、无残差Bubble方法[6]以及异质多尺度方法[7]等等。

本文将采用异质多尺度方法去求解方程（1.5）。它由两部分组成：粗网格上选取一个宏观求解器和估计宏观求解器中的未知宏观数据。在异质多尺度方法的框架下，选取不同的宏观求解器就可以得到不同的算法。针对线性弹性问题，文献[8]中采用有限元方法作为宏观求解器，得到了相应的算法和误差估计。最近，Abdulle将异质多尺度方法和间断有限元方法相结合提出了求解纯扩散问题的算法[9]，并且给出了详细的误差分析[10]。本文将这种方法应用到线性弹性问题上得到相应的结果。

2 多尺度线性弹性问题的异质多尺度—间断有限元方法

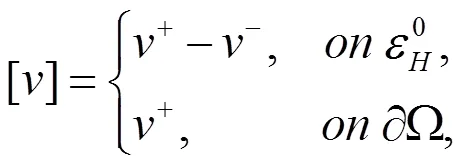
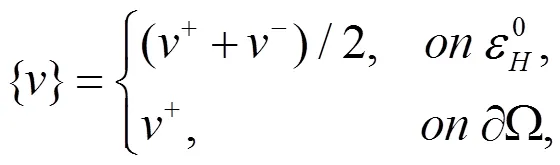
考虑分片多项式间断有限元空间

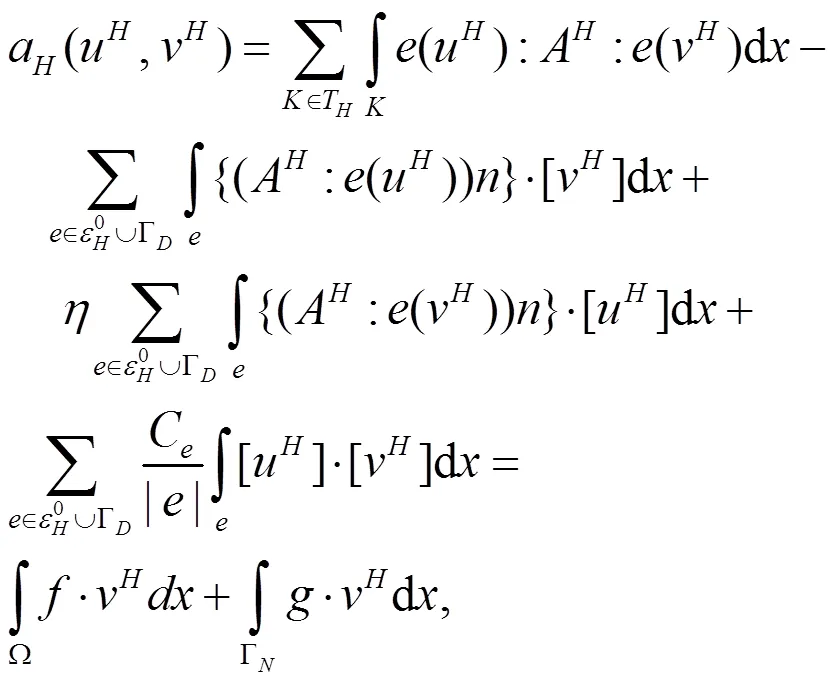
考虑数值积分格式

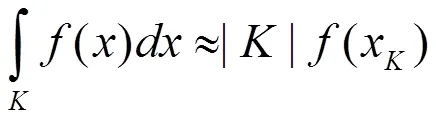
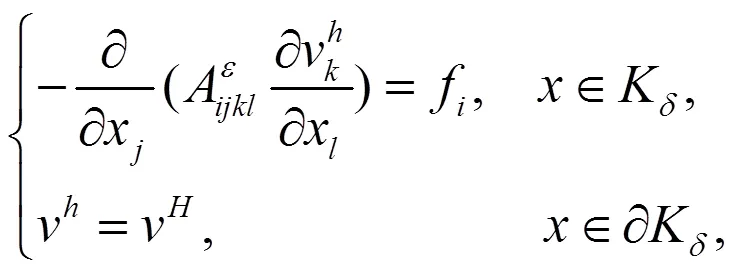
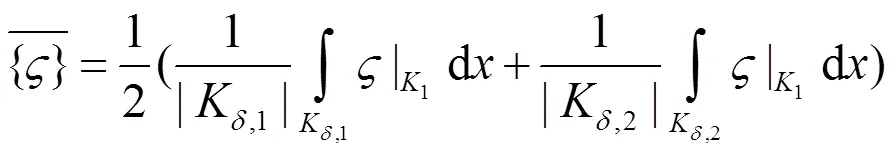
进而，可以得到如下改进的双线性形式

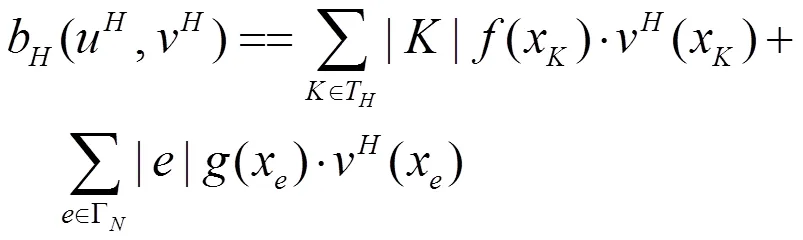
3 误差估计

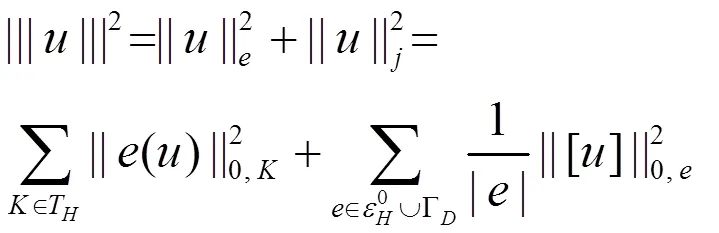
根据内部惩罚间断有限元方法的误差估计[5]，可知宏观误差

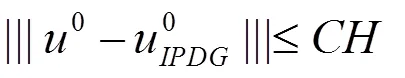
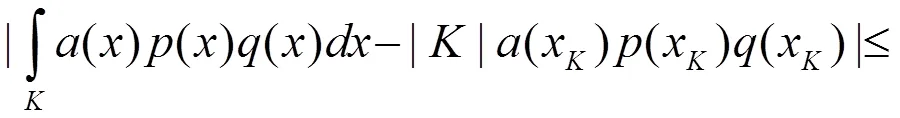
和

易得

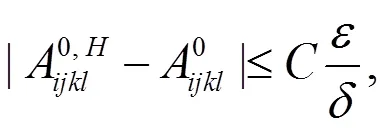
从而，模型误差

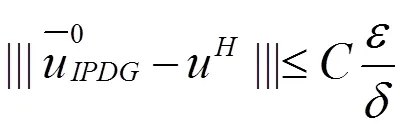
结合（3.2）~（3.5）式，有

[1] Ciarlet P G. The finite element method for elliptic problems[M]. Elsevier, 1978.

[2] Bensoussan A,Lions J L,Papanicolaou G. Asymptotic Analysis for Periodic Structures, Studies in Mathematics and its Applications[M].New York: North-Holland Publication, 1978.

[3] Babuška I, Osborn J E. Generalized finite element methods: their performance and their relation to mixed methods[J]. SIAM Journal on Numerical Analysis, 1983, 20(3): 510-536.

[4] Hou T Y, Wu X H. A multiscale finite element method for elliptic problems in composite materials and porous media[J]. Journal of computational physics, 1997, 134(1): 169-189.

[5] Franca L P, Russo A. Deriving upwinding, mass lumping and selective reduced integration by residual-free bubbles[J]. Applied mathematics letters, 1996, 9(5): 83-88.

[6] Hughes T J R. Multiscale phenomena: Green's functions, the Dirichlet-to-Neumann formulation, subgrid scale models, bubbles and the origins of stabilized methods[J]. Computer methods in applied mechanics and engineering, 1995, 127(1): 387-401.

[7] Weinan E,Engquist B. The heterogeneous multi-scale methods[J]. Commun. Math. Sci., 2003, 1:87-132.

[8] Abdulle A. Analysis of a heterogeneous multiscale FEM for problems in elasticity[J]. Mathematical Models and Methods in Applied Sciences, 2006, 16(04): 615-635.

[9] Abdulle A. Multiscale method based on discontinuous Galerkin methods for homogenization problems[J]. Comptes Rendus Mathematique, 2008, 346(1): 97-102.

[10] Abdulle A. Discontinuous Galerkin finite element heterogeneous multiscale method for elliptic problems with multiple scales[J]. Mathematics of Computation, 2012, 81(278): 687-713.

[11] Arnold D N. An interior penalty finite element method with discontinuous elements[J]. SIAM journal on numerical analysis, 1982, 19(4): 742-760.

HETEROGENEOUS MULTISCALE-DISCONTINUOUS GALERKIN METHOD FOR PROBLEMS IN LINEAR ELASTICITY

YU Tao

(School of Mathematics and Physics, Jinggangshan University,Ji’an, Jiangxi 343009, China)

We develop an interior penalty discontinuous Galerkin finite element method (IPDG-FEM) based on the heterogenous multiscale method (HMM), for the multiscale linear elasticity problems. The optimal error estimate is given for periodic media.

multiscale linear elasticity problems; heterogeneous multiscale method; discontinuous Galerkin method

O242.1

A

10.3969/j.issn.1674-8085.2014.04.006

1674-8085(2014)04-0027-04

2014-02-09；

2014-03-11

江西省自然科学基金项目(20132BAB211018)；吉安市软科学计划项目(吉市科计字[2012]32-7)；井冈山大学博士科研启动基金项目(JZB11002).

余 涛(1983-)，男，江西万安人，讲师，博士，主要从事多尺度建模研究(E-mail: yutao@jgsu.edu.cn).