几类微分方程零解的不稳定性*

郭怡萍，冯滨鲁

(1．山东科技大学数学与系统科学学院，山东 青岛266590;2．潍坊学院，山东 潍坊261061)

引言

由于低阶微分方程的稳定性与不稳定性与实际生活有着密切的关联，而且研究低阶系统所得到的结果与方法，往往为研究高阶系统提供依据．因此，对于低阶微分方程的稳定性与不稳定性研究变得十分重要．目前，对于低阶微分方程稳定性的研究成果已经有很多，关于不稳定性的研究成果却较少［1～4］．本文通过构造适当的Liapunov函数，研究自治微分方程和非自治微分方程零解不稳定的充分条件．

1 关于自治微分方程解的不稳定性

1．1 基本理论

对于自治系统

这里xi=col(x1，x2，···，xn)，fi(x)连续可微，fi(0)≡0．

引理1［1］(Krasovskii)若存在可微函数V(x)，V(0)=0在原点任意邻域内，存在x0，使V(x0)＞0;又且不含式(1)的非平凡的整条正半轨线，则式(1)的平凡解不稳定．

1．2 主要结果

研究方程:

其中a是常数，f(0，0，0，0)=0，f、g、φ是所依赖变量的连续函数．得到如下结果，即定理1．

定理1 若不等式

对任意y，z，u均成立，则对任意常数a和函数g，方程的零解是不稳定的．

证明 构造V函数［5］如下:

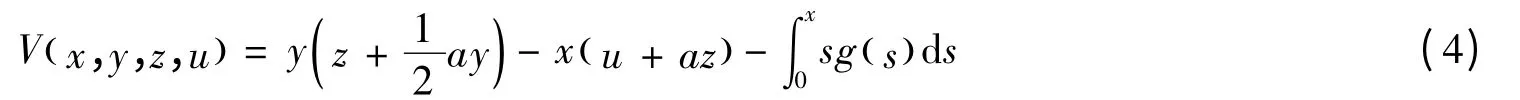
因此，在(x，y，z，u)空间原点的任意领域内，存在一点使得

方程(2)的等价系统为:

设(x，y，z，u)= (x(t)，y(t)，z(t)，u(t))是系统(5)的一个解，则沿这一解对式(4)关于时间t求导得:

所以，根据Krasovskii定理知方程(2)的零解是不稳定的．

研究方程:

其中a、b是常数，a≠0，f(0，0，0，0，0)=0，f、g和ψ是所依赖变量的连续函数．得到如下结果，即定理2．

定理2 若不等式:

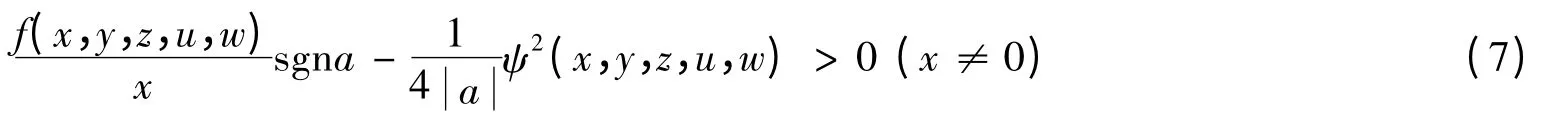
对任意y，z，u和w成立，则对任意常数b和函数g，方程(6)的零解是不稳定的．

证明 定义函数W=W(x，y，z，u，w)如下:

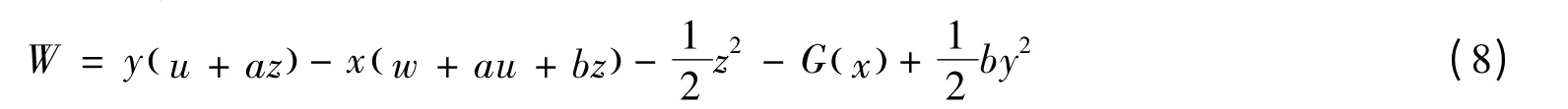
因此在(x，y，z，u，w)空间原点的任意邻域内，存在一点使得

方程(6)的等价系统为:

令(x，y，z，u，w)= (x(t)，y(t)，z(t)，u(t)，w(t))是系统(10)的任一解，则函数V沿系统(10)的任一解关于时间t的导数为:

即:

因此，由Krasovskii定理知，方程(6)的零解是不稳定的．

1．3 应用举例

例1 应用定理1判断下面变系数四阶微分方程的零解是否稳定．

其中g( )x是关于x的连续函数．

求解如下．

将式(12)化为等价的方程组:

式中:

显见有:

由于(1+y2)2＞1，故从而满足了定理1的全部条件，故知微分方程(6)的零解是不稳定的．

易见此例运用以往的判定准则是无法判定的．

例2 应用定理2判断下面变系数五阶微分方程的零解是否稳定．

其中g( )x是关于x的连续函数．

求解如下．

将式(14)化为等价的方程组:

式中:

显见有:

从而满足了定理2的全部条件，故知微分方程(14)的零解是不稳定的．

易见此例运用以往的判定准则是无法判定的．

2 关于非自治微分方程解的不稳定性

2．1 基本理论

对于非自治系统

这里xi= (x1，x2，···，xn)，fi(t，x)连续可微，fi(t，0)≡0，下面的引理对此部分定理的证明是需要的．

引理2［1］若存在定义在t≥t0，‖x‖＜H上的可微函数V t，( )x，V t，( )0 =0，满足以下条件:

1)在原点的任何领域内有V t，( )x＞0的区域;

2)V t，( )x具有无穷小上界;

则系统(16)的零解是不稳定的．

2．2 主要结果

研究下列一类三阶非线性非自治微分方程:

这里g(0)=h(t，0)≡0，e(t，0，0，0)≡0，且满足解的存在唯一性要求．得到定理3．

定理3 对于方程(17)，若存在常数α＞0，L＞0，0＜δ＜1，满足条件:

2)h(t，x)≤j(x)，xh(t，x)≥0，yg(y)≥0;

3)ze(t，x，y，z)≥0，r˙(t)＜0．

则方程(17)的零解是不稳定的．

证明 将微分方程(17)化为等价的方程组［6］:

取Liapunov函数:

由条件1)、2)得:

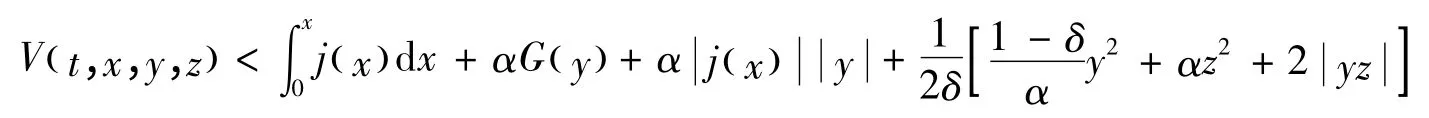
从而V(t，x，y，z)具有无穷小上界．又:

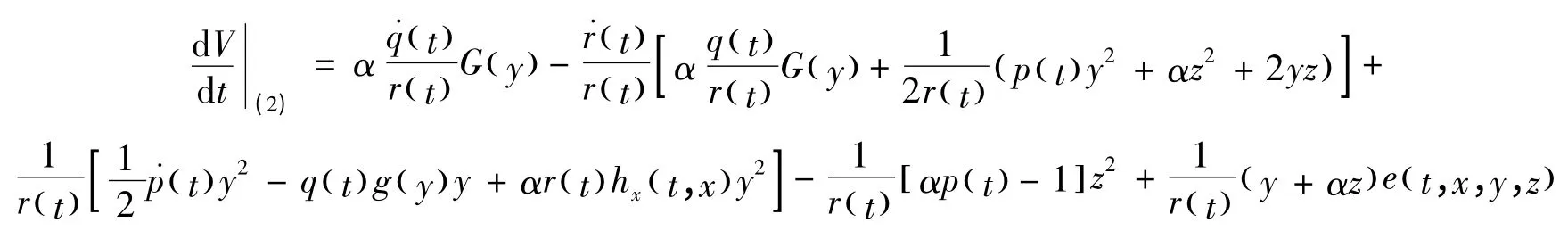
据条件1)、3)，在区域Ω中有:

这样就满足了引理的全部条件，从而判知方程(17)的零解是不稳定的．

2．3 应用举例

应用定理3判断下面变系数五阶微分方程的零解是否稳定．

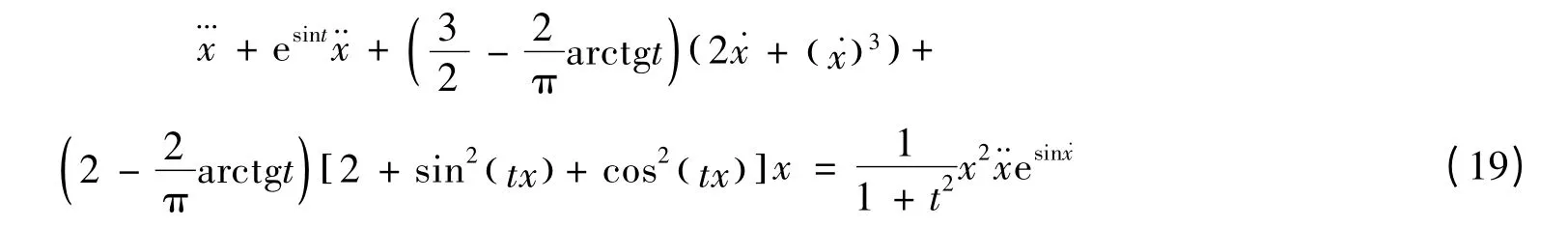
求解如下．

将式(19)化为等价的方程组:

式中:

且:

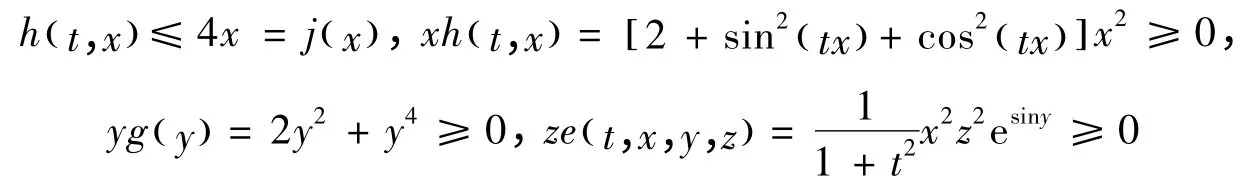
从而满足了定理的全部条件，故知微分方程(19)的零解是不稳定的．

易见此例运用以往的判定准则是无法判定的．

［1］廖晓昕．稳定性的数学理论及应用［M］．武昌:华中师范大学出版社，1988．

［2］韩振来，冯滨鲁，张玉峰．一类三阶非自治微分方程的不稳定性［J］．济南大学学报，1996，3(6):48－50．

［3］Ezcilo J O C．Instability Theorems for Certain Fifth－order Differential Equation［J］．Math Proc Camb Phil Soc，1978，5(16):110－113．

［4］Ezcilo J O C．An Instability Theorem for a Certain Sixth－order Differential Equation［J］．Austral Math Soc(Series A)，1982，6(32):129－133．

［5］卢德渊．一类三阶非线性微分方程解的不稳定性［J］．应用数学和力学，1995，9(12):17－23．

［6］冯滨鲁．两类非线性系统的不稳定性［J］．山东矿业学院学报，1992，11(2):200－203．