数学分析与复变函数课程教学内容的类比分析

张节松

(淮北师范大学数学科学学院，安徽淮北235000)

数学分析和复变函数是数学专业的两门重要基础课，前者建立在实数域上，后者以复数为自变量讨论问题。由于实数为复数的特殊子集，这两门课程在教学内容上存在诸多类似之处。鉴于复变函数为数学分析的后续课程，恰当地将二者进行类比不仅能帮助学生理解，还可以激发他们的学习热情，启发他们的科研意识。例如，在教学实践中曾有学生问道:在数学分析中，讲完单变量微积分，还讲授了多变量微积分，为什么在复变函数课程中没有多变量函数的理论呢?这是根据两课程联系而提出的一个自然问题，然而回答起来却并不容易。实际上，多复变分析已成为当代数学研究的一个主流方向[1]。恰当地应用数学分析知识帮助解决一些复分析问题，也可以使学生温故知新，培养他们运用已学知识解析问题的能力。

需要说明的是，只有部分数学分析的结论在复变函数中得以保持，有些却有所差异，甚至截然不同。因此，在复变函数的课程教学中探究哪些可以保持、哪些不再成立、有什么内在的本质原因等问题，显得尤为重要，也是学生学习和运用复变函数知识时需要特别注意的。另外，对于那些不再成立的结论，是否存在复数域内的相应形式，如果存在又是什么?这些问题同样值得探讨。

出于上述考虑，本文首先将数学分析与复变函数这两门课程的相关教学内容进行类比，分别指出在复变函数中得以保持和不能照搬的结论并给予讨论，对部分在复数域内不再成立的结论指出了相应研究成果。并结合数学分析知识证明复变函数的一些结论，进一步明晰这两门课程的联系。

1 教学内容的类比

1.1 数与函数

与实数域的情形相同，复数满足运算的一般定律，加法遵守交换律与结合律，乘法遵守交换律与结合律且遵守乘法对加法的分配律。根据解析函数的惟一性定理这一内在原因，一切代数恒等式在复数域内仍然成立，如a2－b2=(a+b)(a－b)。对数函数的基本性质也是成立的，如ln(z1z2)=lnz1+lnz2，ln(z1/z2)=lnz1－lnz2等。关于复指数函数ez，就实数z=x来说，复指数函数ez的定义与实指数一致，ez在复平面上也是可微且满足加法定理的，即(ez)'=ez，ez1+z2=ez1ez2。类似地，正弦函数sinz和余弦函数cosz对于z为实数来说，一致于数学分析情形，在z平面上可微且(sinz)'=cosz，(cosz)'=－sinz。同样，sinz是奇函数，cosz是偶函数，并遵从通常的三角恒等式，如sin2z+cos2z=1，sin(z1+z1)=sinz1cosz2+cosz1sinz2;它们都是以2π为周期的周期函数;sinz的零点还是z=nπ，cosz的零点还为z=(n+1/2)π。此外，完备性定理(如波尔查诺(Bolzano)－魏尔斯特拉斯定理、闭集套定理、海涅－波莱尔(Heine－Borel)覆盖定理也依然保持。

但是，与实数域内|sinx|≤1的情形不同，正余弦函数ez在复数域内均不再有界;复指数函数ez变成了以2πi为周期的周期函数;在数学分析中，指数函数ex与三角函数sinx、cosx没有直接关联，而在复变函数中，它们通过尤拉公式eiz=cosz+i sinz进行沟通;在实对数函数中，负数是没有对数的，而复对数函数可以对任何一个非零复数定义，并且正实数的复对数是无穷多值的;复变函数的极限的定义与单变元实变函数的极限概念尽管形式上一样，但极限要求z要沿着任意方向趋向z0时的极限均相同。对比数学分析中一元实变函数f(x)的极限，指在实轴上x只沿x0左右两个方向，复变函数极限存在的要求显然苛刻得多，这也是复变函数与数学分析的根本性区别。可微且不恒为零的实变函数，其零点不一定孤立，可微且不恒为零的解析函数，其零点则必然孤立;有界闭区域上的实连续函数，其最大值不一定在边界上取得，而复变函数中存在最大模定理，有界闭区域上非常数的解析函数一定在边界上达到最大值。

1.2 函数的导数与中值定理

数学分析中函数求导包括复合函数求导的法则在复变函数中仍然保持，洛必达(L’Hospital)法则也是成立的。关于复变函数中洛必达法则的详细讨论可参见文献[2－3]。不过，数学分析的主要研究对象为连续函数，复变函数则主要研究解析函数。解析是较连续强得多的条件，也具有更多的良好性质，如无穷可微性、幂级数展开等。这些对于连续函数而言是绝不可能的，因为其导函数不一定存在;在数学分析中，处处连续而处处不可微的函数很难得到，需要复杂的构造，而在复函数中几乎随手可得。

由文献[4]可知，数学分析的微分中值定理不能直接推广到复平面，关于其内在原因的探讨可参见文献[5]。那么在复数域内，是否存在相应形式的中值定理?文献[6]研究了这一问题，遗憾的是其立论基础(定理1)并不成立[7]。文献[8]进一步讨论了该问题，得到了复函数的一个一般性微分中值公式。

1.3 积分

从定义上看，实、复积分都是分割、取近似值、求和取极限的思路，复变函数积分保持着黎曼积分的大部分基本性质，如线性性、分段积分不变性、积分与路径的无关性、绝对值不等式、连续必可积，可积必有界等。重要的牛顿－莱布尼茨公式也相应成立(需在单连通区域内且解析)。复积分建立在复平面上，实为沿曲线积分，相当于两个二元实函数的线积分，格林公式搭建了沿闭曲线积分与二重积分的联系。

在计算方法上，解析函数积分的计算更加灵活多样，数学分析中的积分中值定理不能直接推广到复积分上来，如

关于复变函数和数学分析主要内容的类比以及类比教学法在复变函数教学中应用的讨论还可参见文献[5，9 －10]。

2 数学分析在复变函数课程教学中的应用

2.1 一个注记的证明

在复变函数的经典教材[4](第111页)有一个注记但未予证明，即“设E、F是平面上两个点集，ρ(E，F)=是点集E与F的距离。若E，F是两不相交的闭集，且E有界，则有ρ(E，F)＞0”。下面应用数学分析的知识给予证明。

根据下确界的定义，存在点列{ξn}⊂E与{ηn}⊂F，使

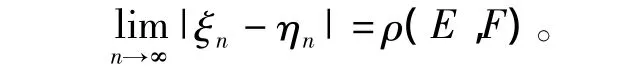
由于E有界，所以{ξn}有界。由波尔查诺(Bolzano)－魏尔斯特拉斯定理，存在子列{ξnk}收敛于z1，且因E为闭集，z1∈E。此时易见{ηnk}也有界，因而它有子列{ηnkj}收敛于一点z2∈F，对应的子列{ξnkj}仍是收敛于 z1的。于是

因 E∩F=∅，故 z1≠z2，所以 ρ(E，F)＞0。

2.2 柯西积分定理的证明

柯西积分定理被认为是研究复变函数的一把钥匙，此定理由柯西于1825年提出，黎曼首先在添加条件“f'(z)在D内连续”的前提下给予了证明，古尔萨(Goursat)不添加任何条件给出了定理的完全证明。文献[4]采用了古尔萨证明，但其过程较为繁琐，不便于在教学实践中讲授。文献[11]利用调和分析的方法给出了一个新的证明，其中还用到了控制收敛定理等实分析的高级工具。若采用该证法，则知识点可能超纲。为此，文献[12]利用数学分析的知识构造了一个简单的恒同逼近函数。由此应用逼近思想，成功地用满足柯西－黎曼条件的连续可微的函数逼近一般的可微函数，给出了柯西积分定理的一个初等证明，方便了复变函数论中这一关键性定理证明的教学。

2.3 亚纯函数在周线C内至多只有有限个内部零点和极点的证明

设(1)C是一条周线，f(z)在C的内部是亚纯的，且连续到C;(2)f(z)沿C不为零，则(试证)函数f(z)在C的内部至多只有有限个零点和极点。

对于该问题，文献[13]给出了分析。从严格意义上还需证明D1为区域。为避免这一问题，下面结合数学分析知识，给出新证法。

(反证)假设f(z)在C内有无限多个极点，根据聚点定理知，存在极点列{zn，n≥1}使zn→z∈C0+C，下证a也是f(z)的极点。若不然，由题设条件知f(z)在a点连续，因此ε=1对，必存在σ1＞0，使得只要|z－a|＜σ1，就有|f(z)－f(a)|＜1。

根据zn→a知，对σ1＞0，存在N使得当n＞N 时，有|zn－a|＜σ1，特别地，|zN+1－a|＜σ1。由于 zN+1∈⊙(a，σ1)，所以存在 σ2＞0，使得圆⊙(zn+1，σ2)⊂⊙(a，σ1)。又由 zN+1为极点，所以对 M=|f(a)|+2，存在σ3＞0，使得只要0＜ |z－zN+1|＜σ3，就有|f(z)|＞M=|f(a)|+2。

于是，当0＜ |z－zN+1|＜min(σ2，σ3)时，有|z－a|＜σ1，|f(z)|＞ |f(a)|+2且|f(z)－f(a)|＜1。由此推出|f(a)|=|f(a)－f(z)+f(z)|≥|f(z)|－|f(z)－f(a)|＞|f(a)|+2－1=|f(a)|+1。

则产生矛盾。可见，当极点无限多时，所求得的极限点a亦为极点，鉴于zn→a，显然不可能为孤立奇点，即极点a非孤立。

因为f(z)连续到C，所以a必然属于C的内部C0，注意到a为函数1/f(z)的零点，而a非孤立，其任意邻域内还存在函数1/f(z)的其它零点，这与解析函数零点的孤立性矛盾。可见函数f(z)的极点不可能无限多，于是结论得证。

实际上，利用数学分析证明复分析结论的例子还很多，如函数解析的充要条件[12]等。另外，利用复分析知识同样可解决数学分析的相关问题，如幂级数理论的本质描述、利用留数定理计算实积分等。这很好地诠释了数学的奥秘在于它们相通而不是孤立的存在。

3 结语

在复变函数的课程教学中，常常能感受到其与数学分析课程有着诸多近似，但差异之处同样不时出现，因此需要谨慎对待。本文类比了这两门课程主要教学内容的内在联系与区别，为复变函数课程的教学提供参考，有利于学生增强联想、猜想以及探索的意识。同时，这也启示我们在复变函数的教学实践中对可移植的内容适当复习并说明一致性即可;对差异之处要特别强调，以避免学生想当然地照搬数学分析的知识点，出现理解错误、应用不当的情况。另外，还应将数学分析的相关知识点引入复分析若干结论的证明中，以促进新旧知识衔接，帮助学生融会贯通不同学科的知识，培养自如运用所学知识创新的意识和能力。

[1]史济怀，刘太顺.复变函数[M].合肥:中国科学技术大学出版社，1998.

[2]张庆.复变函数论与数学分析中一些问题的比较[J].唐山师范学院学报，1998(5):10.

[3]吴琼，宋儒瑛.复变函数中的罗必达法则[J].太原师范学院学报:自然科学版，2006，5(2):14－16.

[4]钟玉泉.复变函数论[M].3版，北京:高等教育出版社，2004.

[5]杨吉英.关于复变函数和数学分析主要内容的类比[J].赤峰学院学报:自然科学版，2013(17):12－13.

[6]石平绥.复分析的中值理论[J].曲阜师范大学学报:自然科学版，1993(1):101－104.

[7]李兴民，叶平柱.关于“复分析的中值理论”一文的评注[J].曲阜师范大学学报:自然科学版，1993(4):16.

[8]周永正.复函数微分中值公式的注记[J].数学的实践与认识，1998(4):340－344.

[9]姜淑珍.关于复变函数论教学方法的思考[J].长春师范学院学报:自然科学版，2005，23(2):122－124.

[10]胡燧林.努力沟通数学分析课及其后继课程之间的横向联系——复变函数论教学的点滴体会[J].韶关师专学报，1987(2):16－31.

[11]王信松，陆斌.柯西积分定理的一个新证明[J].数学的实践与认识，2006，35(9):195－197.

[12]王信松，张节松.复变函数[M].合肥:中国科学技术大学出版社，2011.

[13]钟玉泉.复变函数学习指导书[M].北京:高等教育出版社，1995.