二维3 态Potts 量子系统的保真度与序参量

李生好，伍小兵，黄崇富，范奇恒

(重庆工程职业技术学院，重庆400037)

1 引 言

近年来，保真度作为来自于量子信息与量子计算领域的基本概念，不但可以来刻画量子系统的量子相变，而且还可以来描述量子系统的任何内部序引起的任何类型的相变，这说明保真度开创了凝聚态物理学、量子信息与量子计算理论之间的一个重要的视角［1］. 量子相变包含着丰富的物理信息，怎样抓住量子相变中最关键的物理信息是凝聚态物理研究领域的重点和难点，而保真度与序参量恰恰则提供了一个非常简洁的度量手段，来解决这个问题.

在数值模拟领域，近年来张量网络算法取得了巨大的进展. 所谓张量网络算法，是指一系列张量乘积态表示的算法的统称，包括一维的矩阵乘积态(iMPS)算法［2］，二维的纠缠投影对态(iPEPS)算法［3，4］，任意维的多尺度纠缠重整化(MERA)算 法［5，6］，Graded PEPS (gPEPS)算法［7，8］，以及准一维——自旋梯子量子系统的算法［9］等. 通过将张量网络算法与保真度相结合，能够研究量子多体系统的量子相变和量子临界现象.

最近，人们对于量子q 态Potts 模型比较感兴趣［10，11］，其中q =2 时，即为著名的Ising 模型.对于一维量子q 态Potts 模型来说，当q =2 与3时，该模型系统发生二级相变［12］;当q ＞3 时发生一级相变. 而对于二维量子q 态Potts 模型来说，当q=2 时，毫无疑问，此时即为Ising 模型，系统发生二级相变;那么当q=3 时，即3 态Potts模型会发生一级相变或二级相变?下面，基于iPEPS 张量网络算法，从基态保真度、约化保真度、普适序参量和局域序参量的角度，对二维量子3 态Potts 模型展开研究，该模型在对称破缺相中存在三个简并的基态.

2 理论模型和数值算法

现在考虑无限外加磁场二维正方格子量子3态Potts 模型的哈密顿量:

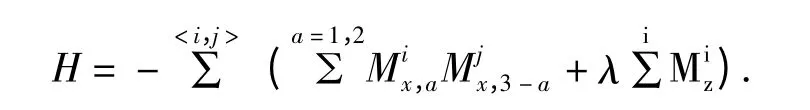
在无限大的二维正方格子平面上， ＜i，j ＞表示所有的最近邻对;i (j)是表示第i (j)个格点;Mi

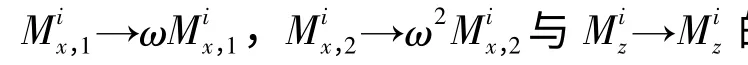
3 数值模拟结果

3.1 基态保真度

基态保真度是来自于量子信息与量子计算领域的一个基本概念，它能够很好地描述任何一个量子多体关联系统的量子相变，而与这个系统的内部序是传统的对称破缺序还是新颖的拓扑序［13］无关. 在量子信息与量子计算理论中，任何两种态的重叠表示一种态向另一种态的变化［14，15］，可以用保真度描述这两种态的相似程度［16，17］.

对于以外加磁场为控制参量的二维正方格子量子3 态Potts 模型，运用iPEPS 算法来进行数值模拟，能够得到量子系统的基态波函数. 对于系统的两个不同的控制参量λ1 和λ2，分别对应的基态波函数为| Ψ(λ1)＞和| Ψ(λ2)＞，定义这两个基态波函数的系统基态保真度为F(λ1，λ2)= | ＜Ψ(λ2)| | Ψ(λ1)＞| . 当二维量子系统为有限的N 个格点时，那么平均单点基态保真度d(λ1，λ2)与系统基态保真度F(λ1，λ2)的关系为d(λ1，λ2)= F(λ1，λ2)1/N，也就可以得到Ind(λ1，λ2)=InF(λ1，λ2)/N.

运用iPEPS 算法，数值模拟无限二维量子3态Potts 模型时，只需每次任意选取初态就能得到三种不同对称性的基态波函数，就能有效地计算基态保真度，也由此可以得到基态保真度在二维平面上的分叉. 如果选择在Z3群对称区的外加磁场λ2 的波函数| Ψ(λ2)＞作为参考态，此时单点基态保真度d(λ1，λ2)是不能区分在Z3对称性破缺区的外加磁场λ1 的三个简并基态的. 如果选择在Z3群对称破缺区的外加磁场λ2 的波函数| Ψ(λ2)＞作为参考态，此时单点基态保真度d(λ1，λ2)就能区分在Z3对称性破缺区的外加磁场λ1 的三个简并基态的，其中分叉的上支是一个简并基态，分叉的下支是两个简并基态的重合.图1 画出外加磁场的二维量子3 态Potts 模型的单点基态保真度d(λ1，λ2)的分叉. 这里选择在Z3群对称破缺区的外加磁场λ2 =2.1 时的基态波函数| Ψ(λ2)＞作为参考态，单点基态保真度d(λ1，λ2)通过分叉，是可以区分三个简并基态的，分叉点就是相变点［18］λc≈2.61，在分叉点处基态保真度不连续，因而这是一个一级相变点.

这里，系统相变点λc以分叉点［19］的形式表现出来的. 单点基态保真度分叉使人们探测系统的相变点时，不需要对系统的控制参量进行求微分那样复杂，其优势在于是普适的，是与模型无关的，因而更具有实际意义.

图1 二维量子3 态Potts 模型单点基态保真度Fig.1 The ground -state fidelity per lattice site for quantum 3 - state Potts model in two spatial dimensions

3.2 约化保真度

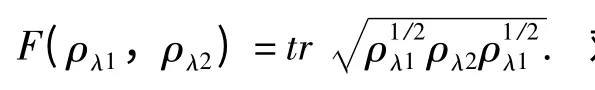
这里分别计算了无限外加磁场二维正方格子3 态Potts 模型的单点和两点约化保真度. 图2 中选取了破缺Z3群对称的λ2=2.1 处的ρλ2作为参考态，画出了无限外加磁场二维正方格子3 态Potts 模型的单点(红色三角形表示)与两点(蓝色空心圆表示)约化保真度F(ρλ1，ρλ2). 很容易看出，单点与两点约化保真度能够从三个简并基态波函数中，区分任意两个约化密度矩阵所描述的混合态，其中分叉的上支是一个简并基态，分叉的下支是两个简并基态的重合. 单点与两点约化保真度中的分叉点是一致的，而分叉点就是相变点λc≈2.61. 当控制参量外加磁场λ1逐渐增大越过相变点λc时，基态简并情况会突然变化，从而表现出系统正经历着一个量子相变. 也很容易得到，分叉点就是相变点，并且在分叉点处约化保真度不连续，说明这是一个一级相变点.

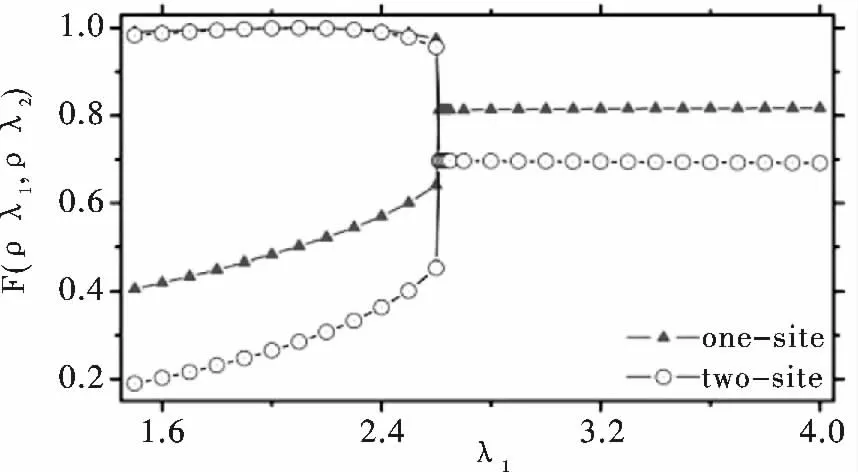
图2 二维量子3 态Potts 模型的单点和两点约化保真度的分叉Fig.2 The ground - state one - and two - site reduced fidelity for quantum 3 -state Potts model in two spatial dimensions

3.3 普适序参量

对于一个有着对称群Z3的外加磁场的二维正方格子量子3 态Potts 系统，在经历一个一级量子相变点中有一个普适序参量［21］. 所谓普适序参量，是一个基态波函数| Ψ ＞与这个基态波函数的对称变换g | Ψ ＞之间的距离的某种单点保真度. 普适序参量对于二级相变是连续的，而对于一级相变是不连续的和跳跃的. 考虑在二维正方格子量子3 态Potts 模型系统的任何一个基态波函数| Ψ ＞，对于对称算符z3群中的非零对称算符g∈{I，ω，ω2}，其中w = exp (i2π/3)，对于这个基态波函数| Ψ ＞的对称变换g | Ψ ＞，有单点保真度fg(λ) | 〈Ψ| g| Ψ〉.

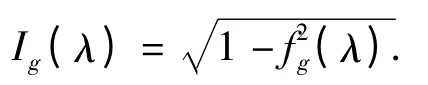
图3 画出的是外加磁场λ 为控制参量的无限二维正方格子量子3 态Potts 模型的的普适序参量Ig(λ). 随着外加磁场λ 的增大，在λc处，普适序参量Ig(λ)从非零的变为零，特别是外加磁场λ 变化跨过相变点λc≈2.61 时，普适序参量Ig(λ)是不连续的，显示出系统在相变点处经历了一个一级量子相变.

图3 二维量子3 态Potts 模型的普适序参量Fig.3 The universal order parameter for quantum 3 -state Potts model in two spatial dimensions

3.4 局域序参量

局域序参量可以用来区分系统的两个基态波函数的状态. 一般来说，当系统经历量子相变时，其没有发生对称性自发破缺的这一相的局域序参量一般为零;而发生了对称性自发破缺的这一相的局域序参量一般不为零. 对于不同的系统，局域序参量的结构和含义会有所不同，局域序参量既可以是标量或矢量，也可以是实数或复数，局域序参量还可能是多分量的. 这里，对于二维Potts 模型就具有多分量的复数局域序参量.

系统基态波函数的PEPS 张量网络表示可以有效提取某一个局域序参量. 一旦确定了系统的相变点λc，根据不同区域的λ ＞λc与λ ＜λc的两个基态波函数，就可以分别得到两个不同的单点约化密度矩阵ρ. 可以看到，3 态Potts 模型在λ＞λc与λ ＜λc的这两个区域中的单点约化密度矩阵ρ 展现出不同的非零项的结构. 在外加磁场λ＞λc的区域，自发磁化强度＜＞或＜＞为零;而在外加磁场λ ＜λc的区域，自发磁化强度＜＞或＜＞不为零，此时， ＜＞ =＜＞，但＜＞或＜＞可能为复数. 这意味着外加磁场二维量子3 态Potts 模型存在着一个局域序参量Sx= ＜＞或Sx= ＜＞，来刻画在外加磁场变化下量子3 态Potts 模型有着一级相变. 对于二维量子3 态Potts 模型，在运用iPEPS 算法进行数值模拟时，只需选取任意初态就很容易得到三个简并的基态，从而可以得到自发磁化强度 (局域序参量)Sx有 | Sx| ，ω| Sx| 与| Sx| 的三个取值，其中ω = exp(i2π/3)，即系统局域序参量有3 个，其中2 个为复数. 对于外加磁场λ 小于相变点，自发磁化是一个非零值，一旦外加磁场λ 大于相变点λc，自发磁化将跳跃为零. 在图4 中，画出了不同外加磁场λ 下三个简并基态的自发磁化强度(局域序参量)的实部Re (Sx)与虚部Im (Sx)的三维图，都说明了在相变点λc≈2.61 处均会发生一个不连续的跳跃，这里是一个一级相变点.

图4 二维量子3 态Potts 模型的自发磁化强度(局域序参量)的实部与虚部Fig.4 The real and imaginary part of the magnetization for quantum 3 -state Potts model in two spatial dimensions

4 结 论

本文主要基于二维量子系统的iPEPS［3，4］算法，从单点基态保真度、约化保真度、普适序参量和局域序参量的角度，来研究二维正方格子量子3 态Potts 模型的量子相变和量子临界现象，均得出系统发生一级相变，而对于二维量子2 态Potts 模型，也就是Ising 模型来说，系统发生二级相变. 也提供了一个思路，基于包含iPEPS 算法在内的张量网络算法，从单点基态保真度、约化保真度、普适序参量和局域序参量方面，可能运用在不同维数的量子多体系统，来探测系统任何类型的量子相变.在研究过程中，发现算法的精度和效率还有待继续提高，例如使用二维量子系统的iPEPS 算法对二维量子q 态Potts 模型进行数值模拟，当q＞3 时，普通台式计算机将无法进行计算模拟或模拟速度非常缓慢. 还有算法模拟的有限截断维数也受限于目前计算机的能力. 下一步从系统的量子相变和量子临界现象的理解入手，需要进一步优化和发展包括iPEPS 在内的张量网络算法，来提高计算机模拟的精度和效率.

［1］ Tommaso R，Paola V，Andrea F，et al. Studying quantum spin systems through entanglement estimators ［J］.Phys. Rev. Lett.，2004，93:167203.

［2］ Vidal G. Classical simulation of infinite-size quantum lattice systems in one spatial dimension ［J］. Phys. Rev.Lett.，2007，98:070201.

［3］ Jordan J，Orus R，Vidal G，et al.Classical simulation of infinite-size quantum lattice systems in two spatial dimensions ［J］. Phys. Rev. Lett.，2008，101:250602.

［4］ Li B，Li S H，Zhou H Q.Quantum phase transitions in a two - dimensional quantum XYX model:Ground -state fidelity and entanglement ［J］. Phys. Rev. E，2009，79:060101(R).

［5］ Vidal G. Entanglement renormalization［J］. Phys.Rev.Lett.，2007，99:220405.

［6］ Evenbly G，Vidal G. Algorithms for entanglement renormalization［J］. Phys. Rev. B，2009，79:144108.

［7］ Shi Q Q，Li S H，Zhao J H，et al. Graded projected entangled-pair state representations and an algorithm for translationally invariant strongly correlated electronic systems on infinite - size lattices in two spatial dimensions［J］. arXiv:0907.5520.

［8］ Li S H，Shi Q Q，Zhou H Q. Ground-state phase diagram of the two-dimensional t-J model［J］. arXiv:1001.3343.

［9］ Li S H，Shi Q Q，Su Y H，et al. Tensor network states and ground - state fidelity for quantum spin ladders［J］.Phys.Rev.B，2012，86:064401.

［10］ Potts R B. Some generalized order -disorder transformations［J］. Proc. Cambridge Philos. Soc.，1952.48:106.

［11］ Wu F Y. The Potts model［J］. Rev. Mod. Phys.，1982，54:235.

［12］ Dai Y W，Hu B Q，Zhao J H，et al. Ground-state fidelity and entanglement entropy for the quantum threestate Potts model in one spatial dimension ［J］. J.Phys. A:Math. Theor.，2010，43:372001.

［13］ Zhou H Q，Barjaktarevic J P. Fidelity and quantum phase transitions ［J］. J. Phys. A:Math. Theor.，2008，41:412001.

［14］ Alberti P M. Stochastic linear maps and transition probability［J］. Lett. Math. Phys.，1983，7:25.

［15］ Wootters W K. Statistical distance and Hilbert space［J］. Phys. Rev.D，1981，23:357.

［16］ Jozsa R. A new proof of the quantum noiseless coding theorem［J］. J. Mod. Opt.，1994，4l:2315.

［17］ Schumacher B. Quantum coding［J］. Phys. Rev. A，1995，51:2738.

［18］ Zhao J H，Wang H L，Li B，et al. Spontaneous symmetry breaking and bifurcations in ground-state fidelity for quantum lattice systems ［J］. Phys. Rev. E，2010，82:061127.

［19］ Crawford J D. Introduction to bifurcation theory［J］.

Rev. Mod. Phys.，1991，63:991.

［20］ Liu J H，Shi Q Q，Zhao J H，et al. Quantum phase transitions and bifurcations:reduced fidelity as a phase transition indicator for quantum lattice many - body systems［J］. J. Phys. A:Math. Theor.，2011，44:495302.

［21］ Liu J H，Shi Q Q，Wang H L，et al. Universal construction of order parameters for translation -invariant quantum lattice systems with symmetry-breaking order［J］. Phys. Rev. E，2012，86:020102.