计算树的[1,2]-数的算法研究

张 超,赵承业

(中国计量学院 理学院,浙江 杭州 310018)

计算树的[1,2]-数的算法研究

张 超,赵承业

(中国计量学院 理学院,浙江 杭州 310018)

图G的一个点集S是[1,2]-集,若每个不在S中的点至少与S中的1个点相邻且至多与S中的2个点相邻.一个图的所有[1,2]-集中元素个数最小的集合,其元素个数称为图的[1,2]-数.针对树的[1,2]-数的计算问题进行研究.首先,根据[1,2]-数的定义给出了一个0-1规划模型,求解这个0-1规划可以得到图的[1,2]-数的精确值.然后,基于贪婪策略将树进行星分解,给出计算[1,2]-数的两个近似算法.最后,分析了两个近似算法的计算复杂度和性能.

[1,2]-数;0-1规划;贪婪策略;近似算法

一个集合S⊆V(G)被称为图G的支配集(Dominating Set)[1],如果其满足下面的条件:对图G的任意的顶点v,或者属于S或者与S中的顶点相邻接.我们把顶点数目最少的支配集称为图的最小支配集(Minimum Dominating Set),它的顶点数目称为图的支配数(Dominating Number),记作γ(G).对于支配集S,若有任意的点v∈V(G)S满足1≤|N(v)∩S|≤2,则此支配集S为图G的[1,2]-集[2],其最小阶数即为图的[1,2]-数([1,2]-number),记作γ[1,2](G).

支配集在许多计算机领域有广泛的应用,例如连通支配集在无线网络的虚拟骨干构造中具有很重要的应用价值.[1,2]-集的概念是CHELLALI[2]等人2013年提出的一类受限的支配集的概念.他们给出了一般的[j,k]-集的概念,即满足j≤|N(v)∩S|≤k的集合,并重点讨论了j=1,k=2,3情形下的一些问题.他们证明了一般二分图的[1,2]-集问题是一个NPC问题,因此计算图的[1,2]-数问题是一个比较复杂的问题.

本文针对最简单的连通图——树,考虑树的的[1,2]-数的计算问题.我们首先考虑计算树的[1,2]-数精确算法,由[1,2]-数定义我们建立0-1规划模型,通过求解0-1规划模型得到树的[1,2]-数的精确值.考虑到0-1规划的局限性(能计算的顶点数有限),我们基于贪婪策略给出了两个近似算法,分析了其计算复杂性并通过实验分析了这两个算法的性能.

1 计算[1,2]-数的0-1规划模型

对任意一个图G有邻接矩阵A,I为单位矩阵,令向量X=(x1,x2,…,xn),其中xj表示图G中的顶点,若在[1,2]-集中则赋值为1;反之,不在[1,2]-集中赋值为0,则图G的[1,2]-数即为式(1)0-1规划模型的解.

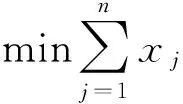
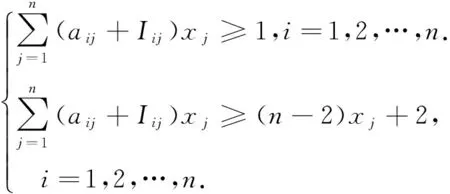
(1)

式(1)中：xj=0,1,i=1,2,…,n.

图1是一棵20个顶点的树,利用上面的0-1规划模型求解此树的[1,2]-数,如图所示,其中黑色的节点构成了这个图的[1,2]-集,其精确值为7.

因为一般0-1规划的求解,其复杂性是指数阶的,因此利用上面的0-1规划模型求解树的[1,2]-数有很大的局限性.我们使用处理器为ADM Athlon(tm)Ⅱ X3 425@2.7 GHz的计算机,利用Matlab R2009a中的优化工具箱中相关函数编写了求解上面0-1规划模型的程序.通过大量的数据实验表明,此模型适用范围在400个顶点以下.

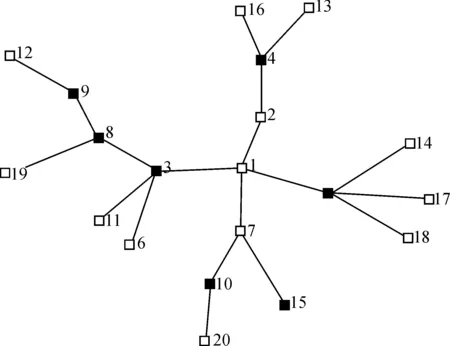
图1 0-1规划模型计算20个顶点的树的[1,2]-数Figure 1 0-1 programming model calculating [1,2]-number of tree with 20 vertices

2 基于贪婪策略的计算树的[1,2]-数的近似算法

借鉴文献[3]中构造连通支配集的近似算法的思想,先利用贪婪策略构造一个图的支配集,然后再添加一些点到这个支配集中直到满足[1,2]-集的条件.基于不同贪婪策略,得到的近似算法也不同.我们下面给出两个近似算法:基于顶点的最大度对树进行星分解;基于具有最多叶子的节点对树进行星分解.

2.1 基于顶点的最大度MD(Maximum Degree)

对任意一棵树以当前最大度顶点为中心进行星分解.首先,删除选择的最大度点及其相邻点和边,树的余下部分依次循环此操作直至剩下的点为孤立点或孤立点集,那么每次找到的最大度点和最后剩下的孤立点就构成一个集合C,并且C之外的点若与C内的点相邻个数超过2时要把该点加入集合C,从而最终得到的集合C就是这个树的[1,2]-集,其中集合C的节点元素个数即为该算法计算得到的树的[1,2]-数.

算法2.1 基于最大度点的近似算法(MD Algorithm)

输入:任意一棵树T.

输出:T的[1,2]-集C的阶数.

算法描述:

C=φ,W=V;

选取树T最大度节点c,C=C∪{c},W=W-N[c];

WhileW不是孤立点集

do 选取T[W]的最大度节点c,C=C∪{c},W=W-N[c];

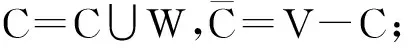
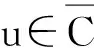
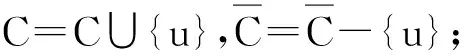
计算集合C的节点个数.

定理2.1 算法2.1的时间复杂度是O(n2)的,其中n是树的顶点数.

证明:算法2.1的时间复杂度主要依赖两个while循环的时间复杂度.

第一个while循环,判断W是否为孤立点集的时间复杂度是O(n)的;寻找T[W]的最大度节点的复杂度也是O(n)的;因此第一个while循环的复杂度是O(n2)的.

第二个while循环,判断是否存在满足要求的u的时间复杂度是O(n)的;C和它的补集的增减操作的时间复杂度都是O(n)的;因此第二个while循环的复杂度是O(n2)的.

其他操作的时间复杂度不超过O(n)的,因此算法2.1的时间复杂度是O(n2)的.

图2给出对图1中的同一棵树,MD算法的计算结果.MD算法计算速度比0-1规划模型有显著地提高,但相应地计算精度下降了.根据树结构的特点,我们进行了改进,给出了基于最多叶子节点的近似算法.

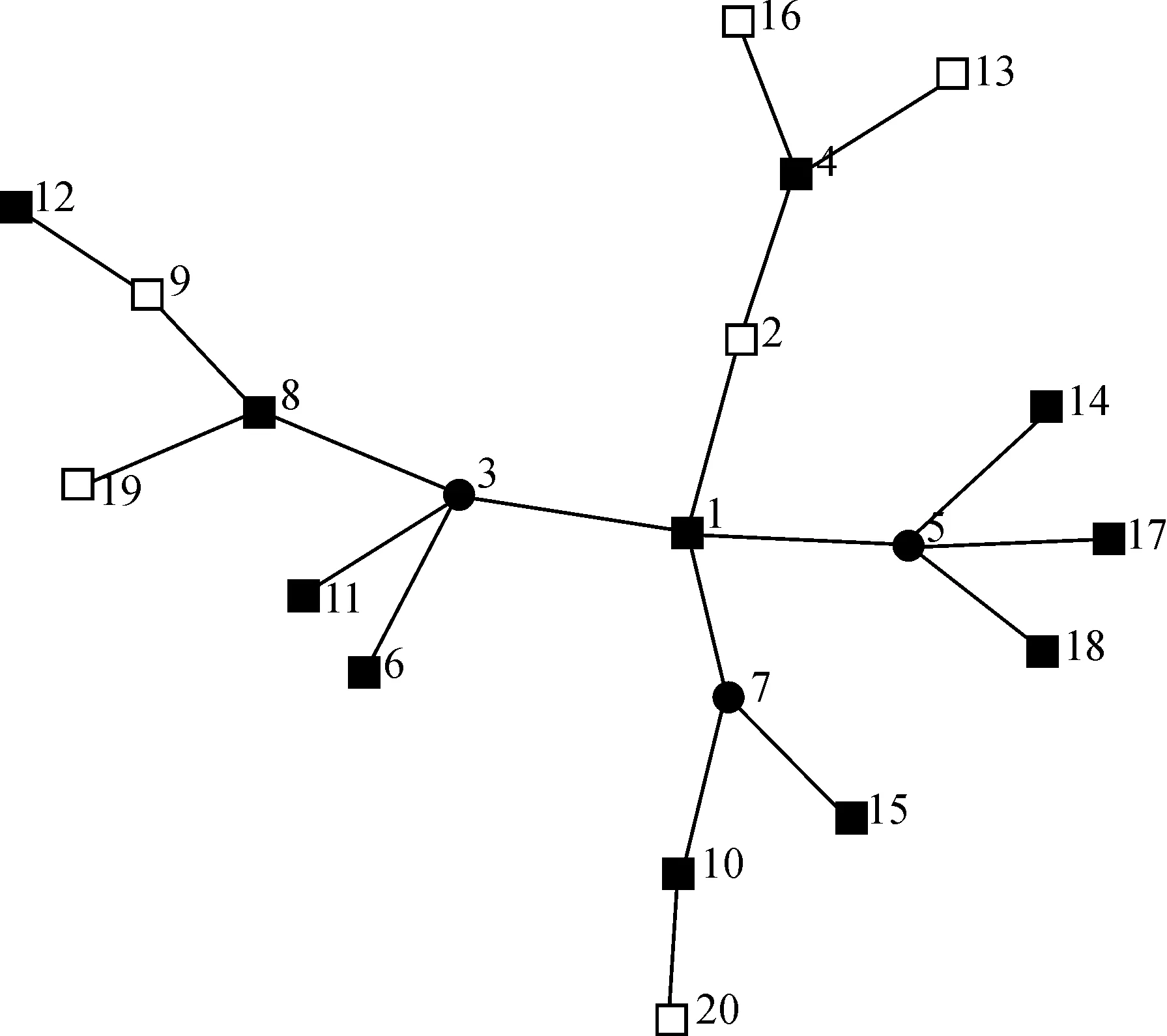
图2 基于最大度点的近似算法计算20个顶点的树的[1,2]-数Figure 2 Calculating [1, 2]-number of tree with 20 vertices by MD Algorithm

2.2 基于最多叶子的节点ML(Maximum Leaves)

考虑到MD算法可以在删除节点时,令许多叶子节点变成孤立点,造成许多不必要的顶点也进入到集合C中,我们在选择星结构的中心点时,把最大度改成有最多叶子的节点,就可以避免这种情况,基于这个思想,我们给出下面的算法:

算法2.2 基于最多叶子节点的近似算法(ML Algorithm)

输入:任意一棵树T.

输出:T的[1,2]-集C的阶数.

算法描述:

C=φ,W=V;

选取树T中叶子最多的节点c,C=C∪{c},W=W-N[c];

WhileW不是孤立点集

do 选取T[W]中叶子最多的节点c,C=C∪{c},W=W-N[c];

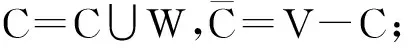
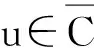
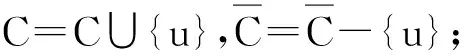
计算集合C的节点个数.

定理2.2 算法2.2的时间复杂度是O(n3)的,其中n是树的顶点数.

证明:算法2.2的时间复杂度主要依赖两个while循环的时间复杂度.

第一个while循环,判断W是否为孤立点集的时间复杂度是O(n)的;寻找T[W]的有最多叶子的节点复杂度是O(n2)的;因此第一个while循环的复杂度是O(n3)的.

第二个while循环,判断是否存在满足要求的u的时间复杂度是O(n)的;C和它的补集的增减操作的时间复杂度都是O(n)的;因此第二个while循环的复杂度是O(n2)的.

其他操作的时间复杂度不超过O(n2)的,因此算法2.2的时间复杂度是O(n3)的.

图3给出对图1中的同一棵树ML算法的计算结果.

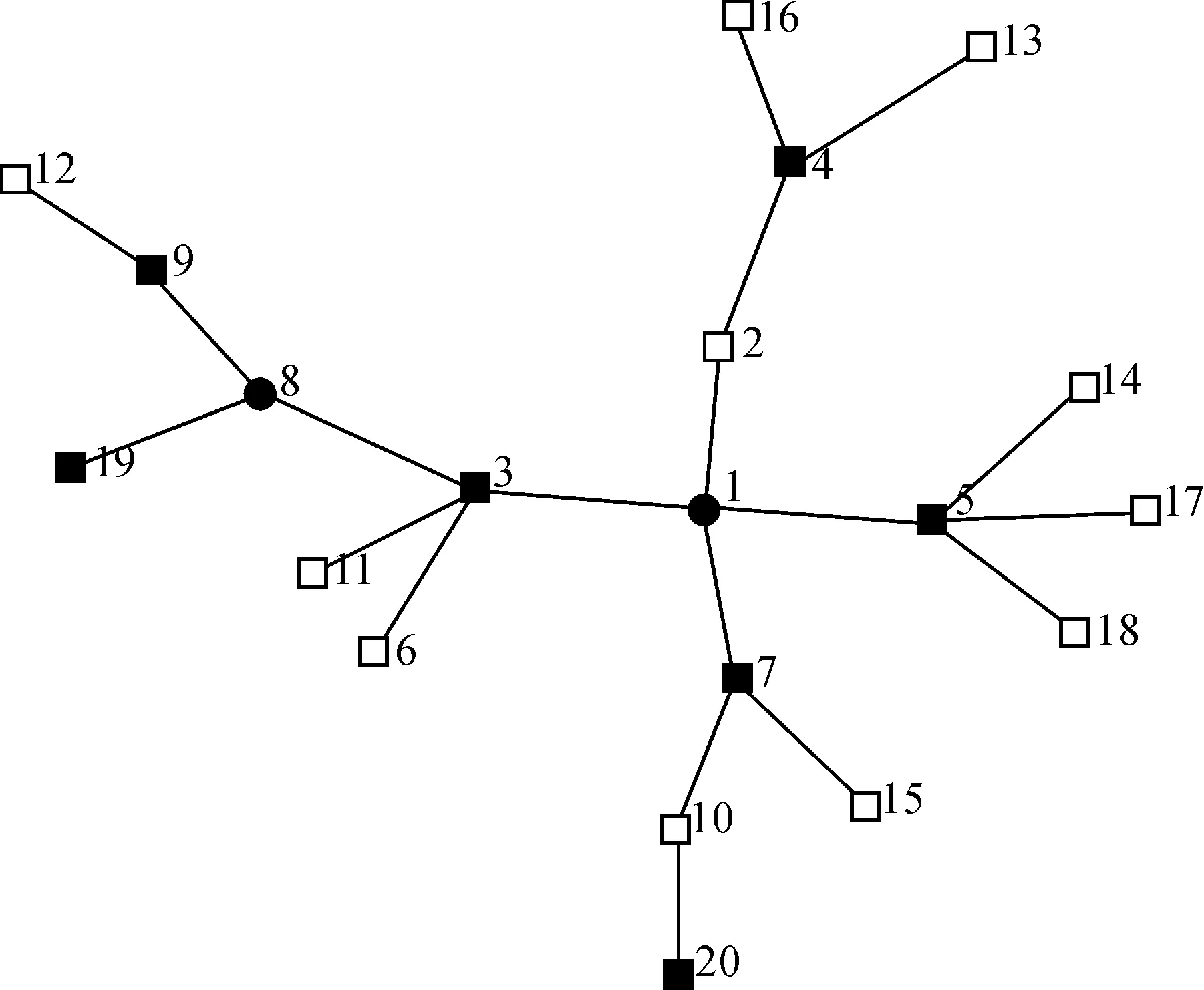
图3 基于最多叶子的近似算法计算20个顶点的树的[1,2]-数Figure 3 Calculating [1, 2]-number of tree with 20 vertices by ML Algorithm

3 实验结果与对比分析

综合上述的两类算法,分别为0-1规划模型(IP)的精确算法和两种基于贪婪策略的近似算法,其中近似算法包括基于寻找最大度点图分解的算法(MD)和基于寻找最多叶子节点图分解的算法(ML).本文中所有的实验均是使用ADM Athlon(tm)Ⅱ X3 425@2.7 GHz处理器在Matlab R2009a环境下运行.下面针对这三种算法,在算法的时间复杂度和结果的精确性两方面上进行对比分析.

3.1 时间复杂度对比分析

表1 计算不同节点个数的树的[1,2]-数的平均运行时间(s)

Table 1 Average running time calculating [1,2]-number of trees with different vertices (s)

顶点个数基于最大度基于最多叶子0-1规划500.0052450.0166110.1097531000.0163320.0715651.8410172000.0540450.46417114.4288793000.1377521.61154966.0506374000.2490353.229548209.5409734500.4108245.219620—

3.2 精确性对比分析

表2 不同节点个数的平均计算结果

Table 2 Average calculation results with different vertices

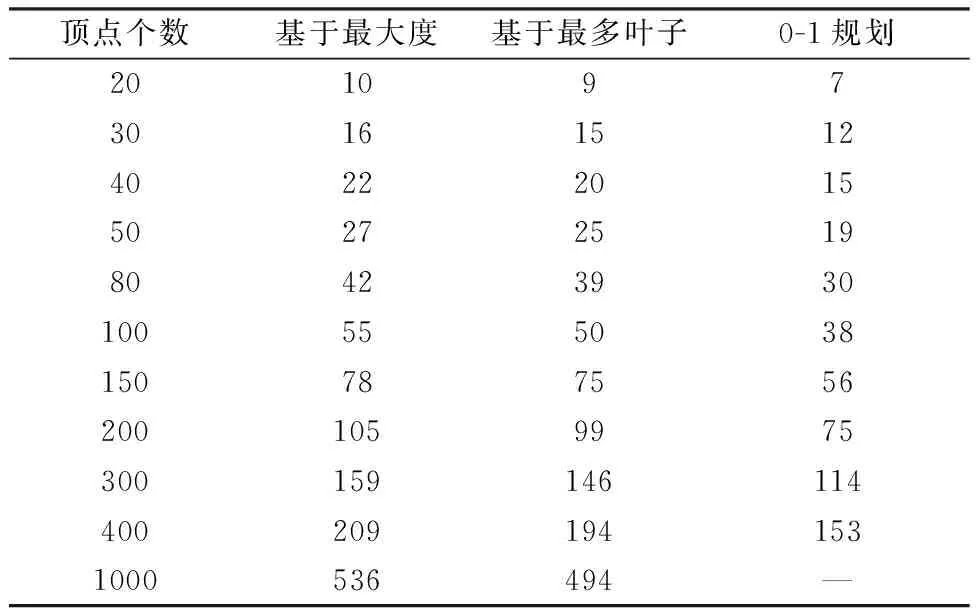
顶点个数基于最大度基于最多叶子0-1规划2010973016151240222015502725198042393010055503815078755620010599753001591461144002091941531000536494—

4 结 语

本文给出了计算树的[1,2]-数的精确算法和两个近似算法,分析了近似算法的计算复杂性并通过实验比较了算法的时间性能和结果的精确性.文献[4]中给出了许多图的不同类型的支配数的算法,其中对于树,很多类型的支配数都有相应的线性算法.因此,对于是否存在计算树的[1,2]-数的线性算法是一个值得深入研究的问题.通过我们的分析,这个问题比文献[4]中的问题复杂得多,因此设计比较好的近似算法也是需要重点研究的问题之一.

[1] BONDY J A, MURTY U S R. Graph theory with applications[M].New York: Macmillan,1976：53-269.

[2] CHELLALI M, HAYNES T W, HEDETNIEMI S T. [1,2]-sets in graphs[J].Discrete Applied Mathematics,2013,161(18):2885-2893.

[3] GUHA S, KHULLER S. Approximation algorithms for connected dominating sets[J].Algorithmica,1998,20(4):374-387.

[4] HAYNES T W, HEDETNIEMI S T, SLATER P J. Fundamentals of Domination in Graphs[M].New York: Marcel Dekker,1998,32-95.

Research on the algorithms of computing the [1,2]-number of trees

ZHANG Chao, ZHAO Chengye

(College of Sciences, China Jiliang University, Hangzhou 310018, China)

A vertex setSof a graphGis a [1,2]-set. Every vertex which is not inSsatisfies that it is adjacent to at least one vertex, but not more than two vertices inS. The [1,2]-number equals the minimum cardinality of a [1,2]-set in G. The algorithms of calculating the [1,2]-number of trees were studied. Firstly, a 0-1 programming model was constructed according to the definition of the [1,2]-number. The exact [1,2]-number of the tree was got by solving the 0-1 programming model. Through star-decomposition of the tree based on the greedy strategy, two approximate algorithms, which calculated the [1,2]-number of trees, were got. Finally, the computing complexity and the performances of the two approximate algorithms were analyzed.

[1,2]-number; 0-1 programming; greedy strategy; approximate algorithm

1004-1540(2015)02-0243-04

10.3969/j.issn.1004-1540.2015.02.022

2015-03-01 《中国计量学院学报》网址：zgjl.cbpt.cnki.net

国家自然科学基金面上项目(No.61173002).

O157.5

A