多采样点下圆度误差最小区域评价方法研究

孟凡良，余晓芬，黄开辉，彭鹏

(合肥工业大学仪器科学与光电工程学院，安徽合肥 230009)

0 前言

圆度误差是指在回转体同一横截面内，被测圆轮廓相对于理想圆的最小变动量，它是零件几何精度的重要指标。能否准确评定圆度误差对保证精密机械零件的质量至关重要。GB/T 7235-2004规定了以下4种圆度误差的评定方法:最小区域法、最小二乘法、最小外接圆法和最大内切圆法。而其中最小区域法是仲裁方法，其他方法均为近似方法［1］。

正因为圆度误差最小区域评价的重要地位，一直以来，国内外学者在这一方面做了大量研究，各种圆度误差最小区域评定算法也应运而生。目前比较具有代表性的算法有:移心法［2］、仿增量算法［3］、搜索法［4］、Voronoi图形法［5］及遗传算法［6］等。近年来，基于CCD或CMOS的图像测量方法在圆度误差测量领域得到了广泛应用。但由于采样点数很多，应用上述算法均无法快速、准确地得到最小区域圆度误差值，因此现阶段计算机一般只输出最小二乘圆度误差值。为了解决多采样点下圆度误差最小区域评价的问题，文中提出一种新的算法，可以准确、高效地获得最小区域圆度误差值。

1 算法要点

圆度误差的最小区域评价［1］指的是:用两个同心圆去包容被测圆轮廓，其中半径差最小的一对同心圆的圆心为最小区域法评定中心，半径差就是最小区域法评定的圆度误差值。而实际评定过程中要依据交叉准则。如图1所示，l为被测圆轮廓，C1和C2为两同心包容圆，半径分别为R1和R2，O为同心圆圆心，a、b、c、d 4个点内外相间地分布于两同心包容圆上满足交叉准则，此时最小区域法评定的圆度误差为R1－R2。

由上述最小区域法判别准则可知:要完成圆度误差的最小区域评价，只需找到被测圆轮廓上满足交叉准则的4点即可。下面将详细介绍文中所提出的新算法是如何通过两步来成功锁定满足交叉准则的4点进而得到最小区域法圆度误差值。

图1 最小区域法评定圆度误差

1.1 “九点法”移心

若将被测圆轮廓看作是一个平面离散点集，则根据圆度误差最小区域评价的定义可得到如下结论:圆轮廓内部所有点中，最小区域圆心的半径极差值(相对于圆轮廓上各采样点距离中的最大值减去最小值)最小。进而可以得到推论:越靠近最小区域圆心的点，其半径极差值越小。根据该推论可以设计算法通过比较半径极差值逐步逼近最小区域圆心，作者通过大量的仿真证明这种逼近虽然有效但却是模糊的，不具有严格的收敛性，尤其当非常接近最小区域圆心时可能会出错，而一旦出错，之后的逼近过程都是无效的。因此提出一种模糊算法——“九点法”，来模糊高效地移心逼近最小区域圆心。

首先，利用最小二乘法算得最小二乘圆心坐标O(x，y)及最小二乘圆度误差值e;其次，以O为中心，以e为边长均布8个点(如图2所示)，认为最小区域圆心一定在这8个点以内;再次，计算这9个点的半径极差值f(1)～f(9)并进行比较:

(1)若f(1)最小，则首先认为最小区域圆心一定在1、2、4、5四点以内，再将f(1)与f(2)、f(4)、f(5)相比较，移心结果如表1。当f(3)、f(7)或f(9)最小时，采用“九点法”移心逼近最小区域圆心的过程类似于1点。

图2 “九点法”移心

表1 f(1)最小时的移心结果

(2)若f(2)最小，则需要先考察1、3、4、6四个点的半径极差值:若f(1)＜f(3)且f(4)＜f(6)，则认为最小区域圆心一定在1、2、4、5四点以内，之后再根据(1)中所述进行移心逼近;若f(3)＜f(1)且f(6)＜f(4)，则认为最小区域圆心一定在2、3、5、6四点以内，再根据(1)中所述进行移心逼近;其他情况时，需要分别在以上两个区域内进行移心逼近，再比较两个区域内移心终点的半径极差值，取其中较小者作为此次移心的结果。当f(4)、f(6)、f(8)最小时，移心逼近的过程类似于2点。

(3)若f(5)最小，则需要先分别比较f(3)、f(6)、f(9)和f(1)、f(4)、f(7)，若前一组中至少有两个分别小于后一组，则认为最小区域圆心一定在1、3、7、9方形区域的上一半，反之一定在下一半;之后再分别比较f(1)、f(2)、f(3)和f(7)、f(8)、f(9)，若前一组中至少有两个点的半径极差值分别小于后一组，则认为最小区域圆心一定在1、3、7、9方形区域的左一半，反之一定在右一半;这样就确定了最小区域圆心所在的范围，进而再根据(1)中所述进行移心逼近。其他情况时，需要分别在4个区域

内进行移心逼近，再比较4个区域内移心终点的半径极差值，取其中最小者作为此次移心的结果。

1.2 根据峰值点群求圆度误差

1.1节中详细介绍了逐步移心逼近最小区域圆心的模糊算法，但毕竟无法得到准确的最小区域圆心，下面将介绍根据峰值点群求取准确的圆度误差的方法。如图3所示，曲线上的各点表示圆轮廓上各采样点与“九点法”移心终点之间的距离，直线l2为最小二乘圆。根据圆度误差最小区域评价的定义，满足交叉准则的4个点只可能出现在曲线上下峰值处。因此考虑设定上下阈值l1、l3来初步划定四点的可能分布区间(①－⑤5个峰值点群)，再穷举所有可能的组合(如①②③④)，逐个验证交叉准则，最终找到4个点并完成圆度误差的最小区域评价。上下阈值l1、l3是根据移心次数在最远峰值点与最小二乘圆之间选择的(如l1至上侧最远峰值点与其至最小二乘圆的距离比为1∶9)，移心次数越多，认为逼近效果越好，阈值就可以越靠近最远峰值点。由于各峰值点群的采样点数相当有限，因此只需利用穷举搜索的方法便能快速准确地得到结果。

图3 根据峰值点群求圆度误差

2 算法的软件实现

图4所示为算法的程序流程图，其给出了算法的具体实现步骤，以下两点需补充说明:

(1)为简化算法，在评定之前需先根据采样点的个数按照近似1/k比例将采样点压缩成100～200个特征点，具体为:若连续k个采样点与最小二乘圆心的距离都大于最小二乘半径，则保留距离最大的采样点，舍去其它k－1个点;若都小于最小二乘半径，则保留距离最小的采样点，舍去其他k－1个点;若既有大于最小二乘半径的又有小于最小二乘半径的，则保留距离最大和距离最小的两个采样点，舍去其他k－2个采样点。

(2)按照算法，在压缩后的100～200个特征点中找到满足交叉准则的4点并获得局点最小区域圆度误差值及此时的评定中心O'。之后在原采样点中锁定这4个点(两个内圆上的点，两个外圆上的点)，分别以该四点为中心取k邻域，考察邻域内各点与圆心O'的距离:若以内圆点为中心，则取距离最小者;若以外圆点为中心，则取距离最大者。依据重新确定的四点坐标，即可得到全点最小区域圆度误差值。

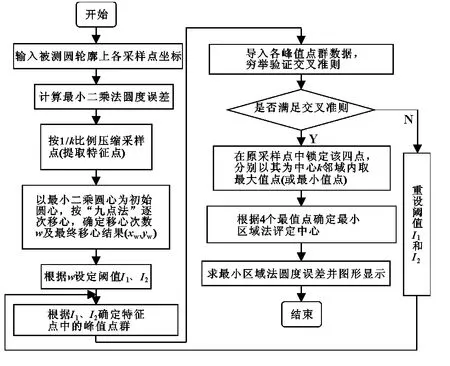
图4 算法程序流程图

3 仿真及实验

为验证算法的正确性、可靠性及快速性，作者借助Matlab进行了一系列的仿真。根据傅里叶变换的理论，认为实际圆轮廓为各阶谐波叠加的结果［7］，在极坐标下构建被测圆轮廓的数学模型:

式中:r0为圆半径理论值(直流分量);

ai为第i次谐波分量幅值;

φi为第i次谐波分量相位;

random为随机误差值。

理论上，只要采样点数足够，测得的离散点坐标数据就包含了实际圆的所有加工误差特征(谐波特征)，又在实际生产加工中一般不会出现高次谐波分量［8］(ai≥0.05μm，则i≤6)。基于以上分析，根据直流分量r0选取合适的ai及φi值，随机误差取值均为0～1/8 000 mm，可以构建多组圆轮廓，保持1 500个采样点及1/15的压缩比例不变，代入程序进行仿真，仿真的结果及程序运行的时间如表2所示。经验证，表2中全点最小区域圆度误差值确为对圆轮廓上1 500个采样点的最小区域评价真值;因为采样点数很多，若采用已有的移心法或迭代法等，程序运行效率将很低［9］。

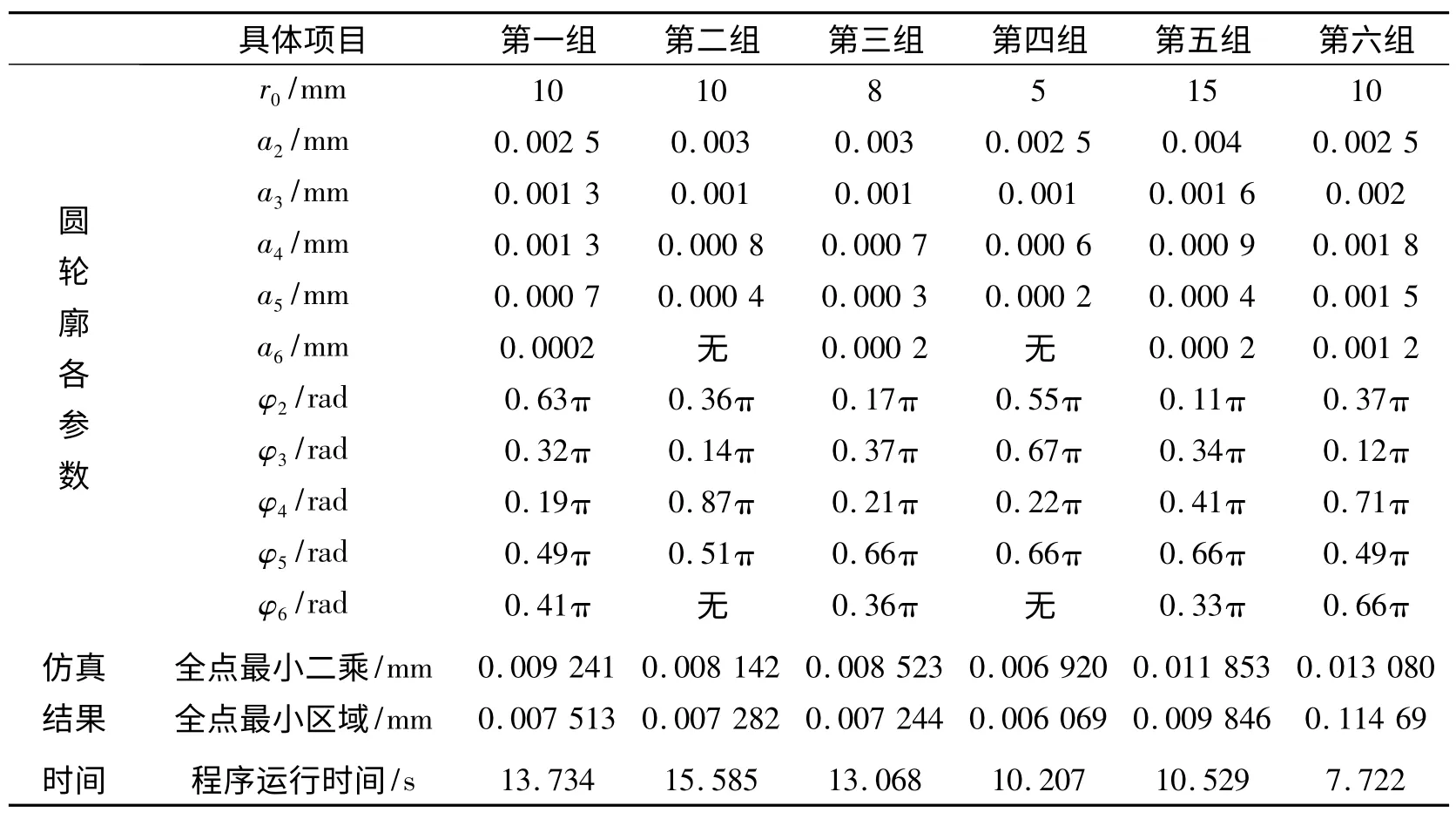
表2 输入参数及仿真结果

图5所示为第一组仿真中三次移心的过程，易见移心距离逐次递减且移心终点确与最小区域圆心非常接近。如1.2节中所述，根据移心次数(w=3)设定上下阈值(至最远峰值点与其至最小二乘圆的距离比均为1∶9)，确定各峰值点群后找到满足交叉准则的四点并求取局点最小区域圆度误差值。图6给出特征点与各圆心的距离曲线，其中特征点与移心终点的距离曲线和特征点与最小区域圆心的距离曲线几乎重合，再次证明了“九点法”移心的有效性。

图5 “九点法”逐次移心

图6 特征点与各圆心距离曲线(1)

为验证算法的高效性及实用性，作者采用自行研制的多功能非接触式圆度仪(如图7所示)，利用基于CCD的图像测量手段对一φ10 mm的无油滑动轴承的外圆轮廓(Talyrond 365型圆度仪测得最小区域圆度误差值为17.09μm)进行了圆度误差的测量。首先采用型号为Guppy Pro F-201B的工业相机对被测工件进行图像采集，如图8所示:其次完成数字图像的处理，提取外圆的边缘轮廓并输出圆轮廓上各采样点的坐标值(约2 200个采样点);最后将坐标值带入程序，运行11.454 s后输出结果如表3所示。图9给出122个特征点相对于最小二乘圆心、移心终点及最小区域圆心距离的3条曲线。由3条曲线的重合度可见“九点法”移心逼近的效果是明显的;而短时间内在各峰值点群中锁定满足交叉准则的4个点证明该算法可以实现多采样点下圆度误差的最小区域评价，具有一定的实用性。

表3 实验结果

图7 多功能非接触式圆度仪

图8 被测环形轴套零件

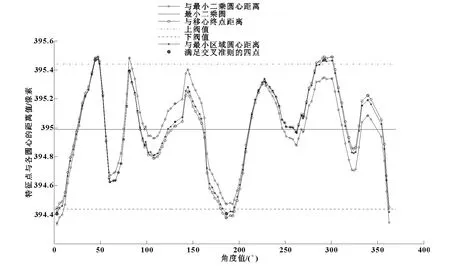
图9 特征点与各圆心距离曲线(2)

4 结论

提出了一种应用于多采样点下的圆度误差最小区域评价算法，一定程度上填补了该领域的空白，为圆度误差的精确评定提供了新的思路。对该算法进行了详细的介绍，并通过大量的仿真及实验验证了其正确性、可靠性和高效性。该算法的原理易于理解，便于实现计算机编程，具有极强的通用性，可广泛地应用于圆度仪、机器视觉测量等多采样点的情况。

［1］徐志玲，刘宇，程琦．4种圆度误差评定方法分析［J］．计量学报，2009，30(5A):38－41．

［2］方沁林．圆度误差评定的算法研究与软件设计［D］．武汉:华中科技大学，2007:29－37．

［3］岳武陵，吴勇．基于仿增量算法的圆度误差快速准确评定［J］．机械工程学报，2008，44(1):87－91．

［4］张春阳，雷贤卿．基于几何优化的圆度误差评定算法［J］．机械工程学报，2010，46(12):8－12．

［5］张铁英，来可伟．计算几何评定圆度的方法研究［J］．工程图学学报，2002(3):145－153．

［6］CUI Changcai，CHE Rensheng．Circularity Error Evaluation Using Genetic Algorithm［J］．Optics And Precision Engineering，2001，9(6):499－505．

［7］黄富贵，董兆鹏，崔长彩．用谐波分析方法识别零件的圆度误差特征［J］．实验室研究与探索，2011，30(8):8－14．

［8］蒲竞秋．基于谐波分析的误差分析方法［C］//四川省电子学会电子测量与仪器专委会2005年学术年会论文集，2005:18－23．

［9］薛玉君，畅为航，雷贤卿，等．圆度误差评定的研究与展望［J］．机床与液压，2008，36(12):183－185．