带有对流项和源项的非线性交叉扩散方程组的不变子空间及其分类

屈改珠

（渭南师范学院数学与信息科学学院，陕西渭南714000）

带有对流项和源项的非线性交叉扩散方程组的不变子空间及其分类

屈改珠

（渭南师范学院数学与信息科学学院，陕西渭南714000）

利用不变子空间方法研究带有对流项和源项的非线性交叉扩散方程组，借助符号计算系统Maple确定出方程组所容许的多项式不变子空间×中的完全分类，进一步将方程组约化为有限维动力系统并构造了方程组的广义分离变量解。

不变子空间；非线性交叉扩散方程组；广义分离变量解

非线性问题大多可以用微分方程包括非线性演化方程（组）来描述和刻画。这类方程的精确解对于解释和描述一些自然现象或发现自然现象的新规律具有重要意义，同时构造求解方程的过程，往往会产生新的数学思想、方法和理论。因此，寻求和构造非线性演化方程（组）的精确解成为数学和物理工作者的重要研究课题之一。

不变子空间方法是和条件Lie－Bäcklund对称方法以及微分约束方法相关的一种求解非线性演化方程（组）的有效方法。该方法由Galaktionov［1］首次提出，并利用不变子空间方法研究带有二次非线性项演化方程的广义分离变量解。文献［2］进一步推广了不变子空间方法，并将其成功应用于非线性交叉扩散方程组的分类。事实上，许多非线性演化方程（组）的精确解都可以由不变子空间方法得到［3－8］。

本文利用不变子空间方法研究带有对流项和源项的非线性交叉扩散方程组

其中f（u，v）、p（u，v）、h（u，v）、r（u，v）、g（u，v）、q（u，v）、l（u，v）、s（u，v）都是u和v的待定函数。方程组（1）可以被看作是带有对流项和源项的非线性扩散方程

的推广形式，在物理和生物中具有很多应用，对于方程（2）已有很多研究结果。文献［9］运用不变集理论得到了一般的非线性扩散方程ut＝A（u）uxx+ B（u）u2x+C（u）的泛函分离变量解。文献［10］运用二阶条件Lie－Bäcklund对称构造出方程（2）中反应系数为幂函数的非古典解。

1 不变子空间理论

考虑非线性演化方程组

其中U＝（u1，u2，…，um）∈Rm，

Fq（·）是充分光滑函数。如果向量微分算子F满足条件

即

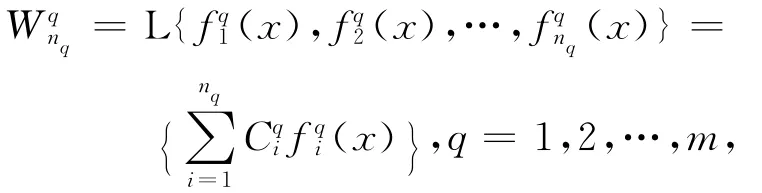
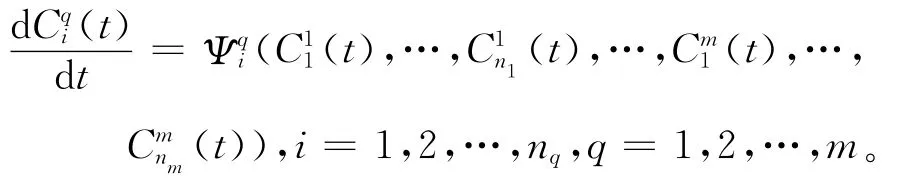
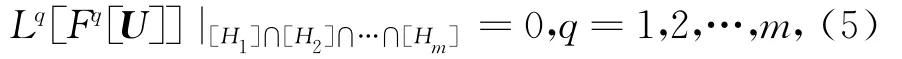
其中［Hq］表示方程Lq［uq］＝0，q＝1，2，…，m及其关于x的微分结果。由不变条件（5）可以确定出不变子空间理论中重要的维数定理［2］。

定理1 令F［U］是一个k阶非线性向量微分算子，且容许不变子空间×，如果F1，u2≠0，F2，u1≠0，同时0＜n2≤n1，则有n1－n2≤k，n2≤3k+1，或n1－n2≤k，n1≤4k+1。

2 方程组（1）的分类结果

这一部分将利用不变子空间方法研究方程组（1）在它所容许的多项式型不变子空间中的分类，并构造相应的精确解，即向量微分算子（F1，F2）容许多项式不变子空间×，其中×由以下线性常微分方程组定义：

由定理1，将对（n1，n2）分别讨论以下情况：

（9，8），（9，7），（8，7），（8，6），（7，6），（7，5），

（6，5），（6，4），（5，5），（5，4），（5，3），（4，4），

（4，3），（4，2），（3，3），（3，2），（2，2）。

首先，假定向量微分算子（F1（u，v），F2（u，v））容许多项式型不变子空间W19×W28，即

则相应的不变条件为

将算子F1［u，v］、F2［u，v］代入到方程（8）和（9）中并合并同类项，它们的左端都成为关于ui（i＝1，2，…，8）及vj（j＝1，2，…，7）的多项式。其中，在方程（8）中，比较u8u3、v7v4、u8v3和u7v4前的系数，得到

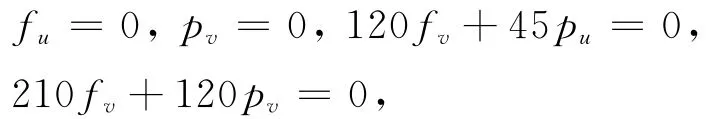
所以f（u，v）和p（u，v）都是常数。将此结果代入到方程（8），比较u8u2、u8v2、v7v3以及u8v1、u8u1、v7v2的系数，有

因此h（u，v）和r（u，v）关于u和v是线性的。对不变条件（9）进行同样的分析，也可推出g（u，v）、q（u，v）是常数，l（u，v）、s（u，v）都是u、v的线性函数。所以，得到下面的定理。

定理2 没有带有交叉扩散对流项的非线性微分算子（F1（u1，v），F2（u，v））容许由常微分方程组（7）定义的多项式型不变子空间W19×W28。

当（n1，n2）取其他情况时，对不变条件（5）进行同样的分析和计算，得到下面的结论。

定理3 没有带有交叉扩散对流项的非线性微分算子（F1（u，v），F2（u，v））容许由下面的常微分方程组（6）定义的多项式子空间×，其中（n1，n2）＝（9，7），（8，7），（8，6），（7，6），（6，5），（5，5）。

定理4 如果（n1，n2）＝（8，6），（7，5），（6，4），（5，4），（5，3），（4，4），（4，3），（4，2），（3，3），（3，2），（2，2），则非线性向量微分算子（F1［u，v］，F2［u，v］）及其他所容许的多项式不变子空间×可以被表示成如下的形式：

下面给出一个具体求解的例子进行说明。

例1 在（19）式中，令c9＝c10＝c18＝d18＝d22＝1，ci＝0，i≠9、10、18，di＝0，i≠18、22，则方程组（1）变为

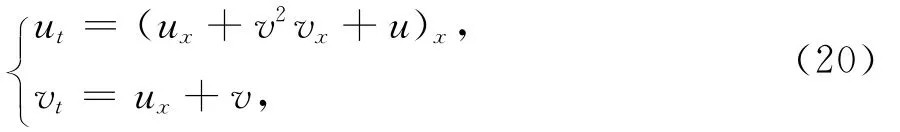
它在子空间W12×W22中有多项式型解，即

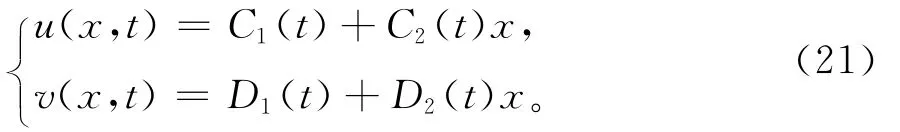
将它们代入到方程组（20）中，将方程组约化为有限维动力系统：

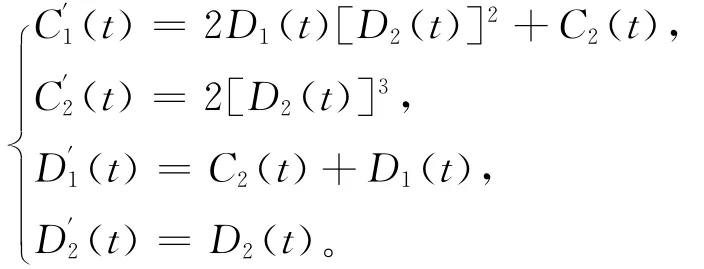
求解此方程组，得到方程组（20）的广义分离变量解

其中ai、bi（i＝1、2）为任意常数。

3 结论

本文讨论了带有对流项和源项的非线性交叉扩散方程组（1）在由常微分方程组（6）所确定的多项式不变子空间×中的完全分类，从而将方程组约化为有限维动力系统并构造了方程组的广义分离变量解。值得一提的是，文献［11］利用不变子空间方法构造了分数阶微分方程的精确解。因此，下一步将考虑利用不变子空间方法对分数阶微分方程组进行分类及求解。

［1］Galaktionov V A.Invariant subspaces and new explicit solutions to evolution equations with quadratic nonlinearities［J］.Proceedings of the Royal Society of Edinburgh：Section A Mathematics，1995，125：225－246.

［2］Qu Changzheng，Zhu Chunrong.Classification of coupled systems with two－component nonlinear diffusion equations by the invariant subspace method［J］.Journal of Physics A：Mathematical and Theoretical，2009，42：475201.

［3］Svirshchevskii S R.Lie－Bäcklund symmetries of linear ODEs and generalized separation ofvariables in nonlinear equations［J］.Physics Letters A，1995，199：344－348.

［4］Galaktionov V A，Svirshchevskii S R.Exact solutions and invariant subspaces of nonlinear partial differential equations in mechanics and physics［M］.London：Chapman and Hall／CRC，2007.

［5］Ma Wenxiu.A refined invariant subspace method and applications to evolutionequations［J］.Science China Mathematics，2012，55：1769－1778.

［6］Zhu Chunrong，Qu Changzheng.Maximal dimension of invariant subspaces admittedby nonlinear vector differential operators［J］.Journal of Mathematical Physics，2011，52：043507.

［7］Zhu Chunrong.Second－order nonlinear differential operators possessing invariant subspaces of submaximal dimension［J］.Chinese Physics B，2011，20：010201.

［8］Qu Gaizhu，Zhang Shunli，Li Y L.Third－order nonlinear differentialoperators preserving invariant subspaces of maximal dimension［J］.Chinese Physics B，2014，23：110202.

［9］Qu Changzheng，Estevez P G.Extended rotation and scaling groups fornonlinear evolution equation［J］.Nonlinear Analysis：Theory，Methods and Applications，2003，52：1655－1673.

［10］Ji Lina，Qu Changzheng.Conditional symmetries and solutions toa class of nonlinear diffusion convection equation［J］.Communications in Theoretical Physics，2006，46：668－674.

［11］Gazizov R K，Kasatkin A A.Construction of exact solutions forfractional order differential equations by the invariant subspace method［J］.Computers and Mathematics with Applications，2013，66：576－584.

〔责任编辑 宋轶文〕

Invariant subspaces and classification to systems of nonlinear cross－diffusion equations with convection and source terms

QU Gaizhu
（School of Mathematics and Information Science，Weinan Normal University，Weinan 714000，Shaanxi，China）

The invariant subspace method is extended to investigate systems of two－component nonlinear cross－diffusion equations with convection and source terms.Based on the symbolic computation system Maple，a complete classification of the invariant subspace×are derived. As a result，the systems are reduced to finite－dimensional dynamical systems and the corresponding explicit solutions are constructed.

invariant subspace；nonlinear cross－diffusion equations；generalized separation of variables solution

35A22，35A25，35K55

2014－12－27

陕西省教育厅基金（14JK1246）；渭南师范学院理工类科研项目（15YKS005）；渭南师范学院校级特色学科建设项目（14TSXK02）

屈改珠，女，讲师，博士，主要研究方向为偏微分方程。E－mail：qugaizhu.hi＠163.com

O175.2

：A

1672－4291（2015）05－0004－05

10.15983／j.cnki.jsnu.2015.05.152