巧用数形结合 提升教学智慧——一道课标习题的教学与思考

钱建华 (通州区兴仁中学 江苏南通 226371)



巧用数形结合 提升教学智慧
——一道课标习题的教学与思考

钱建华 (通州区兴仁中学 江苏南通 226371)

《义务教育数学课程标准(2011年版)》(下称《课标》)指出：在数学课程中，应当发展学生的几何直观.而几何直观教学的关键点是能够运用形象的几何图形解决复杂的数学问题，这里就蕴涵了一个重要的数学思想——数形结合.伟大的数学家华罗庚对数形结合在学习数学中的作用作了这样的阐述：“数与形本是相倚依，焉能分作两边飞，数缺形时少直观，形少数时难入微，数形结合百般好，隔裂分家万事非，切莫忘，几何代数统一体，永远相联系，切莫分离.”这段分析精辟地阐述了数与形之间的密切关系和相互作用.下面笔者以一道《课标》习题的教学为例谈谈个人的一点思考，以求抛砖引玉.

1 问题再现

《课标》课程内容及实施建议中的实例第79例：利用几何图形研究代数问题.

例1[1]对于给定的2个数x和y，求使得(x-b)2+(y-b)2达到最小的b，也就是说要找到一个b0，使得对任意的b有

(x-b0)2+(y-b0)2≤(x-b)2+(y-b)2.

(此题作为前一天的作业布置给学生，要求学生思考并尽量完成.)

2 解法探究

2.1 代数方法

生1：我用了“列举法”，先取x=2,y=3，得

(x-b)2+(y-b)2=(2-b)2+(3-b)2=

2b2-10b+13=

师：不错，课后认真思考过！但有个问题，仅取了3组数得到的结论能说明其正确性吗？是否有以特殊代替一般，以偏概全之嫌？

生：……

(x-b)2+(y-b)2=

(x-b0+b0-b)2+(y-b0+b0-b)2=

(x-b0)2+(y-b0)2+

2[(x-b0)+(y-b0)](b0-b)+

2(b0-b)2,

(x-b)2+(y-b)2=(x-b0)2+(y-b0)2+

2(b0-b)2，

而(b0-b)2≥0，于是

(x-b0)2+(y-b0)2≤(x-b)2+(y-b)2.

师：很好！能想到这一点说明你数学基本功非常扎实.但如何想到这一方法呢？

师：此方法是有它的特殊性，一般不容易入手，其他同学有更好的方法吗？

2.2 数形结合

(见学生个个眉头紧锁)师生一起回忆关于两点间的距离、平面直角坐标系、直线的学习，教师引导学生走向数形结合(经过思索、提示、讨论后见学生思维还是没跟上).

师：我们不妨先来解决例2.

例2 如图1,点A的坐标为(-1，0)，点B在直线y=x上运动，当线段AB最短时，点B的坐标为

( )

(2012年四川省广元市数学中考试题)

生4：选B.

师：你能说说为什么吗？

图1 图2

生4：如图2，过点A作AB′⊥OB，垂足为点B′，过点B′作B′C⊥x轴，垂足为C.由垂线段最短可知，当B′与点B重合时，AB最短.因为点B在直线y=x上运动，所以△AOB′是等腰直角三角形，△B′CO也是等腰直角三角形.又因为点A的坐标为(-1，0)，所以

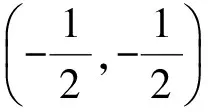
师：非常好！同学们发现此题和例1之间的联系了吗？由此能想到解题思路吗？

生5：如图3，可以把给定的2个数看作数对，对应于坐标平面内的点，用A(x,y)表示.对于任意数b也可以看作数对(b,b)，用点B(b,b)表示.易知点B(b,b)是在经过原点、与横坐标轴所交锐角为45°的直线上.这样本题就变为：在这条直线上找一点，使得这一点到给定点A(x,y)的距离最短.根据“直线外一点与这条直线上各点的所有连线段中，垂线段最短”，这一点应当是点A(x,y)到直线的垂足，设其为B′(b0,b0),则

AB′2=(x-b0)2+(y-b0)2.

师：一点就通，跟老师想的完全一样！生5受到例2的启发，巧妙地将此代数问题转化成了几何问题！实际上，利用直角坐标系，不仅能够推导出几何图形的代数表达式，还能够利用几何图形来研究代数问题，这充分体现了数形结合的重要思想.

2.3 拓展延伸

2.3.1 从特殊到一般的延伸

师：如果将例1改成：对于给定的2个数x和y，求使得(x-b)2+(y-a)2达到最小的b.那又该如何解决呢？请同学们小组讨论后交流.

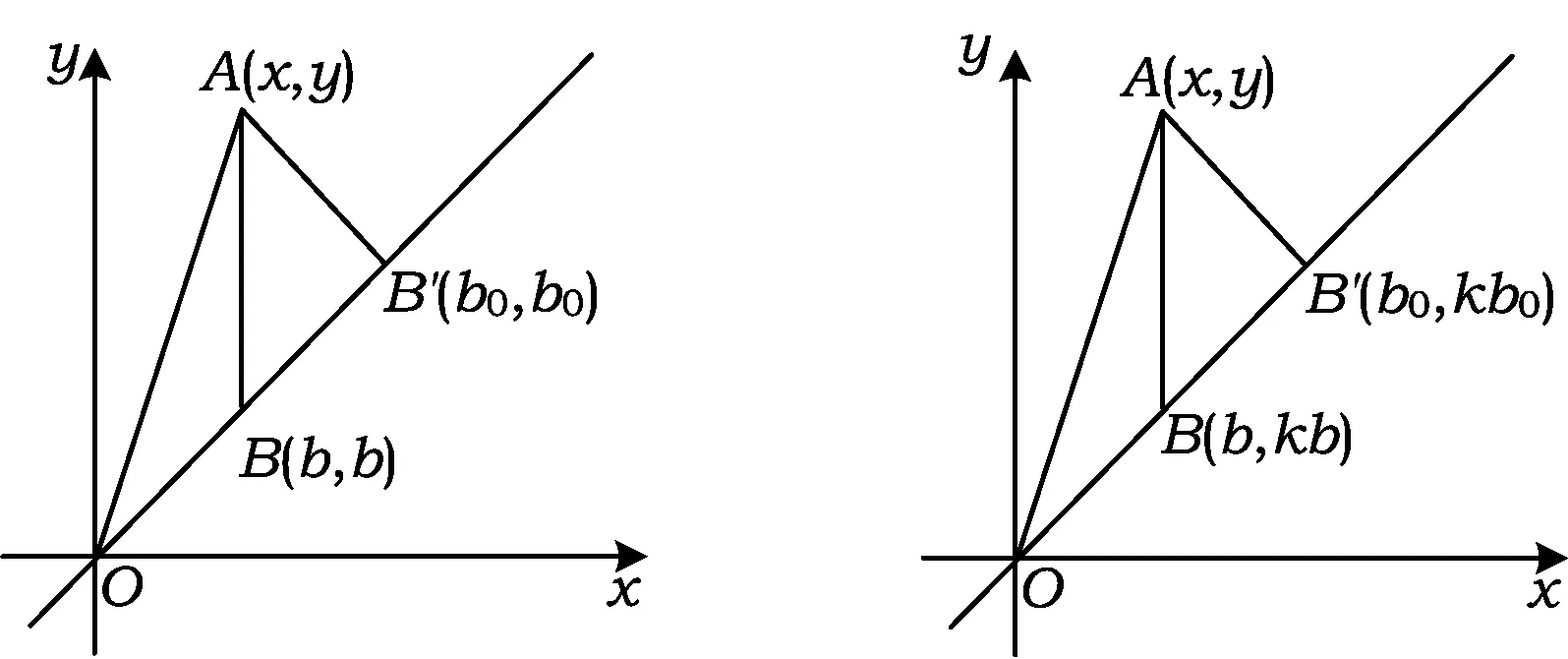
图3 图4

生6：可设a=kb，题目即变成要求使得(x-b)2+(y-kb)2达到最小的b.如图4，仍然利用直角坐标系，可得

从而

第二，从形成审计结论所需要的审计证据来看，审计证据的来源不仅仅包括审计对象的财务信息，还包括审计人员通过审计程序获取的非财务信息。另外，审计人员在审计过程中通过合理推断得到的结论以及审计人员从供应商、销售商等方面获得的外部资料和凭证也是审计证据的重要组成部分。

AB′2=(x-b0)2+(y-kb0)2.

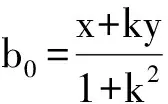
师：太好了，能触类旁通！我们已经能够解决一般情况，熟悉利用数形结合解决这种最值问题.其实这种最值问题和统计与概率也紧密相连，我们来了解一下.

2.3.2 从“最值问题”到“统计与概率”的延伸

3 教后思考

3.1 加强教学预设

笔者通过批阅学生作业发现学生对此问题存在疑惑，有些学生甚至根本无从下手，于是笔者在教学时没有急于直接向学生讲解，而是先让学生思考、讨论，合作分析，发挥集体智慧，然后“反其道而行之”，再插入“引例”，为解决问题铺好道路，进而引发了学生对于问题的思考.正如预设那样，有了“数形结合”，顺利得到“智慧”的“生成”.苏霍姆林斯基在讲“如何获取知识”时说过：“在我看来,教给学生能借助已有知识去获取知识,这是最高的教学技巧之所在.”课堂教学总是在“预设”与“生成”间交融进行的，教师应在了解学情的基础上加强教学预设，对可能出现的问题尽可能地预设解决措施，引导学生的思维逐步步入正轨.学生从接触问题到解决问题有一个较长的过程，这是由学生的认知水平和问题本身的难度所决定的.教师要明了其间的巨大落差，给学生充分的思考与讨论时间，在原有认知和现存问题之间合理设置阶梯，架设桥梁，帮助学生搭建解决问题的“脚手架”，让学生“跳一跳，就能摘到桃子”，在“最近发展区”不断完善自己的认知水平，提升思维品质[2].

3.2 注重数形结合

解决本题的关键就是“数形结合”，数形结合的重点就是代数问题几何化，也就是“以形解数”.在解题中，对于解决抽象的“数”的问题，可充分挖掘其条件的几何意义，进而构造数轴、平面直角坐标系、三角形、四边形、圆等几何图形并利用它们的有关性质、定理，借助“形”的直观进行解题，不仅可使问题获得避繁就简、化难为易的新颖解法，而且能避免复杂的计算与推理，同时对创造性思维的开发与培养也很有益处.因此，在教学中要注意培养学生数形结合意识，争取做到胸中有图、见数思图，学会从“数”和“形”2个角度思考和解决问题，这也是帮助学生建立几何直观的极为有效的途径之一.数形结合不仅能培养和发展学生的空间观念及几何直观能力，而且能培养学生形象思维与抽象思维的交叉运用，从而有助于培养学生灵活运用知识的能力.

3.3 适当拓展延伸

首先，在教学中，适当地对问题进行拓展延伸、借题发挥，就是让学生在已解决问题的基础上进一步看清实质，根据问题中的条件与结论进行再探究的过程，是一个思维提升的过程；其次，学习数学就应该理解其本质、掌握其方法与规律，从而做到会一题通一类；再次，对问题的拓展延伸，能让学生认识问题的数学本质，归纳出每一类题的特征，这样在独立解题时才能得心应手，真正提高数学能力.

总之，在数学教学中巧妙地运用数形结合的思想方法解决一些类似于本例的抽象代数问题，可以起到事半功倍的效果，适时、适当地对问题进行拓展延伸有助于学生思维层次的提升.我们不仅要提升学生的学习智慧，而且要提升教师的教学智慧.

[1] 中华人民共和国教育部.义务教育数学课程标准[M].北京:北京师范大学出版社，2012:126-127.

[2] 钱建华.注重方法形成过程 促进课堂智慧生成[J].中学教研(数学),2014(11)：28-30.