锥形PDC齿破岩机理仿真研究

豆宁辉，杨顺辉

（中国石化石油工程技术研究院，北京100101）

锥形PDC齿破岩机理仿真研究

豆宁辉，杨顺辉

（中国石化石油工程技术研究院，北京100101）

锥形PDC齿作为一种新型破岩方式，其相关理论在国内研究还处于起步阶段。采用DruckerPrager准则，以等效塑性应变作为破坏准则，建立了基于ABAQUS的锥形PDC齿切削岩石有限元分析模型。通过数值仿真、理论分析阐述了锥形PDC齿切向上以剪切破坏为主、侧向方向以挤压拉伸断裂破坏为主的破岩机理，以及“相邻”效应，并且数值仿真分析了切削深度、切削角度对锥形PDC齿破岩效率的影响规律，优选出最优切削角度20°。研究结果对锥形PDC齿为基础的新型PDC钻头的设计提供了依据。

锥形PDC齿；破岩机理；数值仿真；切削角

在复杂地质条件下的油气钻探工作中，经常钻遇碳酸盐岩、火成岩等难钻地层，其强度高，硬度大，可钻性差，研磨性强。现有破岩工具会存在钻头寿命短、钻井周期长等问题。Simth钻头公司2014年推出了基于锥形PDC齿为基础的StingBlade钻头，与常规PDC切削齿相比，其抗冲击强度更大；随着机械钻速的增加，Stinger切削齿钻头的转矩平均减少了26%；Stinger切削齿比PDC切削齿有着更加平衡的切削响应，StingBlade钻头在全球300多口井中进行了成功应用，总作业进尺已超过209 095 m（686 000英尺）。中国石油大学（华东）2014年进行了锥形PDC齿钻头的研制及室内试验评价［1-2］，但其破岩机理的理论研究尚不完善，笔者利用仿真研究方法分析了切削深度、切削角度对锥形PDC齿破岩效率的影响规律，以优选锥形PDC齿最优切削角度。通过对锥形PDC齿破岩机理与规律的研究，为新型PDC钻头的研制提供一定的理论依据。

1　锥形PDC齿破岩机理

锥形PDC齿作为一种新型石油钻井破岩工具，既不同于牙轮钻头的冲击破岩，也不同于PDC钻头的剪切破岩。其破岩方式是在轴向力和转矩共同作用下连续旋转破岩，特殊之处在于锥形PDC齿是以前倾角的角度将岩石“犁”出沟槽，在切向方向将岩石从母体上剥离，同时在侧向方向对岩石产生挤压破坏作用。

2　建立有限元模型

2.1优选有限元分析软件

ABAQUS作为最先进的大型通用有限元分析软件之一，能够解决从相对简单的线性分析到许多复杂的非线性问题，尤其是它的非线性力学（几何、材料、接触）分析功能具有世界领先水平，广泛应用于机械、化工、土木等各领域的工业设计中。

岩土介质是具有非均质、非线性以及几何形状的任意性、不连续性等因素的特殊介质。ABAQUS能够提供岩土工程分析中常用的本构模型，如弹性和非线性弹性模型，MohrCoulomb模型，修正的DruckerPrager模型。

鉴于上述ABAQUS的强大功能，本文选择ABAQUS作为锥形PDC齿破碎岩石有限元分析模型的平台。

2.2模型假设

1） 将岩石看作各向同性介质，弹塑性体，不考虑围压、温度、钻进液等对岩石的影响。

2） 不考虑锥形PDC齿的磨损，锥形PDC齿与岩石的接触部分为聚晶金刚石，硬度极大，视为刚性体。

3） 锥形PDC齿实际绕一定大小的旋转半径螺旋吃入地层，但螺旋角很小，所以将锥形PDC齿的运动简化为平面直线运动，且在破岩过程中，切削速度和切削深度都固定不变。

2.3几何模型建立与网格划分

2.3.1岩石

1） 几何模型。岩石建为长方体模型，尺寸为30 mm×20 mm×10 mm。

2） 网格划分。综合考虑计算量、计算时间以及计算精度，将岩石划分为上下两部分，与锥形PDC齿接触的上部网格划分较密，大小为0.5 mm，下部较疏，为1 mm，两部分单元均采用C3D8R（8节点六面体线性减缩积分单元），使用结构网格划分技术（Structured），最终共划分38 400个C3D8R单元，如图1所示。

图1　岩石和锥形PDC齿几何模型

2.3.2锥形PDC齿

1） 几何模型。锥形PDC齿设为锥顶半径2.5 mm，锥角85°，锥齿直径14 mm，总高20 mm。

2） 网格划分。锥形PDC齿分为锥顶和其余部分，分别进行网格划分。锥顶部分，网格大小设为0.2mm，采用C3D4单元和自由网格划分技术（Free）；其余部分网格大小设为0.5 mm，采用C3D8R单元和扫略网格划分技术（Sweep），最终锥形PDC齿共划分44 875个网格单元，如图1所示。

2.4材料模型选取

本模型主要考虑岩石的损伤与破坏，所以将锥形PDC齿约束为刚性体，设置密度为7 800 kg／m3，弹性模量为200 GPa，泊松比为0.2。

本文采用典型砂岩的力学参数作为有限元模型中岩石的参数。岩石视为弹塑性体，弹性阶段，采用线弹性本构模型；塑性阶段采用DruckerPrager准则，并以等效塑性应变作为岩石破坏准则［3］，材料参数如表1所示。

表1　岩石材料属性

2.5定义分析步

采用动态显示分析模拟锥形PDC齿破岩过程。显示分析不仅能够模拟复杂的接触，而且相比于隐式分析需要更小的时间增量步，不需要迭代和收敛准则。

本文将模拟时间设置为0.05 s，并设置相关场变量和历史变量输出。

2.6边界条件

对岩石底部进行PINNED约束；对锥形PDC齿的参考点施加x方向的恒定速度，并约束其他5个自由度，如图2所示。

图2　模型边界条件

参考实际钻头上切削齿的线速度，将锥形PDC齿的线速度定为0.5 m／s。

2.7定义接触相互作用

接触属性中接触对的法向行为法则采用Hard Contact，切向行为法则采用库伦摩擦模型，摩擦因数设为0.3。

接触采用ABAQUS／Explicit模块中的General Contact，并在Input文件中将接触双方改为锥形PDC表面以及岩石内部所有可能接触的单元。

3　仿真结果分析

3.1岩石受力分析

本文利用锥形PDC齿破岩有限元模型，首先模拟了锥形PDC齿以15°前倾角、2mm切削深度下破坏岩石的过程。图3～5分别为同一时刻岩石与锥形PDC齿接触部分应力云图、岩石切向应力云图、岩石侧向应力云图。

图3　锥形PDC齿前岩石应力云图

图4　岩石切向应力云图

图5　岩石侧向应力云图

从以上岩石应力云图可以看出：

1） 锥形PDC齿顶部正下方有一处应力最大区，整体形状为椭球形。

2） 沿锥形PDC齿运动方向切向上，有两处应力最大区，分别位于锥形PDC齿正前方偏两侧，并且齿前方应力等值线层抛物线形状；岩石上表面破碎形状为“∧”形，表明锥形PDC齿在切向上对岩石产生“犁削”作用。

3） 锥形PDC齿两侧各有一处应力最大区域。

4） 锥形PDC齿产生的破碎带侧向截面呈“V”形。“V”形底部宽度为3 mm，和锥形PDC齿正前方与岩石上表面接触宽度相同；“V”形上部宽度为6 mm，是接触宽度的两倍，说明锥形PDC齿两侧对岩石产生了挤压破坏作用。

根据以上数值仿真对锥形PDC齿破岩作用的分析，本文综合弹性力学、断裂力学，并借鉴盘形滚刀、镐形截齿等破岩工具的破岩机理模型［4-8］，对锥形PDC齿的犁削破岩机理在切向、侧向以及“相邻效应”作出如下阐释。

3.2切向破岩机理分析

根据数值仿真结果，将锥形PDC齿的破岩过程分为变形及裂纹起裂、密实核形成、裂纹扩展及块体崩落4个阶段。

1） 变形及裂纹起裂阶段。

如图6所示，当锥形PDC齿作用于岩石时，锥形PDC齿与岩石之间会产生挤压效应，在锥顶前下方出现生压缩区，同时沿切削力方向一定深度处（深色部分）产生最大拉应力。在此阶段，锥形PDC齿边缘部分岩石在压应力作用下开始破坏，内部拉应力区的拉应力达到岩石抗拉强度，产生局部破坏，形成初始裂纹。

图6　变形及裂纹起裂阶段

2） 密实核形成阶段。

如图7所示，随着位移载荷的增加，齿前下方压缩区岩石首先发生破碎，并被锥形PDC齿挤压，形成密实核。

图7　密实核形成及裂纹扩展阶段

3） 裂纹扩展阶段。

随着位移载荷的增加，密实核作为传力介质向周围岩石施加压力，产生拉伸应力。内部裂纹沿最大拉应力方向向自由面扩展，如图8所示。

图8　裂纹扩展阶段

4） 宏观破裂阶段。

随着载荷的进一步增加，内部裂纹与自由面迅速贯通，产生宏观破裂，完成一次破坏过程。宏观破裂形态如图9所示。随后，锥形PDC齿再次与岩石接触，形成压应力区，开始下一个破坏过程［9-10］。

图9　岩石宏观破裂形态

3.3侧向破岩机理分析

锥形PDC齿前部在剪切破岩的同时，两侧对岩体也会产生挤压作用，尤其是密实核形成后，挤压作用增加，两侧出现拉伸裂纹，随着锥形PDC齿载荷的增加，拉伸裂纹主要向两侧自由面和水平方向扩展，最终产生破坏［11-13］，如图10所示。

图10　锥形PDC齿侧向破岩模型

3.4“相邻”效应分析

多个锥形PDC齿同时破岩过程中将会产生“相邻”效应［15-16］：一方面侵入相同深度所需的切削力比单齿要变小一些，另一方面侧向裂纹的发展将沿着相邻两切槽间最短的直线距离发展。裂纹是否贯通与切削齿间距、切削深度或切削力、切削齿顶部本身结构参数有关。即使裂纹不能贯通产生岩块，相邻切削齿产生的岩脊再次被切削时也会很容易破碎。如图11。

图11　“相邻效应”示意

3.5切削角对破岩效率影响分析

为研究切削角度在不同切削深度下对锥形PDC齿破岩效率的影响规律，本文制定如下模拟方案，如表2所示。

根据数值仿真方案，共模拟6种切削深度、6种切削角度下36种切削状态。破岩过程如图12所示。

本文通过计算破碎单位体积岩石所需要的能量，即破岩比能，来比较不同切削深度、切削角度下锥形PDC齿的破岩效率。破岩比能越小，破岩效率越高，反之，破岩效率越低。

表2　数值仿真方案

图12　破岩过程

破岩能量可以通过破岩过程中的能量曲线读取，如图13所示，或者在XY Data选项中提取最后时刻破岩能量值；破岩体积通过计算失效单元的体积和得到，最终计算两者的比值得到每种切削状态下的破岩比能，如图14～15所示。

从图14～15可以得出如下结论：

1） 破岩比能随着切削角度的增加，先减小后增加，从小到大排列依次为20、15、10、25、5、30°，从而可以看出切削角度为20°时破岩效率最高，5°和30°时破岩效率最低。

2） 破岩比能随着切削深度的增加而减小，切削深度越大，破岩效率越高，而且当切削深度大于1.5 mm时，破岩效率随切削深度增加趋势大幅减缓。

图13　破岩过程能量曲线

图14　切削角度与破岩比能关系曲线

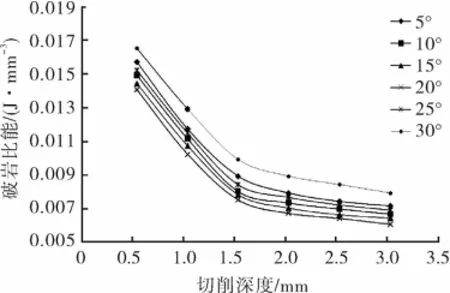
图15　切削深度与破岩比能关系曲线

4　结论

1） 建立了基于ABAQUS的锥形PDC齿切削岩石有限元分析模型，塑性阶段采用DruckerPrager准则，以等效塑性应变作为岩石的破坏准则。

2） 根据数值仿真、理论分析阐述了锥形PDC齿切向上以剪切破坏为主、侧向上以挤压拉伸断裂破坏为主的破岩机理。

3） 模拟结果表明，切削角度为20°时锥形PDC齿破岩效率最高，5°和30°时破岩效率最低；破岩效率随切削深度的增加而增加。

4） 建议继续研究建立包含围压、温度等影响因素在内的岩石弹塑性本构模型，并通过室内试验修正模型参数。

5） 建议室内试验研究不同切削角度下，锥形PDC齿的破岩效率，并与数值仿真结果进行比较分析。

［1］宋洵成，邹德永，管志川.PDC钻头等切削体积布齿优化设计［J］.石油矿场机械，2006，35（4）：61-64.

［2］鲁桂荣，肖文生，董维彬，等.PDC钻头CAD系统研究与开发［J］.石油矿场机械，2008，37（5）：22-27.

［3］杨顺辉.锥形PDC齿钻头的研制及室内试验评价［J］.石油机械，2015，43（2）：14-17.

［4］王福修.混合切削结构PDC钻头简论［J］.石油矿场机械，2005，34（3）：30-32.

［5］孙源秀，邹德永.锥形PDC齿犁切破岩受力试验研究［J］.石油机械，2014，42（9）：23-26.

［6］金国栋.全断面岩石隧道掘进机盘刀破岩机理分析（下）［J］.电站施工机械，1981（4）：21-27.

［7］虞和济，金国栋，苏禾.盘形滚刀破岩机理的有限元分析［J］.东北工学院学报，1981（3）：79-86.

［8］王春华.截齿截割作用下煤体变形破坏规律研究［D］.阜新：辽宁工程技术大学，2004.

［9］王峥荣.采煤机截齿截割过程的动力学仿真［D］.太原：太原理工大学，2009.

［10］张时忠.在截刀作用下岩石破碎机理的实验研究［J］.岩石力学与工程学报，1990，9（3）：202-208.

［11］赖海辉.岩石破碎机理的显微研究［J］.金属矿山，1981（7）：2-5.

［12］东北工学院采矿系岩石破碎研究组.牙轮钻单齿破碎岩石的初步研究［J］.东北工学院学报，1974（2）：23-45.

［13］于跃.盘刀破岩机理的细观数值模拟研究［D］.大连：大连理工大学，2010.

［14］徐小荷，余静.岩石破碎学［M］.北京：煤炭工业出版社，1984：191-192.

［15］林家骥.研究盘形滚刀破岩机理与提高刀具使用寿命［J］.福州大学学报（自然科学版），1990，18（1）：108-113.

［16］刘德顺.滚刀破岩拉槽间距研究［J］.焦作矿业学院学报，1993（3）：86-91.

Simulation Research of Conical PDC Cutter Rock-Breaking Mechanism

DOU Ninghui，YANG Shunhui
（Sinopec Research Institute of Petroleum Engineering，Beijing 100101，China）

Conical PDC cutter as a new break the rock，the theory is still in initial phase in China. By choosing DruckerPrager criterion as the rock constitutive model，equivalent plastic strain as the failure criterion，the FEA model of rockcutting by conical PDC cutter was established，which was based on ABAQUS.Through numerical simulation and theoretical analysis，the rockbreaking mechanism of conical PDC cutter was elaborated：shear failure in tangential and tensile fracture failure in lateral direction，“adjacent”effect was also elaborated.The influence laws between rockbreaking efficiency and cutting depth as well as cutting angle were simulated，and the optimal cutting angle 20°was selected.The rock breaking model of the conical PDC cutter is plowbreaking of the PDC bit.

conical PDC cutter；rockbreaking mechanism；numerical simulation；cutting angle

TE921.102

A

10.3969／j.issn.1001.3482.2015.11.003

1001-3482（2015）11-0012-06

2015-05-03

国家科技重大专项“中东富油气区复杂地层井筒关键技术”（2011ZX05031-004）

豆宁辉（1984），男，甘肃庆阳人，工程师，2010年毕业于中国石油大学（北京）油气井工程专业，主要从事钻头、深水钻井、井壁稳定等方面研究，Email：dounh.sripe＠sinopec.com。