Determination of penetration depth at high velocity impact using finite element method and artificial neural network tools

Namık KILIÇ*，Bu¨lent EKICI，Selim HARTOMACIOˇGLU

aComputer Aided Engineering Department，Otokar Otomotiv ve Savunma San.A.S，Atatu¨rk Cad No:9 Arifiye，54580，Sakarya，Turkey

bDepartment of Mechanical Engineering，Faculty of Engineering，Marmara University，34722，Istanbul，Turkey

cDepartment of Mechanical Engineering，Faculty of Mechanical Education，Marmara University，34722，Istanbul，Turkey



Determination of penetration depth at high velocity impact using finite element method and artificial neural network tools

Namık KILIÇa，*，Bu¨lent EKICIb，Selim HARTOMACIOˇGLUc

aComputer Aided Engineering Department，Otokar Otomotiv ve Savunma San.A.S，Atatu¨rk Cad No:9 Arifiye，54580，Sakarya，Turkey

bDepartment of Mechanical Engineering，Faculty of Engineering，Marmara University，34722，Istanbul，Turkey

cDepartment of Mechanical Engineering，Faculty of Mechanical Education，Marmara University，34722，Istanbul，Turkey

Determination of ballistic performance of an armor solution is a complicated task and evolved significantly with the application of finite element methods（FEM）in this research field.The traditional armor design studies performed with FEM requires sophisticated procedures and intensive computational effort，therefore simpler and accurate numerical approaches are always worthwhile to decrease armor development time. This study aims to apply a hybrid method using FEM simulation and artificial neural network（ANN）analysis to approximate ballistic limit thickness for armor steels.To achieve this objective，a predictive model based on the artificial neural networks is developed to determine ballistic resistance of high hardness armor steels against 7.62 mm armor piercing ammunition.In this methodology，the FEM simulations are used to create training cases for Multilayer Perceptron（MLP）three layer networks.In order to validate FE simulation methodology，ballistic shot tests on 20 mm thickness target were performed according to standard Stanag 4569.Afterwards，the successfully trained ANN（s）is used to predict the ballistic limit thickness of 500 HB high hardness steel armor.Results show that even with limited number of data，FEM-ANN approach can be used to predict ballistic penetration depth with adequate accuracy.

Finite element method（FEM）；Artificial neural network（ANN）；Multilayer perceptron（MLP）；Generalized feed forward（GFF）；Ballistics；High hardness armor

1.Introduction

The ballistic penetration modeling has become of prime importance in development of armor solutions and continues to be a challenging research field for engineers.Due to its complexity，in investigation of ballistic penetration problems，three modeling approaches are quite popular.These are experimentallyderivedempiricalformulation，analytical modelderivationandnumericalsimulation.Numerous empirical formulations were derived with the tests conductedin laboratory environment and used in solution of ballistic problems［1］.In contrary to straight forward methodology of deriving empiric formulation，their limited applicability to various cases is a bottleneck for widespread usage.Analytical models are quite useful due to their direct applicability on various problems but derivation always requires simplified assumptions in governing equations which results in deviation from realistic outcomes［2，3］.It is inherent that，empirical and analytic approaches cannot capture the complex nature of impact phenomenon，thus numerical simulation has become a necessary tool for the study of ballistic penetration.Numerical methods and subsequent computing technologies have been developed to the level where mentioned complex penetration behavior can be truly estimated.A review of the impact simulation literature shows that the researches under this topichave been focused on the implementing explicit hydro-codes［4-8］.

Although FE analysis is a powerful tool，due to the difficulty of development procedure and high computational cost，easy to apply approaches are always valuable for armor development studies.Especially，a computational tool which is based on limited data will decrease the number of computationally high cost numerical simulations and physical tests. The neural network approach is one of the most powerful computer analysis techniques which is based on the statistical regression.The neural network is currently used in many fields of engineering especially for modeling complex relationships which are physically difficult to explain.One of the distinguishing characteristic of neural networks is their potential to gain knowledge of problems by means of training and，after sufficient training to be able to solve problems of the same class.

Artificial Neural Networks（ANNs）have been developed over last three decades，started with the modeling of the functions of human brain by McCulloch and Pits［9］and have been used in solution of many problems in science and engineering［10-12］.In some of the studies，neural network models were not used to predict only the system behavior but also inverse form of ANNs were developed to optimize performance of complex engineering systems by finding best input parameters［13］.In the recent studies，there is a significant attempt to use ANN（s）with FE simulations especially to reduce computational time where extensive number of FE simulations required.Arndt et al.［14］was implemented a FEM-ANNapproachtoanoptimizationproblemfrom groundwater engineering.The proposed approach simply uses the FE results in training and testing of the developed ANN，and the trained ANN is used for further predictions to perform optimization loop.In that case，the process time was decreased by 60%when compared with simulation based solution. Similar approach has been used successfully by a few more researchers［15-20］.Hambli（et al.）［15，16］used FEM-ANN approach in various applications in mechanics.Gudur and Dixit［17］developed a hybrid model consist of radial basis neural networks，which was applied for the modeling of cold flat rolling process.The required training，testing and validation data have been prepared by using finite element code. ShabaniandMazahery［18］developedneuralnetwork modeling in order to predict the mechanical properties of A356.Haj-Ali et al.［19］presented a FEM-ANN modeling approach to characterize the indentation behavior of inelastic and nonlinear materials.Literature survey on FEM-ANN method shows that，it is significantly beneficial in replacing time consuming repeated FE simulations.

When ballistic penetration limit of an armor solution is required for various impact velocities and thicknesses，it is impractical to simulate all combinations to find an accurate value due to computational cost.FE simulation of such a complex ballistic problem requires high level computational sources.The integrated FEM and ANN methodology proposed in this study can predict the ballistic limit thickness for various cases.Fig.1 presents the framework of the methodology for the process of penetration depth determination.From Fig.1，it can be seen that，the preliminary study starts with a reliable FE model preparation.After reasonable correlation achieved between tests and FE simulations，data generated for ANN model.With a well trained ANN，the required number of prediction can be easily produced with a simple personal computer in minutes to find ballistic penetration limit for a given velocity.

In this paper，ballistic limit thickness of 500 HB hardness armor steel，（Secure 500）was determined against 7.62 mm 54R B32 API ammunition by using FE and neural networks. In order to eliminate memorizing behavior of ANN，the data set for training and test are intentionally chosen from 450 to 750 m/s speed range and trained model was used in prediction penetration depth at 854 m/s bullet impact velocity.The network trained with FE generated data shows significant ability to predict penetration depth，thus ballistic limit thickness was found with reasonable error.

2.Data generation with FE simulations

2.1.FE model establishment

In ballistic performance studies，it is important to use well defined threat identification both in test and simulations.For ballistic tests，numerous international standards have been developed to standardize protection levels according to ammunitions available for civilian and military applications.In this study a widespread standard，NATO Stanag 4569［21］will be used.In Stanag 4569，protection level for logistic and armored vehicles specified in five classes.The kinetic energy threat subject to this study is denoted by Level-3，in which the ammunition is named as 7.62×54 B32 API and specified impact velocity is 854 m/s with a tolerance of+/20 m/s.The 7.62 mm armor piercing bullet geometry is shown in Fig.2 which has a total mass about 10 g.The bullet consists of a hardened steel core which is inserted in a jacket.A cap of lead-antimony is placed in front of the core to stabilize the projectile during flight and penetration.A copper jacked is wrapped over the core，cup and lead antimony cap.

In numerical model，the material is discretized into finite sections over which，the conservation and constitutive equations are solved.The way in which this spatial discretization is usedleadstodifferentnumericalmethods.Themost commonly performed discretizations are Euler，Lagrange，Arbitrary Lagrange Euler（a mixture of Lagrange and Euler）and SPH（Smooth Particles Hydrodynamics）.Kilic and Ekici［22］presented a comparative study to demonstrate applicability of Lagrange and SPH techniques on determination of ballistic performance and concluded that，Lagrange method is more effective in visualizing target deformation pattern.In the Lagrange method the numerical domain moves with the material，which is ideal for following the motion and deformation in regions of relatively low distortion，and possibly large displacement.This formulation is extensively used because its advantages，such as being able to follow accurately material boundariesandintegratecomplicatedmaterialmodels.Conservation of mass is automatically satisfied in Lagrange method and material interfaces are defined precisely.The disadvantage of Lagrange is that the numerical domain can become heavily distorted in a deformation region，which can result in negative effects on the accuracy and extends the computation time.

Fig.1.Integrated FEM and ANN framework.

The geometric model consists of diameter 300 mm circular armor steel target and ammunition as shown in Fig.3.The dimensions of the plate ensure that the stress waves reflected from the edge induces no forces on the bullet during the course of the penetration.In most of the studies，projectile model consists of hardened steel core，only in a few recent researches［8，23，24］，projectile modeled including jacket，fillers and sabot.During solution domain generation，a small radius was introduced at the tip of the hardened steel for smooth mesh generation.The head of the bullet core nose was modeled with rigid elements to eliminate mesh tangling.The circular target plate is divided into three mesh regions though radial direction.The mesh topology is coarsening from inner to outer region with respect to point of contact of the bullet.The meshtransition between regions is good enough to eliminate stress wave reflections at the transition surfaces.The armor plate is meshed with hexagonal solid elements of 0.2-1 mm varying size.Exceptfront andrear lead-antimony caps，Johnson-Cook model properties are assigned to all materials.The lead-antimonycapsaremodeledwithmaterialcard ISOTROPIC-ELASTIC-FAILURE available in Ls-Dyna.This material card introduces non-iterative plasticity behavior with simple plastic strain failure model.When the effective plastic strain reaches the failure strain，the element loses its ability to carry tension.As the elements are eroded the mass remains and continues to interact with the contacting surfaces.

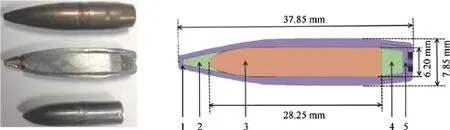
Fig.2.General view and cross-section of 7.62 mm AP ammunition.1-Brass jacket，2-Lead antimony point filler，3-Hardened steel core，4-Lead antimony base filler，5-Cup.

2.2.Material modeling

Penetration mechanism during ballistic impact is a challenging task to represent numerically.Largedeformations，high strain-rates，temperatures，localization of failure of target material needs complicated modeling of material behavior.The material behavior model should include the stress-strain relationship at large strains or different strain rates.In this constitutive model，also accumulation of damage and mode of failure should be takeninto account.Acommonlyusedmaterialmodel in ballistic penetration studies is Johnson-Cook model which also available in most of the commercial hydro-codes.The J-C model is a visco-plastic model for ductile metals.This model uses strain hardening，strain rate and thermal softening effects on material behavior and fracture［25，26］and has been successfully applied in former ballistic simulation studies.

The duration of ballistic impact is around 40 μs for the associated velocities at 850 m/s which implies that the element deformations will be large and the type of deformation will be ductile plastic damage.Johnson and Cook［25］express the equivalent stress as a function of plastic strain，strain rate and temperature with an empirical relationship for the flow stress，which is represented as

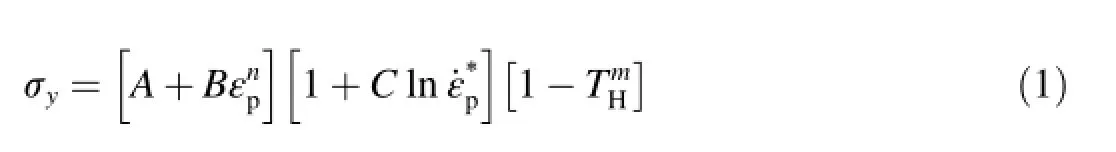
where εpis the equivalent plastic strain，is the dimensionless plastic strain rate foris normalized temperatureThe five material constants are A，B，C，n and m.The term in the first set of brackets gives the stress as a function ofand TH=0.The terms in the second and third sets of brackets represents the behavior of strain rate and thermal softening in that order.For each phenomenon，strain hardening，strain rate hardening and temperature an independent term is created.Multiplying the terms of effective plastic strain，plastic strain rate and temperature a flow stress is obtained.The constitutive model is relatively easy to adjust since it allows the separation of various effects.Due to this asset，the model is frequently used in ballistic studies.

In order to represent ductile fracture，Johnson and Cook［26］used a model combining the effects of stress triaxiality，temperature and strain rate on failure strain.The J-C damage model is a cumulative damage-fracture model.In other words，model assumes that damage collected in the material during plastic straining and the material breaks when the damage reaches a critical value.Parameters of strain hardening D1，D2and D3are mostly dependent of the stress state and for metals predominant compared with two others；strain rate hardening and thermal softening［26］.

The damage of an element is defined on a cumulative damage law by

in which Δε is the increment of the plastic strain during an integration cycle and εfis the equivalent strain to fracture under the current conditions of stress，strain rate and temperature.The damage variable D take values between 0 and 1，here D=0 for an undamaged material and failure of the elements assumed to occur when D=1［26］.

The general expression for strain at fracture is given by

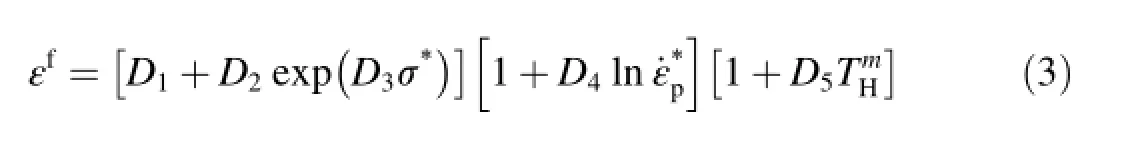
Fig.3.Numerical setup for the impact simulation.

Table 1 The mechanical properties of Secure 500 armor steel.

The dimensionless pressure/stress ratio（σ*is the ratio of hydrostatic stress per effective stress）is a measure of triaxiality of the stress state and defined as

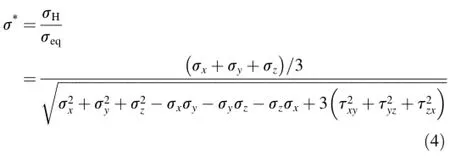
where σHis hydrostatic stress and σeqis effective or equivalent stress.The dimensionless strain rateas indicated in J-C strength model is equal towhereis reference strain rate.

The armor material used in monolithic and layered ballistic tests and simulations is a product of ThyssenKrupp Steel and known as Secure 500.As defined in material specification given by company，Secure 500 is an alloyed，liquid-quenched and tempered high-strength special steel for civil use which can be used for ballistic purposes.The mechanical properties based on manufacturer data sheet are given in Table 1.

The detailed characterization of stress strain behavior of the armor steel can be found in Kilic and Ekici［22］and the main results are summarized below.The laboratory test data are grouped in two types.The first series of tests were consisting of the quasi-static cases at large strains performed at room temperature.Quasi-static tests were performed on 10 mm thickness flat specimens at four strain rates，which are 10-4，10-3，10-2and 0.1 s-1.Specimens were machined by wire erosion cutting in transverse with respect rolling direction to represent the lowest mechanical properties.

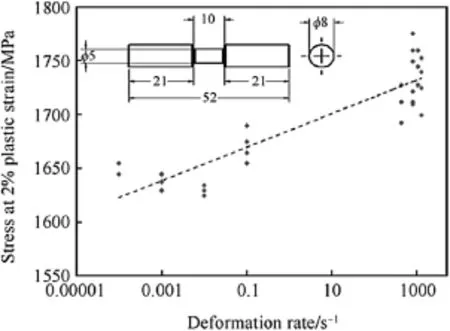
Fig.4.Stress magnitudes at 2%plastic strain for quasi-static and high strain rates.

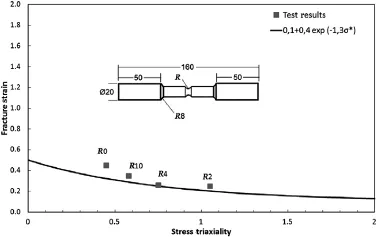
Fig.5.Triaxiality versus fracture strain data evaluated by tensile tests performed at quasi-static strain rates using notched specimens.

The yield stress parameter，A and the strain hardening parameters B and n for the J-C constitutive relation in Eq.（1）were determined from the quasi-static tensile tests.As explained before the constitutive equations require knowledge of the plastic deformation and after necking the true stressstrain values are not exact values.Therefore in model derivation the elastic part is subtracted from data.Setting A to yield strength and the data σy-A versus εpare drawn in a loglog graph then the parameters B and n were determined.In order to determine the strain rate hardening parameter C，cylindrical specimens used in Split Hopkinson pressure bar（SHPB）test setup.Zukas［1］has classified impact response by striking velocity.In 500-1000 m/s range，primarily viscous material strength is still significant and strain rates are around 103-104s-1.Preliminary ballistics simulation studies have shown that，during penetration mostly strain rates are around 1000-5000 s-1.Unfortunately，during SHPB tests strain rate around 5000 s-1cannot be reached and only strain rates 420，780，1050 and 1250 s-1could be generated on specimens to establish high strain rate dependency.In order to control strain rate，3 and 4 mm specimen diameters and 10，15 and 30 mm specimen gauge lengths were used.Stress value at 2%plastic strain is collected from quasi-static and high strain rate testsand a curve of stress versus deformation rate at logarithmic scale is drawn as shown in Fig.4，then the slope of this curve calculated to find parameter C.Thermal softening parameter“m”is taken as unity to identify linear temperature dependence without performing tests.

Fig.6.Failure parameters curve fit with tensile test results performed at various strain rates.

Fig.7.Quasi-static and high strain rate test results.

In experimental studies of Hancock and Mackenzie［27］，they concluded that the strain to failure is mostly dependent on the stress state，therefore parameters D1，D2and D3are dominant when compared to others.Many authors used the equation developed by Bridgman［28］that describes the connection between necking radius and flow stress on a notched specimen.In this study similar approach given by Teng and Wierzbicki［29］was used.Failure parameters determinedbytensiletestsperformedinquasi-static isothermal conditions.To find different stress triaxiality at failure，specimens with the same cross section diameter but different notch radius were used.The first is unnotched，the second have a 2 mm，third have 4，and fourth have 10 mm notch radius respectively.After the triaxial states of stress are obtained for each specimen，then constants D1，D2and D3defined in Eq.（3）are estimated by curve fitting as shown in Fig.5.Since strain rate parameter can be taken into account in the separate bracket，there is no need to perform a high strain rate test with notched specimen.Additionally，tests should include the high strain rate condition that is similar with the simulations.Therefore fracture strains are collected from cylindrical specimens used in SHPB tests and included in Fig.6 to found strain rate dependency and D4was estimated by calculating the slope of linear curve fit.As in the previous cases，SHPB test were carried out at room temperature.

Fig.8.J-C constitutive parameters curve fit to calculate strain rate coefficient.

The armor piercing bullet used in this study has a hardened steel core whose hardness is around 830-880 HV.The hardened steel core gives the significant penetration capability to the bullet therefore a detailed study on material characterization will increase the consistency of the simulations.As in target material case，material test program for bullet was performed by IYTE dynamic test laboratory but due to logistic reasons both dimensions and quantity of test specimens vary greatly with respect to armor case.In this study miniature specimens were prepared from cylindrical part of steel core after cutting the ogive nose.The cylindrical parts machined to have a smooth notched cross section to prevent early failures during tensile tests without going into plastic deformation.The test program includes both quasi-static tensile tests and SHPB dynamic tests performed in room temperature conditions.As expected due to high hardness values and brittle behavior of specimens，most of the failures occurred without plastic deformations.On only a few specimens，reasonable test results could be evaluated to develop J-C parameters.No doubt the number of tests will not have a high confidence from statistical point of view but will be beneficial to understand the at least the main characteristics of steel core.

Similar approach defined in armor modeling is used.The yield stress parameter，A and the strain hardening parameters B and n for the J-C constitutive relation in Eq.（1）were determined from the quasi-static tensile tests.Fig.7（a）shows the measured quasi-static true stress versus true strain curves for armor material until the fracture.In model derivation the elastic part of quasi static tensile tests are subtracted and only values before necking was used.Setting A to yield strength and the data σy-A versus εpare drawn in a log-log graphthen the parameters B and n were determined.In order to determine the strain rate hardening parameter C，cylindrical specimens used in split Hopkinson pressure bar（SHPB）test setup.The tensile test results for high strain rate case are plotted in Fig.7（b）.As shown in Fig.8 stress values at a specific strain were plotted for three strain rates and J-C constitutive parameters were derived using curve fit.Temperature dependence is assumed to be linear and thermal softening parameter“m”is taken as“1.0”.Failure parameter evaluation was absent due to lack of appropriate specimens. The materials model parameters of the target，bullet and jacket used in the simulations are tabulated in Table 2.

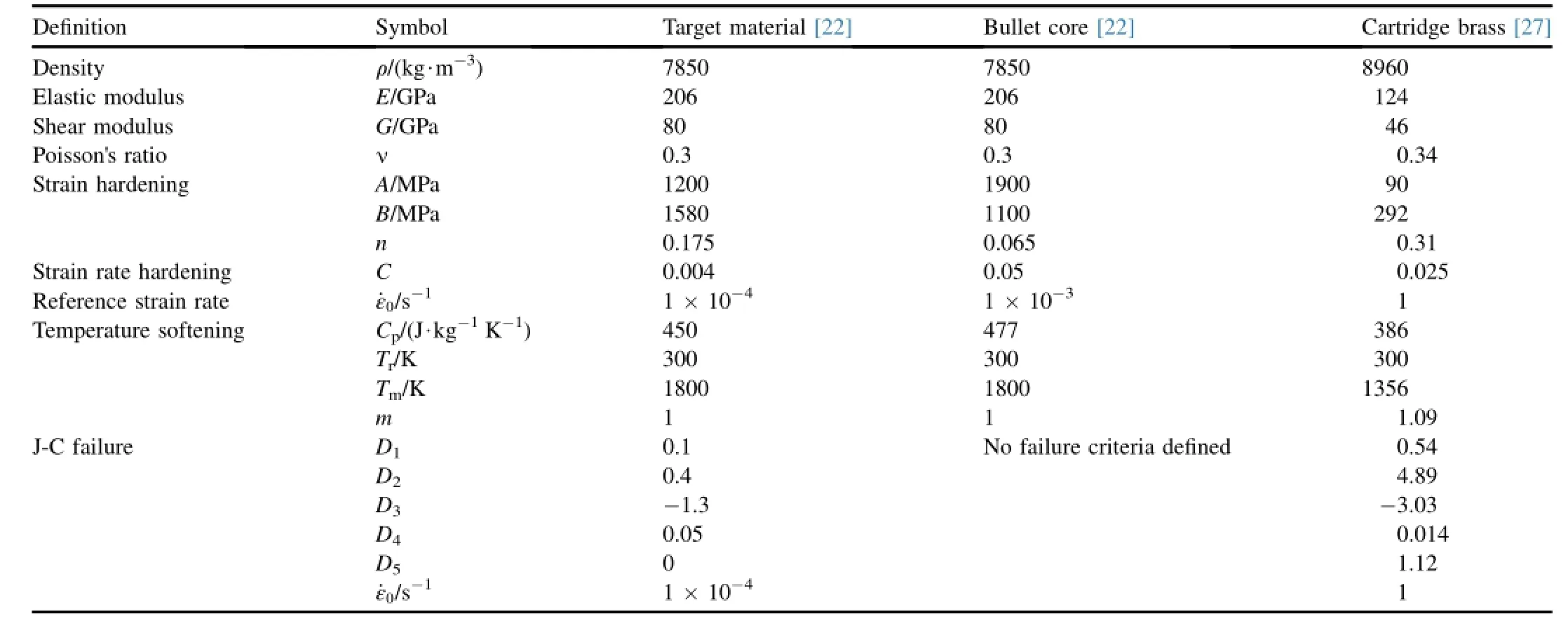
Table 2 Material parameters used in simulations.

2.3.FE simulation validation with ballistic tests

Numerical simulations for 20 mm thickness target have been performed to investigate whether the computational model is able to predict the experimentally found target response，such as penetration depth or crater formation.The penetration results are plotted in Fig.9.In the first phase the jacket indents the target plate and lead-antimony cap is quickly eroded.The damage on the target increases in the contact region due to plastic straining of the elements close to projectile.As the cumulative damage reaches a threshold value，elements are eroded which means no strength remains after deletion of an element.

Fig.9.Deformation plots for 20 mm target at various time steps.

In test the depth of crater was found between 12.3 mm and 12.9 mm and the approximate diameter of crater was around 13.1-15.5 mm.The conformity on penetration depth is quite good for the experimental and numerical results.Although the spall and cavity formation behavior is successively simulated as shown in Fig.10，prediction requires further improvement on crater diameter which is underestimated by 20%.The back face deformation found in experiments is also simulated successfully.As a conclusion，the numerical model seems to represent the perforation behavior can be used in data generation for ANN model.

3.Neural network model development

MLP is very popular and used more than other neural network types for modeling complex relationships between input and output variables.Although MLP is extensively used in all engineering fields，the number of studies performed on ballistics is rare.Fernandez-Fdz and Zarea［30］developed a two levels MLP model to establish a toll for lightweight ceramic-aluminum armor design.Their model was based on hyperbolic tangent and logistic activation functions and 200 impact cases were created with FE simulations for learning，cross validation and testing.Their study shows that MLP can predict residual velocity with an accuracy of%7.5.A similar study was performed by Renahan et al.［31］to find ballistic penetration depth of ceramic target using MLP.The data used in the ANN model were collected from experimental shot trials on ceramics plates.Over 300 data vectors used to develop the ANN to predict penetration depth.They found that，for lower target thicknesses，the predicted and real values have a good correlation but when the higher plate thicknesses were considered，the error calculated between predictions and tested goes up to 15%.Garcia-Crespo et al.［32］has developeda MLP back propagation network to predict the ballistic behavior of steel armor against high speed impact.The data was collected using FE simulations to train and validate neural network.The network developed has a mean error less than 7%.This study shows that MLP is a promising tool for ballistic performance studies although the chosen network has one of the simplest architecture available in literature. Gonzalez-Carrasco et al.［33，34］has presented comprehensive studies to find optimized parameters of neural network for ballistic impact problems.They compared various neural network types，training algorithms，error cost function selections and data selection methods for training.Their results demonstrate that a well trained MLP can be used successively in determination of ballistic limit velocity and mainly this study is motivated by their outcomes.

Fig.10.Comparison of penetration depth found in test and simulation.

For the ANN model，a three level MLP architecture was chosen as shown in Fig.11.The hidden layers，basically，provide the networks ability to generalize performance of outputs.In theory，a continuous function can be approximated by one hidden layer with enough hidden units.In most cases，one or sometimes two hidden layers are used.In this study one hidden layer is chosen.The adequate number of hidden units depends on many factors.Some of them are number of training patterns，number of input and output units，type of activation function，training algorithm.When too few hidden units used，generally results in high training error due to under fitting.When too many used，obviously results in low training errors，but will make training unnecessarily slow.In other words，there is not a general procedure for selecting the optimum number for hidden units.The reasonable strategy is to try a series of hidden units and find a number which works best.In this study，the maximum number of hidden unit is chosen to be forty and decreased to investigate affect on accuracy.

Fig.11.The multilayer perceptron structure used in simulation.

In order to show that，developed network models can learn complex relationship between input and output parameters，intentionally the number of inputs has been chosen to be as few as possible.For a specific threat and type of armor，the most affecting parameters on ballistic performance and penetration are bullet incident velocity and thickness of the armor.Therefore the number of inputs for neural model is chosen to be two.In literature there is not a specific rule to determine amount of training data set.Fernandez-Fdz and Zarea［30］have randomly chosen training data set to be 85%. Renahan et al.［31］has also chosen training data randomly and amount is approximately 80%of data set.Gonzalez-Carrasco et al.［35］has divided input data randomly to be 80%training and 20%for testing.In this study，the high speed and high hardness cases are eliminated from training data set and used for testing and validation to demonstrate that neural networks trained with low-medium incident velocity range，can predict accurate results for higher velocities.

Since the main objective of this study is to decrease computation time，using small number of data during training without scarifying the accuracy of predictions has a significant importance.Gonzales-Carrasca et al.［35］has achieved 6% error with forty FE simulations which is the least one authors are aware of.In this study only twenty impact simulations are performed and tabulated in Table 3.In order to yield numerical stability，normalization has been applied to transform input and output variables into homogeneous and well-behaved values.The below formulation was used to normalize values between 0.1 and 0.9 for sigmoid function and between-0.9-0.9 for hyperbolic tangent function

Activation functions for the hidden units are required to introduce non-linear weight adjustment to improve networkprediction capability.The most common activation function is sigmoid（logistic），which is typically used for mapping continuousdatasetsandgivenbyequation f（x）=（1+exp（-x））-1.The choice of activation functions for each layer is commonly based on experience of researchers.For example Gonzales-Carrasco et al.［35］has chosen hyperbolic tangent activation function based on literature survey suggests sigmoid activation.A general rule indicates that；for problems which involve learning about an average behavior sigmoid function can be used and if the problem involves learning about deviation from an average，hyperbolic tangent function was proposed.The hyperbolic tangentfunctionisgivenbyequationf（x）=（exp（x）-exp（-x））/（exp（x）+exp（-x））.In this study，both sigmoid and hyperbolic tangent functions are investigated.

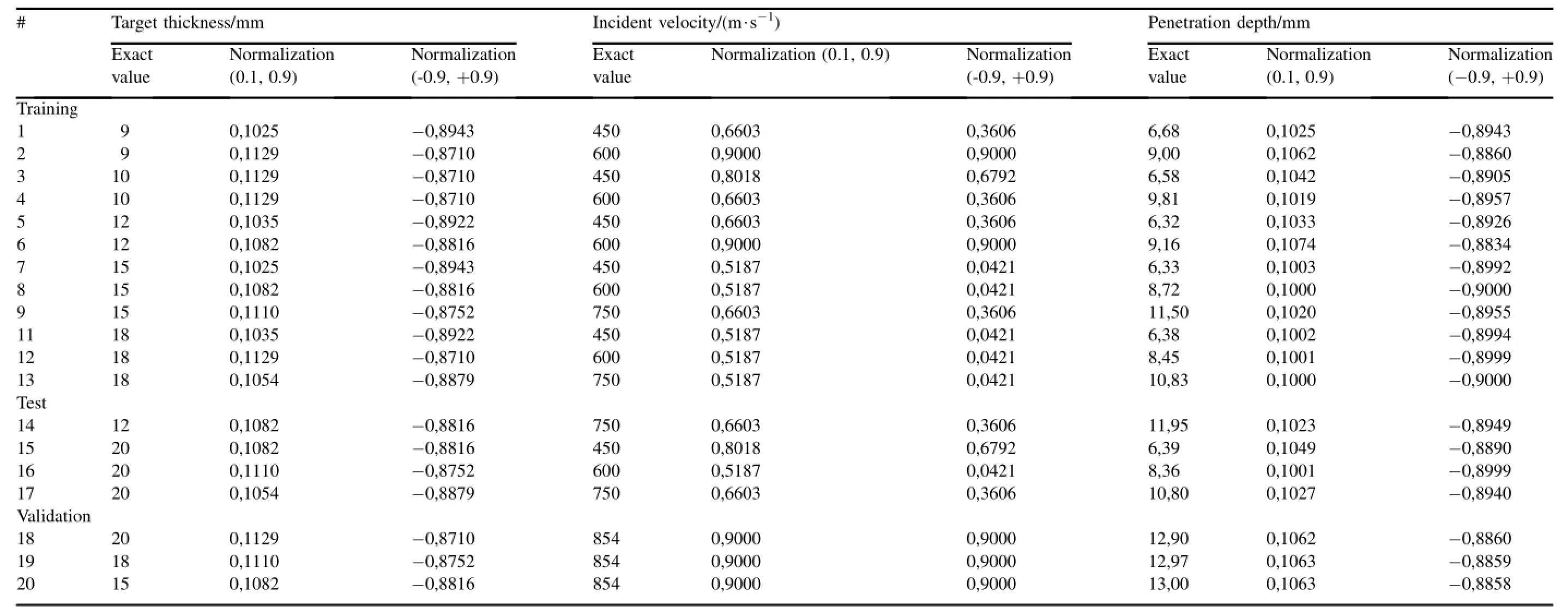
Table 3 Normalized data for ANN training，test and validation.

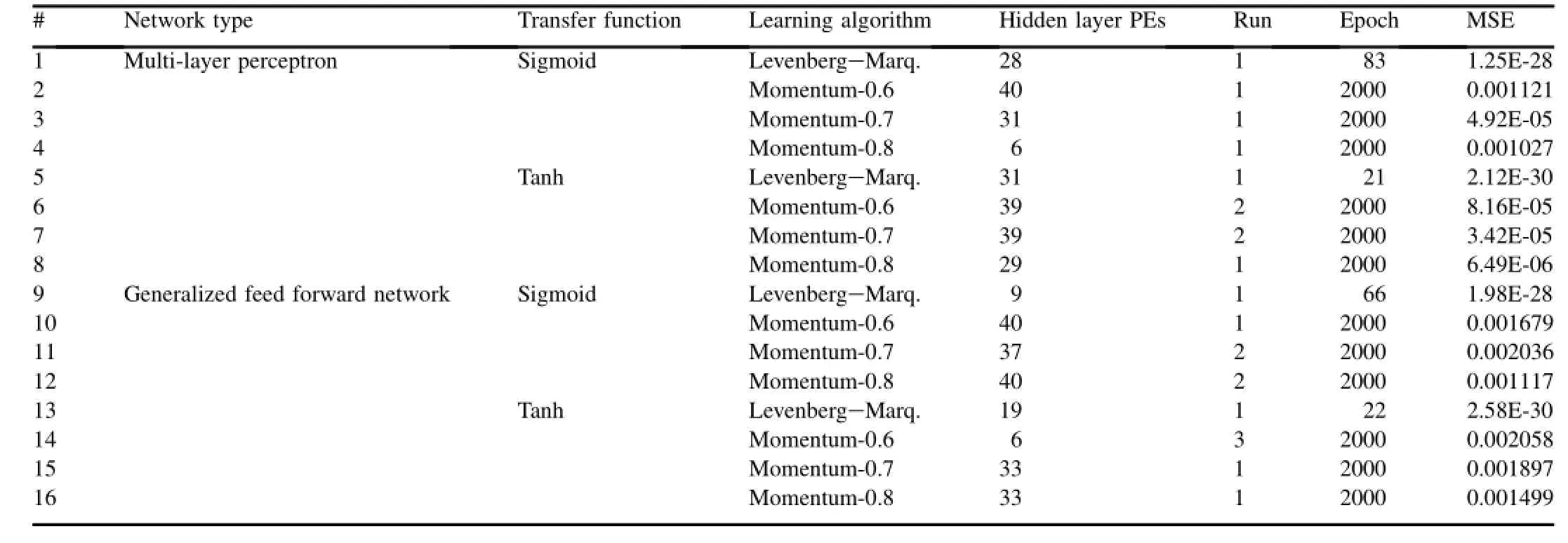
Table 4 Network architect optimization studies.

One of the significant features of the neural networks is the back propagation algorithm which is known as gradient decent and its convergence and speed is controlled by learning rate and momentum coefficients.It is the most popular and easy to learn algorithm for complex multilayer networks.Although its widespread usage，due to its slow convergence，Gaus-Newton algorithm was developed to increase the speed but this time，stability advantage of gradient decent was lost.As an alternative to eliminate bottlenecks of back propagation and Gaus-Newton algorithms，the Levenberg-Marquardt algorithm proposed to find solution to slow convergence.This algorithm is suitable for small-medium sized problems.The basic idea of the Levenberg-Marquardt algorithm is that，it performs a combination of gradient descent for stability and Gauss-Newton algorithm for the speed of convergence［36］.

3.1.Training of ANN（s）

For the network design，three layer MLP and GFF architectures were selected.Sigmoid and hyperbolic activation functions for hidden and output layers were used.As learning algorithm，Levenberg-Marquardt and back propagation with momentum coefficients 0.6，0.7 and 0.8 were used.A network learns most effectively if all neurons are learning roughly at same speed.In this study，although learning rate in back propagation will highly influence the convergence speed，the default values proposed by code Neuro Solutions V5 were used.As shown at Table 4，totally 16 different network topologies were developed and for the each topology，by changing number of hidden points and number of training runs，the minimum value of the mean squared error（MSE）was calculated.A preliminary study on epoch number for a set of hidden points has shown that，MSE curve is reached its minimum around epoch number 2000 and is almost linear above this value.Therefore in the training the maximum epoch number was chosen to be 2000.For the developed sixteen network topologies，number of hidden layer points varied between 1 and 40 and training runs between 1 and 3，totally 1920 training trials were performed to find minimum values achieved for minimum MSE.Table 4 shows number of hidden points，epoch number and number of training pass achieved for the min MSE values.Based on training results，the minimum MSE has achieved by topology#5，which is MLP with hyperbolic activation function，Levenberg-Marquardt learning algorithm and includes 31 hidden points.The maximum MSE has found on topology#14 which is GFF with hyperbolictangent activation function，back propagation algorithm with momentum value 0.6，3 times training with 6 hidden points. The advantage of using Levenberg-Marquardt algorithm on convergence is easily shown by comparing epoch numbers. With respect to back propagation，with Levenberg-Marquardt learning algorithm around 30-90 times faster convergence was achieved.In most cases regardless of the used learning algorithm，using hyperbolic tangent activation has resulted lower MSE values.In general MLP based networks and GFF ones shows similar error values.

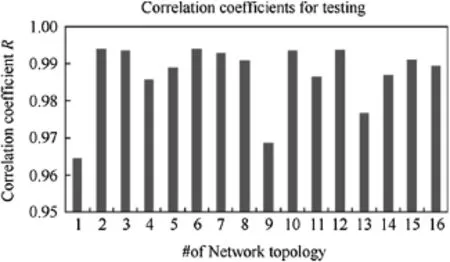
Fig.12.Correlation coefficients calculated for each network topology.

3.2.Testing of ANN（s）

After best number of hidden points and number of run determined，each network topologies were tested with the data given in Table 3.Correlation coefficients were calculated during testing and presented for each network in Fig.12. Correlation coefficients are over 0.95 for all network topologies means that precise results can be achieved between input variables and penetration depth.A significant reason of high correlation coefficients found is definitely due to normalization applied.In studies where the data set was generated with the shot tests in laboratory environment，the correlation coefficients may not be as high as found in this study due to noise affects.The high correlation values also show the adequacy of FE simulation methodology used.

Fig.13.Percentage error calculated during ANN testing.

The percentage error calculated for each network topology during test and validation and represented in Fig.13.Network topologies 1，3，5，6，7，8，9，14 have the minimum MSE values after training，shows percentage error over 5%according to test and validation.The networks which have percentage error over 5%were eliminated（topologies 1，3 5，6，7，8，9，13，14，15，16）and only networks having error percentage below 5% were taken into account（topologies 2，4，10，11，12）for further studies.The networks represented by#2 and#12 have the minimum error and maximum correlation coefficients.The network topology denoted by#2 is a MLP with sigmoid transfer function and back propagation learning algorithm with momentum coefficient of 0.6.The mentioned network has forty hidden layer neurons，epoch number achieved is 2000 and number of training run is 2.The network has achieved 1.12× 10-3MSE value during training，in testing 2.19% percentage error was found and correlation coefficient was 0.994.The percentage error was decreased to 1.48%in validation phase.The network topology denoted by#12 is a GFF with sigmoid transfer function and back propagation learning algorithm with momentum coefficient of 0.8.The mentioned network has thirtyseven hidden layer neurons，epoch number achieved is 2000 and number of training run is 2.The network has achieved 1.12× 10-3MSE value during training，in testing 2.19%percentage error was found and correlation coefficient was 0.994.In validation percentage error was decreased to 1.04%.

In general，testing and validation results show significant variation in error values when compared with training results. Although in training with Levenberg-Marquardt learning algorithm relatively low error values could be achieved，in test and validation back propagation with higher momentum coefficients shows better results.Also it is interesting to see that the activation functions show varying affects on results.During training，hyperbolic tangent activation has decreased error values but in test and validation，sigmoid function shows better results.The error percentage difference between test and validation results is significantly low in topologies#2 and#12，which also identifies the stability of these networks.

4.Results and discussions

The testing results for 15 mm target thickness at 600 and 750 m/s impact velocities，target thickness 18 mm at 450 m/s and target thickness 12 mm at 600 m/s are graphically represented in Fig.14.It is evident that，the networks chosen are capable to predict penetration depth with high accuracy.As mentioned formerly，the data set for training and testing was intentionally chosen to have impact speeds lower than 750 m/s and the validation data set is chosen to have impact speed of 854 m/s.By the way，it can be concluded that，the developed networks can be used for prediction.

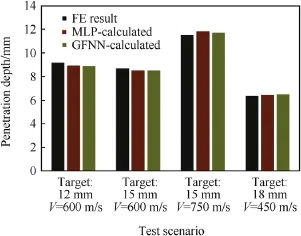
Fig.14.Testing results for best GFF and MLP topology with respect to original data.

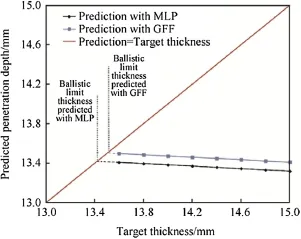
Fig.15.Penetration depth predicted for 854 m/s impact speed and target thickness between 13 and 14 mm.

Once a network is tested and validated，it can be used to simulate the penetration depth of steel armor against Stanag 4569 level 3 threats.For this purpose penetration depth calculated with ANN for the target thicknesses between 13 and 14 mm at 854 m/s impact speed，and results presented in Fig.15.The point where target thickness is equals to penetration depth is defined as ballistic thickness.In other words，the points where the line Penetration=Target thickness crossing the prediction lines are the ballistic penetration depth for the given impact velocity.The ballistic thickness found by developed networks is 13.4 and 13.5 mm with MLP and GFF respectively.Kilic and Ekici［22］have found ballistic limit thickness for this steel as 14.2 mm which is only 5%higher than the artificial neural networks predicts.A single FE simulation run on 36 CPU compute cluster with Xeon X5690 3.46 GHz processors takes 117 min.Which means the data generation required to draw Fig.15 with FE simulations takes around 20 h computation time even with highly complicated server.But with the developed ANN model，it takes only 10 min to generate same data set with an ordinary personal computer.

5.Conclusions

This study shows the effective use of FEM-ANN approach in determination of ballistic limit thickness of high hardness steels against 7.62 mm armor piercing bullet.The developed consistent FE model can be used to simulate complex nature of ballistic penetration.From the testing of the various neural network topologies and results given and discussed，the following main outcomes can be drawn:

1）Even with the limited data created for training，the proposed MLP and GFF networks assisted with FEM can predict the penetration depth for a wide range of impact velocities with accuracy and less computational time.

2）With enough number of hidden points，without necessity of a large data set，reasonable results can be achieved.

3）Training results itself not sufficient to give the decision on neural network topology.

4）The confidence of the data generated with FE simulations has a benefit to eliminate uncertainty and noise factors that a test based data may have.Therefore FEM based data generation should be taken into consideration for the effective use of ANN approach.

5）In the velocity range of 500-1000 m/s，mainly viscous material strength is dominant.Without changing the material behavior mechanism，ANN approach can be used to determine ballistic performance of armor solutions at high impact speeds with performing only low speed，low thickness scenarios.

Although its superior performance in many engineering problems，it should be noted that ANNs have also some limitations.First they are not able to explain the physical relationship between input and output variables.Therefore as commented above if the main mechanism of the system behavior changes with altering input parameters，the model predictions may not be accurate.For that reason，the developed ANN model works well for only 500-1000 m/s velocity range.Secondly，there isn't a general guideline to set architecture for a given problem.The developed network architecture is valid only for the specified ballistic problem. Another limitation of this study is，only two input parameters；threat velocity and target thickness were used in ANN model development.Increasing number of input variables may improve the prediction performance.

Acknowledgment

The authors would like to thank Otokar Otomotiv ve Savunma Sanayi A.S.for the financial support.

［1］Zukas JA，Nicholas T，Swift HF，Greszczuk LB，Curan DR.Impact dynamics.New York:J Wiley；1982.

［2］Ben-Dor G，Dubinsky A，Elperin T.Ballistic impact:recent advances in analytical modeling of plate penetration dynamics.ASME Appl Mech Rev 2005；58:355-71.

［3］Krishna Teja Palleti HN，Grusamy S，Kumar Santosh，Soni R，John B，Vaidya R.Ballistic impact performance of metallic targets.Mater Des 2012；39:253-63.

［4］Buchar J，Voldrich J，Rolc S，Lisy J.Ballistic performance of dual hardness armor.In:Proceedings of 20th International Symposium on Ballistics，Orlando；2002.p.23-7.

［5］Dey S，Borvik T，Hopperstad OS，Langseth M.On the influence of fracture criterion in projectile impact of steel plates.Comp Mater Sci 2006；38:176-91.

［6］Khoda-rahmi H，Fallahi A，Liaghat GH.Incremental deformation and perforation analysis of deformable projectile into semi-infinite target.Int J Solids Struct 2006；43:569-82.

［7］Borvik T，Dey S，Clausen AH.Perforation resistance of five different high-strength steel plates subjected to small arms projectiles.Int J Impact Eng 2009；36:948-64.

［8］Borvik T，Olovsson L，Dey S，Langseth M.Normal and oblique impact of small arms bullet on AA6082-T4 aluminum protective plates.Int J Impact Eng 2011；38:577-89.

［9］McCulloch W，Pitts WH.A logical calculus of the ideas immanent in nervous activity.B Math Biophys 1943；5:115-33.

［10］Li HY，Wei DD，Li YH，Wang ZF.Application of artificial neural network and constitutive equations to describe the hot compressive behavior of 28CrMnMoV steel.Mater Des 2012；35:557-62.

［11］Madic M，Rodavonovic M.Modeling and analysis of correlations between cutting parameters and cutting force components in turning AISI 1043 steel using ANN.J Braz Soc Mech Sci 2013；35:111-21.

［12］Haghdadi N，Zarei-Hanzaki A，Khalesian AR，Abedi HR.Artifical neural network modeling to predict the hot deformation behavior of an A356 aluminyum alloy.Mater Des 2013；49:386-91.

［13］Hattab N，Motelica-Heino M.Application of an inverse neural network model for the identification of optimal amendment to reduce Copper toxicity in phytoremediated contaminated soils.J Geochem Explor 2014；136:14-23.

［14］Arndt O，Barth T，Freisleben B，Grauer M.Approximating a finite element model by neural network prediction for facility optimization in groundwater engineering.Eur J Oper Res 2005；166:769-81.

［15］Hambli R，Chamekh A，Salah HBH.Real-time deformation of structure using finite element and neural networks in virtually reality applications. Finite Elem Anal Des 2006；42:985-91.

［16］Hambli R.Numerical procedure for multiscale bone adaptation prediction based on neural networks and finite element simulation.Finite Elem Anal Des 2011；47:835-42.

［17］Gudur PP，Dixit US.A neural network-assisted finite element analysis of cold flat rolling.Eng Appl Artif Intel 2008；21:43-52.

［18］Shabani MO，Mazahery A.The ANN application in FEM modeling of mechanicalpropertiesofAl-Sialloy.ApplMathModel 2011；35:5007-13.

［19］Haj-Ali R，Kim HK，Koh SW，Saxena A，Tummala R.Nonlinear constitutive models from nano indentation tests using artificial neural networks.Int J Plast 2008；24:371-96.

［20］Chan WL，Fu MW，Lu J.An integrated FEM and ANN methodology for metal-formed product design.Eng Appl Artif Intel 2008；21:1170-81.

［21］NATO STANAG 4569.Protection levels for occupants of logistic and light armoured vehicles.2004.

［22］Kilic N，Ekici B.Ballistic resistance of high hardness armor steels against 7.62 mm armor piercing ammunition.Mater Des 2013；44:35-48.

［23］Flores-Johnson EA，Saleh M，Edwards L.Ballistic performance of multilayered ceramics plates impacted by a 7.62-mm APM2 projectile.Int J Impact Eng 2011；38:1022-32.

［24］Iqbal MA，Gupta G，Gupta NK.3D numerical simulation of ductile targets subjected to oblique impact by sharp nodes projectiles.Int J Solids Struct 2010；47:224-37.

［25］Johnson GR，Cook WH.A constitutive model and data for metals subjected to large strains，high strain rates and high temperatures.In:Proceedings of the 7Th International Symposium on Ballistics Hauge；1983. p.541-7.

［26］Johnson GR，Cook WH.Fracture characteristics of three metals subjected to various strains，strain rates，temperatures and pressures.Eng Fract Mech 1985；21:34-48.

［27］Hancock JW，Mackenzie AC.On the mechanisms of ductile failure in high strength steels subjected to multi-axial stress-states.J Mech Phys Solids 1976；24:147-69.

［28］Bridgman PW.Studies in large plastic flow and fracture.Newyork: McGraw-Hill；1952.

［29］Teng X，Wierzbicki T.Evaluation of six fracture models in high velocity perforation.Eng Fract Mech 2006；73:1653-78.

［30］Fernandez D，Zaera R.A new tool based on artificial neural networks for the design of lightweight ceramic-metal armour against high-velocity impact of solids.Int J Solids Struct 2008；45:6369-83.

［31］Renahan CC，Andrews WS，Jaansalu KM.Modeling the depth of penetration of ceramic targets using artificial neural networks.In:Proceedings of 23rd International Symposium on Ballistics Tarragona；2007. p.1487-94.

［32］Garcia-Crespo A，Ruiz-Mezcua B，Fernadez-Fdz D，Zaera R.Prediction of the response under impact of steel armors using multilayer perceptron. Nueral Comput Applic 2007；16:147-54.

［33］Gonzalez-CarrascoI，Garcia-CrespoA，Ruiz-MezcuaB，Lopez-Cunadrado JL.Neural network application for high speed impacts classification.In:Proceeding of the World Congress on Engineering London；2008.

［34］Gonzalez-CarrascoI，Garcia-CrespoA，Ruiz-MezcuaB，Lopez-Cuadrado JL.Dealing with limited data in ballistic impact scenarios:an empirical comparison of different neural network approaches.Appl Intel 2011；35:89-109.

［35］Gonzalez-CarrascoI，Garcia-CrespoA，Ruiz-MezcuaB，Lopez-Cuadrado JL.A neural network-based methodology for recreation of highspeedimpactsonmetalarmours.NeuralComputApplic 2012；21:91-107.

［36］Rafiq MY，Bugmann G，Easterbrook DJ.Neural network design for engineering applications.Comput Struct 2001；79:1541-52.

17 October 2014；revised 5 December 2014；accepted 8 December 2014

Available online 12 January 2015

.Tel.:+90 264 229 22 44x3900；fax:+90 264 229 22 42.

E-mail address:nkilic@otokar.com（N.KILIÇ）.

Peer review under responsibility of China Ordnance Society.

http://dx.doi.org/10.1016/j.dt.2014.12.001

2214-9147/Copyright©2015，China Ordnance Society.Production and hosting by Elsevier B.V.All rights reserved.

Copyright©2015，China Ordnance Society.Production and hosting by Elsevier B.V.All rights reserved.