多限相邻排列问题初步探索
詹高娃
(华南师范大学数学科学学院,广东广州510631)
多限相邻排列问题初步探索
詹高娃
(华南师范大学数学科学学院,广东广州510631)
本文研究限定相邻元素的排列问题,由单组的限邻问题推广多组限邻问题,并得到集合中若干个不相交子集之间的限邻排列问题的解决办法,其中多次用到容斥原理、集合的交并运算和归纳与猜想原理,并对定理进行了初步的推广与应用.
限邻排列;线性排列;圆排列
0 引言
比如我们日常生活中经常遇到的排座位问题,某几个同学一定要相邻而坐或某几个同学一定不能相邻而坐;夫妻做圆桌吃饭时需要夫妻相邻或分开坐等等.这些问题在涉及排列问题中经常遇到,但是解决这些问题的通法尚未有人总结.这是本文所要解决的主要问题.
定义1对多组元素分别进行限邻控制然后排列在同一行(圈)的排列方式称为多限邻排列,即把要排列的n个元素组成的集合分为k个不相交的子集,其中每一个子集的元素要相邻(或不相邻)排列的排列方式.多限邻排列可分为多限相邻排列和多限不相邻排列两种情况.
例如,集合A={a1,a2,a3,a4,a5},其中a1,a2,a3必须相邻排列的排列,我们可以把集合A分为三个相交的集合{a1,a2,a3},{a4}和{a5},其中集合{a1,a2,a3}中元素全排列的方法数有3!种,{a4}中元素全排列的方法数有1!,{a5}中元素的全排列方法数为1!,所以集合A中{a1,a2,a3}相邻排列的方法数为3!1!1!.

引理3 n个相异元素的圆全排列方法数为(n-1)!.
1 限邻线性排列
1.1 限相邻线性排列
设A={a1,a2,…,an}是一个n元集,易得集合A中a1,a2相邻排列的排列方法数为2!(n-1)!,集合A中a1,a2,a3相邻排列的排列方法数为3!(n-2)!;由归纳证明可知:集合A中a1,a2,…,ak(1≤k≤n)相邻排列的排列方法数为L(n,k)=k!(n-k+1)!.
定理1设A={a1,a2,…,an}是一个n元集,其中,且,则集合A中的元素相邻排列的方法数为.
证明:分析可知,本题可采用“捆绑法”解决,分三步走:第一步,对Ai(i=1,2,…,k)作全排列,其排列方法数为ri!(i=1,2,…,k);第二步,对A1,A2,…,Ak这k个集合作全排列,其排列方法数为k!;第三步,利用乘法原则可知,集合A的排列方法数为.
推论1设A={a1,a2,…,an}是一个n元集,其中,且,则集合A中的元素相邻排列的方法数为

例1设A,B,…,J这十位同学一起照相,要求A,B,C,D这四位同学相邻站在一起,而且E,F,G这三位同学也要相邻站在一起,请问:总共有多少种排列方法数?
分析:此题可参照定理1,把A,B,C,D这四位同学看成是一组,E,F,G这三位同学看成一组,再把剩下的三位同学分别看成三组,此题可理解为求五组元素相邻排列的方法数.
1.2 限不相邻线性排列
设A={a1,a2,…,an}是一个n元集,易得集合A中a1,a2不相邻排列的排列方法数为;集合A中a1,a2,a3两两不相邻排列的排列方法数为;由归纳证明可知:集合A中a1,a2,…,ak(1≤k≤n)两两不相邻排列的排列方法数为.
定理2设A={a1,a2,…,an}是一个n元集,其中,,

证明:用S表示A的全排列之集,以Si(i=1,2,…,k)表示A中Ai(i=1,2,…,k)的元素全相邻排列的全排列之集,依题意需要求.

推论2设A={a1,a2,…,an}是一个n元集,其中,且i,j∈1,2,…,k),,则集合A中Ai(i=1,2,…,k)元素不全相邻排列的方法数为

例2设A,B,…,F这六位同学一起照相,要求A,B,C这三位同学不能全部相邻站在一起,D,E,F这三位同学也不能全部相邻站在一起,请问:总共有多少种排列方法数?
规定:没有指明排列方式的排列默认为线性排列.
2 限邻圆排列
2.1 限相邻圆排列
设A={a1,a2,…,an}是一个n元集,易得集合A中a1,a2相邻排列的圆排列方法数为2!(n-2)!;集合A中a1,a2,a3相邻排列的圆排列方法数为3!(n-3)!;由归纳证明知,集合A中a1,a2,…,ak(1≤k≤n)相邻排列的圆排列方法数为R(n,k)=k!(n-k)!.
定理3设A={a1,a2,…,an}是一个n元集,其中,且i,j∈1,2,…,k),,则集合A中Ai(i=1,2,…,k)的元素相邻排列的圆排列方法数为
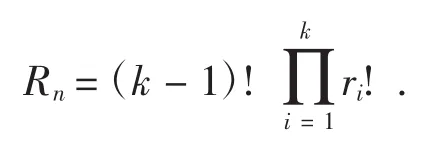
其证法与定理1类似.
推论3设A={a1,a2,…,an}是一个n元集,其中,且i,j∈1,2,…,k),,那么集合A中Ai(i=1,2,…,k)的元素相邻排列的圆排列方法数为

例3设A,B,…,J这十位同学坐圆桌吃饭,要求A,B,C,D这四位同学相邻坐在一起,而且E,F,G这三位同学也要相邻坐在一起,请问:总共有多少种排列方法数?
2.2 限不相邻圆排列
设A={a1,a2,…,an}是一个n元集,易得集合A中a1,a2不相邻排列的圆排列方法数为;集合A中a1,a2,a3两两不相邻的排列圆排列方法数为;由归纳证明知,集合A中a1,a2,…,ak(1≤k≤n)两两不相邻排列的圆排列方法数为
定理4设A={a1,a2,…,an}是一个n元集,其中,且i,j∈1,2,…,k),,则集合A中Ai(i=1,2,…,k)的元素不全相邻排列的圆排列方法数为

其证法与定理2类似.
推论4设A={a1,a2,…,an}是一个n元集,其中,且i,j∈1,2,…,k),,则集合A中Ai(i=1,2,…,k)的元素不全相邻排列的圆排列方法数为

例4设三对夫妻坐圆桌吃饭,要求夫妻双方不能坐在相邻的位置,请问:总共有多少种排座位的方法数?
总结:本文只是考虑了相异元限邻排列计数问题,该课题可由相异元推广到可重复排列计数问题,也就是让集合中元素可重复排列.
[1]曹汝成.组合数学[M].第二版.广州:华南理工大学出版社,2012.
[2]潘承洞,潘承彪.初等数论[M].第三版.北京:北京大学出版社,2013.M ulti-Set of Lim it Adjacent Prelim inary Exploration
ZHAN Gaowa
(South China Normal University,Guangzhou,510631 Guangdong,China)
In this paper,the permutation problem of limit adjacent elements is studied. The single set of limit problem is extended to multi-set of limit problem by using inclusion-exclusion principle,collection of occurring simultaneously and principle of induction and conjecture frequently.A solution to deal with limit adjacent arrangement problems about collection of several disjoint subsets is achieved.Preliminary popularization and application of the theorem are also studied.
limit neighborhood adjacent;linear adjacent;round adjacent
O 157
A
1001-4217(2015)02-0034-05
2014-09-30
詹高娃(1992-),女,广东饶平人,研究生竞赛数学方向在读.E-mail:2841254805@qq.com

