一类哑铃图的优美性和奇强协调性

童细心

（广东省汕头职业技术学院自然科学系，广东汕头515041）

一类哑铃图的优美性和奇强协调性

童细心

（广东省汕头职业技术学院自然科学系，广东汕头515041）

研究了哑铃图2Cn+{unv1}的优美性和奇强协调性，得到了哑铃图2Cn+{unv1}在n=4k时是优美图和奇强协调图等结论.

哑铃图；优美图；奇强协调图

0 引言

图论是数学的一个重要分支，而优美图作为图论的一个重要内容，由于它应用的广泛性，一直是人们研究的热点，也取得了很多研究成果[1-14].1991年，Gnanajoethi提出另一个猜想：“每棵树都是奇优美的”[3]，1982年，Fank Hsu D[4]引入图的强协调标号.由于缺乏一个系统和有力的工具，迄今，只能对一些特殊图探索其优美性、奇优美性及奇强协调性.文献[14]中给出了哑铃图2Cn+{unν1}的奇优美性.本文进一步研究了其优美性和奇强协调性，得到了如下结果.

定理1：当n=4k时，哑铃图2Cn+{unν1}是优美图.

定理2：当n=4k时，哑铃图2Cn+{unν1}是奇强协调图.

定义1[14]：一个简单图G＝（V，E）（V，E分别是G的顶点集与边集）称为优美的，如果存在一个单射f:V（G）→{0，1，2，…，｜E｜}，使得对所有的边uν=e∈E（G），由f*（uν）=|f（u）-f（v）|导出的映射f*:V（G）→{1，2，…，｜E｜}是一个一一对应，f称为G的优美标号.

定义2[4]：对于一个简单图G＝（V，E），若存在映射：f:V（G）→{0，1，…，2｜E｜-1}，满足：（1）f是单射；（2）uν∈E（G），令f（uν）＝f（u）+f（ν），有f是E（G）到{1，3，5，…，2｜E｜-1}的一个一一对应，则称图G是奇强协调图，f为图G的奇强协调标号.

定义3[16，17]：在两个圈Cn（u）=u1u2…unu1和Cm（ν）=ν1ν2…νmν1上，用一条长为l-1的路连接这两个圈的一对顶点ui，νj所得到的图类，称为哑铃图，记为Cn+Cm+Pl.

在本文中，我们记连接两个圈的顶点ui，νj分别为un，ν1（见图1）.本文仅讨论m=n且l=2时的情况，此时哑铃图记为2Cn+{unν1}.为叙述方便，本文规定所讨论的图都是无向简单图，ν既表示点ν，也表示点ν的标号.uν既表示边，也表示该边的标号.点ν2p称为偶点，ν2p-1称为奇点.其他未加说明的定义和符号均来自文献[18].

图1 哑铃图Cn+Cm+Pl

1 定理1的证明

当n=4k时，哑铃图2Cn+{unν1}的顶点数为2n=8k，边数|E|=2n+1=8k+1.当n=4k时，给出哑铃图2Cn+{unν1}的各顶点标号算法A如下：

（1）u2i-1=6k-i+2，其中i=1，2，…，2k；

（2）u2i=2k+i，其中i=1，2，…，k；

u2i=2k+i+1，其中i=k+1，…，2k；

（3）ν2i-1=i-1，其中i=1，2，…，k；

ν2i-1=i，其中i=k+1，…，2k；

（4）ν2i=8k-i+2，其中i=1，2，…，2k.

按照算法A可得以下结果.

引理1：当n=4k时，哑铃图2Cn+{unν1}的顶点集与集合{0，1，2，…，8k+1}构成单射.

证明：当n=4k时，记M是哑铃图2Cn+{unν1}的所有顶点标号集合，由算法A的（1）-（4）易知：

引理2：当n=4k时，哑铃图2Cn+{unν1}的边集与集合{1，2，3，…，8k+1}构成一一对应.

证明：我们把边的标号分为三大类来考虑.

（一）由算法A的（1）（2）可知u1u2…u4ku1中边的标号有以下几种情况：

（1）u2i-1u2i=|6k-i+2-（2k+i）|=4k-2i+2，其中i=1，2，…，k；

（2）u2iu2i+1=|6k-（i+1）+2-（2k+i）|=4k-2i+1，其中i=1，2，…，k；

（3）u2i-1u2i=|6k-i+2-（2k+i+1）|=4k-2i+1，其中i=k+1，k+2，…，2k；

（4）u2iu2i+1=|6k-（i+1）+2-（2k+i+1）]|=4k-2i，其中i=k+1，k+2，…，2k-1；

（5）u4ku1=2k；

（二）由算法A的（2）（3）可知u4kν1=|（2k+2k+1）-（1-1）|=4k+1；

（三）由算法A的（3）（4）可知ν1ν2…ν4kν1中边的标号有以下几种情况：

（1）ν2i-1ν2i=|8k-i+2-（i+1）|=8k-2i+3，其中i=1，2，…，k；

（2）ν2iν2i+1=|8k-i+2-[（i+1）-1]|=8k-2i+2，其中i=1，2，…，k-1；

（3）ν2i-1ν2i=|8k-i+2-i|=8k-2i+2，其中i=k+1，k+2，…，2k；

（4）ν2iν2i+1=|8k-i+2-（i+1）|=8k-2i+1，其中i=k，k+1，…，2k-1；

（5）ν4kν1=|8k-2k+2-（1-1）|=6k+2.

首先，由（一）易知，在u1u2…u4ku1中，各边的标号范围为：

（1）2k+2≤u2i-1u2i≤4k，且标号为偶数，其中i=1，2，…，k；

（2）2k+1≤u2iu2i+1≤4k-1，且标号为奇数，其中i=1，2，…，k；

（3）1≤u2i-1u2i≤2k-1，且标号为奇数，其中i=k+1，k+2，…，2k；

（4）2≤u2iu2i+1≤2k-2，且标号为偶数，其中i=k+1，k+2，…，2k-1；

（5）u4ku1=2k；

由边的标号范围及奇偶性知，在u1u2…u4ku1中各边的标号不相等.

其次，由（二）知，u4kν1=4k+1.

再次，由（三）易知，在ν1ν2…ν4kν1中各边的标号范围为：

（1）6k+3≤ν2i-1ν2i≤8k+1，且标号为奇数，其中i=1，2，…，k；

（2）6k+4≤ν2iν2i+1≤8k，且标号为偶数，其中i=1，2，…，k-1；

（3）4k+2≤ν2i-1ν2i+2≤6k，且标号为偶数，其中i=k+1，k+2，…，2k；

（4）4k+3≤ν2iν2i+1≤6k+1，且标号为奇数，其中i=k，k+1，…，2k-1；

（5）ν4kν1=6k+2.

同样，由边的标号范围及奇偶性知，在ν1ν2…ν4kν1中各边的标号不相等.

最后，由上易知，三类边的标号范围互不重叠，故也互不相等.

综上所述，当n=4k时，哑铃图2Cn+{unν1}中的各边的标号均不相同.即当n=4k时，哑铃图2Cn+{unν1}的边集与集合{1，2，3，…，8k+1}构成一一对应.

定理1：当n=4k时，哑铃图2Cn+{unv1}是优美图.

证明：由引理1、引理2可得当n=4k时，哑铃图2Cn+{unν1}存在优美标号，由定义1，当n=4k时，哑铃图2Cn+{unν1}是优美图，即定理1得证.

2 定理2的证明

当n=4k时，哑铃图2Cn+{unν1}的顶点数为2n=8k，边数为2n+1=8k+1，此时2|E|-1=16k+1.当n=4k时，我们给出哑铃图2Cn+{unν1}的各顶点的标号递推算法B：

（1）u2i-1=2i-2，i=1，2，…，2k；

（2）u2i=2i-1，i=1，2，…，k；

u2i=2i+1，i=k+1，k+2，…，2k；

（3）ν2i-1=4k+2i-2，i=1，2，…，2k；

（4）ν2i=4k+2i+1，i=1，2，…，k；

ν2i=4k+2i+3，i=k+1，k+2，…，2k.

按照算法B得到如下结论.

引理3当n=4k时，哑铃图2Cn+{unν1}的顶点集与集合{0，1，2，…，16k+1}构成单射.

证明记N是当n=4k时，哑铃图2Cn+{unν1}的所有顶点标号集合，由算法B的（1）-（4）易知：

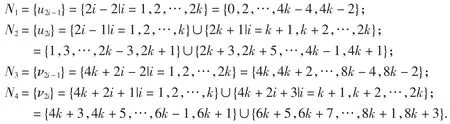
显然，N1，N3中的点全是奇点，其标号全为偶数，N2，N4中的点全是偶点，其标号数全为奇数，且，即当n=4k时，哑铃图2Cn+{unν1}中各顶点的标号均不相同.又所有顶点标号的集合N=N1∪N2∪N3∪N4中最小数是0，最大数是8k +3（当然小于16k+1）.综上，当n=4k时，哑铃图2Cn+{unν1}各顶点的标号均不相同，所以当n=4k时，哑铃图2Cn+{unν1}的顶点集与集合{0，1，2，…，16k+1}构成单射.

引理4哑铃图2Cn+{unν1}的边集与集合{1，3，5，…，16k+1}构成一一对应.

证明由算法B知，我们把边的标号分为三大类来考虑.

（一）由算法B的（1）（2）可知u1u2…u4ku1中边的标号有以下几种情况：

（1）u2i-1u2i=2i-2+2i-1=4i-3，其中i=1，2，…，k；

（2）u2i-1u2i=2i-2+2i+1=4i-1，其中i=k+1，…，2k；

（3）u2iu2i+1=2（i+1）-2+2i-1=4i-1，其中i=1，2，…，k；

（4）u2iu2i+1=2（i+1）-2+2i-1=4i+1，其中i=k+1，…，2k-1；

（5）u4ku1=2·2k+1+（2×1-2）=4k+1.

（二）由算法B的（2）（3）有：u4kν1=2·2k+1+4k+2×1-2=8k+1；

（三）由算法的（3）（4）可知ν1ν2…ν4kν1中边的标号有以下几种情况：

（1）ν2i-1ν2i=4k+2i-2+4k+2i+1=8k+4i-1，其中i=1，2，…，k；

（2）ν2i-1ν2i=4k+2i-2+4k+2i+3=8k+4i+1，其中i=k+1，k+2，…，2k；

（3）ν2iν2i+1=4k+2i+1+4k+2（i+1）-2=8k+4i+1，其中i=1，2，…，k；

（4）ν2iν2i+1=4k+2i+3+4k+2（i+1）-2=8k+4i+3，其中i=k+1，k+2，…，2k-1；

（5）ν4kν1=4k+2·2k+3+（4k+2×1-2）=12k+3.

首先，由（一）易知，在u1u2…u4ku1中，各边的标号均为奇数，都是以4为公差的等

差数列，且范围为：

（1）1≤u2i-1u2i≤4k-3，其中i=1，2，…，k；

（2）4k+3≤u2i-1u2i≤8k-1，其中i=k+1，k+2，…，2k；

（3）3≤u2iu2i+1≤4k-1，其中i=1，2，…，k；

（4）4k+5≤u2iu2i+1≤8k-3，其中i=k+1，k+2，…，2k-1；

（5）u4ku1=4k+1；

由边的标号范围及等差数列的性质知，在u1u2…u4ku1中各边的标号不相等.

其次，由（二）知，u4kν1=8k+1.

再次，由（三）易知，在ν1ν2…ν4kν1中，各边的标号也均为奇数且都是以4为公差的等差数列，且范围为：

（1）8k+3≤ν2i-1ν2i≤12k-1，其中i=1，2，…，k；

（2）15k+5≤ν2i-1ν2i≤16k+1，其中i=k+1，…，2k；

（3）8k+5≤ν2iν2i+1≤12k+1，其中i=1，2，…，k；

（4）12k+7≤ν2iν2i+1≤16k-1，其中i=k+1，…，2k-1；

（5）ν4kν1=12k+3.

同样，由边的标号范围及等差数列的性质知，在ν1ν2…ν4kν1中，各边的标号不相等.

最后，由上易知，三类边的标号范围互不重叠，故也互不相等.

综上所述，当n=4k时，哑铃图2Cn+{unν1}各边的标号均不相同，且全为奇数.即当n=4k时，哑铃图2Cn+{unν1}的边集与集合{1，3，5，…，16k+1}构成一一对应.

定理2：当n=4k时，哑铃图2Cn+{unν1}是奇强协调图.

证明：由引理3、引理4及定义2可知，定理2成立.

3 注记

按照算法A、B，分别得到哑铃图2C8+{u8ν1}的优美标号（图2）和奇强协调标号（图3）如下：

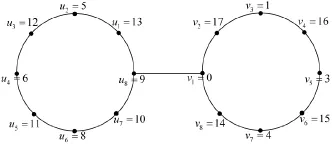
图2 哑铃图2C8+{u8ν1}的优美标号

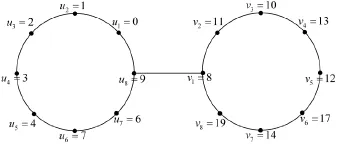
图3 哑铃图2C8+{u8ν1}的奇强协调标号

[1]Ringel G.Problem 25，in：theory of graphs and its application[J].Proc Symposium Smolenice，1963，1263：162-167.

[2]Gallian J A.A dynamic survey of graph labeling[J].The Electronic Journal of Combinatorics，2009，16（6）：1-219.

[3]Gnanajothi R B.Topics in graph theory[D].India：Madurai Kamaraj University，1991.

[4]Hsu D F.Harmonious labelings of windmill graphs and related graphs[J].Journal of Graph Theory. 1982，6（1）：85-87.

[5]林育青.关于图Pn3的优美性[J].华南师范大学学报：自然科学版，2000（3）：21-24.

[6]邓怀敏，林育青.关于图Pn3的优美标号[J].新疆大学学报：自然科学版，2000，17（2）：12-16.

[7]林育青.一类图的优美性[J].云南师范大学学报：自然科学版，2004，24（4）：15-19.

[8]林育青.Cn与1Cn的优美标号[J].安徽大学学报：自然科学版，2007，32（2）：13-16.

[9]林育青，钟发胜，童细心，等.图Pn3的奇优美标号算法[J].数学理论与应用，2013，33（4）：29-34.

[10]林育青，张玲瑛，钟发胜，等.关于奇优美图及奇强协调图的一点注记[J].贵州师范大学学报：自然科学版，2014，32（2）：43-46.

[11]张玲瑛，林育青，钟发胜，等.关于图2×Cn的标号[J].北华大学学报：自然科学版，2014，15（2）：174-178.

[13]童细心，林育青，钟发胜.圈Cn的奇优美性和奇强协调性[J].西南师范大学学报：自然科学版，2014，39（8）：10-13.

[14]刘家保，王林，陆一南.双圈图G（n，m）的奇优美标号及其算法[J].合肥工业大学学报：自然科学版，2012，35（5）：708-710.

[15]马克杰.优美图[M].北京：北京大学出版社，1991.

[16]Ali M，Ali G，Ali U，et a1.On cycle related graphs with constant metric dimension[J].Open J Discrete Math，2012，2（1）：21-23.

[17]Tang Z K，Huang G H，Jiang X J，et al.The metric dimension of dumbbell-shape graph[J]. Journal of Natural Science of Hunan Normal University，2013，36（6）：7-10.

[18]Bandy J A，Murty U S R.Graph theory with application[M].New York：American Elsevier Publishing Co Inc，1976.

Gracefulness and Odd Strong Harmoniousness of A K ind of Dumbbell-Shape Graphs

TONG Xixin
（Department of Natural Sciences,Shantou Polytechnic,Shantou 515041,Guangdong,China）

Gracefulness and odd strong harmoniousness of dumbbell-shape graphs have been studied.Dumbbell-shape graphs are shown to be graceful and odd strongly Harmonious when n=4k.

dumbbell-shape graph；graceful graph；odd strongly harmonious graph

O 157.5

A

1001-4217（2015）02-0038-06

2014-11-05

童细心（1979-），男，湖南岳阳人，讲师.研究方向：图论.E-mail：txx2486@126.com

汕头职业技术学院重点资助课题（SZK2013Z1）