Stein岭型主成分估计下多个数据删除模型的强影响分析
朱宁,严冠东,刘庆华
(桂林电子科技大学数学与计算科学学院,广西桂林541004)
Stein岭型主成分估计下多个数据删除模型的强影响分析
朱宁,严冠东,刘庆华
(桂林电子科技大学数学与计算科学学院,广西桂林541004)
基于Stein岭型主成分估计下研究多个数据删除模型,探讨数据删除模型估计量的有关性质,并给出了多个数据删除模型的CRi统计量、APi统计量、Di统计量的新表达式.
Stein岭型主成分估计;多个数据删除模型;多个强影响点;诊断统计量
0 引言
考虑一般线性模型:

其中,y为n×1阶观测向量,X为n×p阶列满秩设计阵,β为p×q阶未知参数向量,ε为n×1阶随机误差,I为n阶单位矩阵.
在统计诊断中,通常需要寻找和判断对回归系数影响较大的数据点,如果删除这些强影响点,回归模型的系数会受到很大影响,数值会发生较大变化.这时候需要检验是人为因素造成还是数据集本身造成的.解决这类问题的方法,在统计诊断学中称为影响分析.为了研究数据集每组数据点对模型的影响程度大小,为此通常采用数据删除模型.
记i的m个指标集为J={i1,i2,…,im},对于模型(1)中,把J中的指标对应的数据删除以后,与模型(1)相对应的数据删除模型的各个量分别记为X(J),y(J)和ε(J),其中y(J)和ε(J)为(n-m)维向量,X(J)为(n-m)×p阶矩阵,则此时的数据删除模型表示为

此时的最小二乘估计为

文献[1]在最小二乘估计下讨论数据删除模型的影响度量矩阵和高杠杆点度量;文献
[2]在广义岭估计下讨论删除单个点数据删除模型的影响度量和高杠杆点度量;文献[3]在广义岭估计下讨论删除单个点数据删除模型的影响度量和高杠杆点度量.本文在前人基础上,推广到删除多个数据点数据删除模型,定义新的影响度量矩阵HJ和数据删除模型高杠杆点度量意义,同时把文献的结论推广到一般形式.
1 主要结果
考虑模型(1)和(2)定义新的影响度量矩阵为

其中XJ为删除数据矩阵.显然HJ为m×m阶矩阵,它的元素为

当i,k埸J时,所有的hik正好构成了模型(2)的帽子矩阵,即

可得

首先给出引理1.
引理1[4]在模型(1)下提出了未知参数β的Stein岭型主成分估计,即在岭-压缩组合估计的基础上再进行Stein估计,叫做Stein岭型主成分估计(有偏岭-压缩组合估计),记作:,
其中,
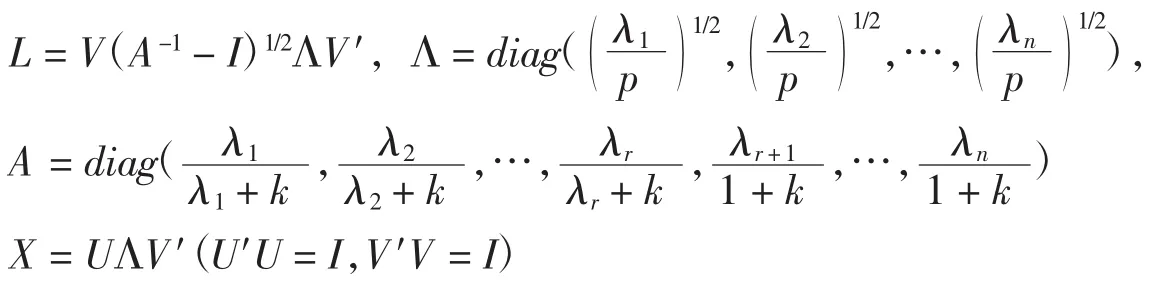
证明:


性质2在线性模型y=Xβ+ε,ε~N(0,σ2I),删除数据集J={i1,i2,…,im}得到模型y(J)=X(J)β(J)+ε(J),由Stein岭型主成分估计,则y赞J可以表示为和yJ的线性组合.
证明:

性质3在线性模型y=Xβ+ε,ε~N(0,σ2I),删除数据集J={i1,i2,…,im}得到模型y(J)=X(J)β(J)+ε(J),由表示数据删除模型未知参数β的Stein岭型主成分估计,则删除数据集J={i1,i2,…,im}的预测残差和普通残差的关系有:

性质4线性模型y=Xβ+ε,ε~N(0,σ2I),删除数据集J={i1,i2,…,im}得到模型y(J)=

当删除了数据集J中m个点时,相对应的HJ就是一个高杠杆点度量,HJ越大,删除后的数据对原模型的影响就越大.
在多个数据删除模型中,为了研究数据集与模型的拟合程度,下面对Hii(J)进行探讨,当矩阵X有一列为常数1时,考虑

其中1为所有元素为1的相应维数的列向量.


从上述内容可以看出,若删除m个数据点后,其他样本点中心的距离越远,Hii(J)越大,因而Hii(J)是一个度量m个数据点对模型影响大小的统计量,我们定义为高杠杆值.

所以,性质5是把单个数据删除模型推广到m个数据删除模型的高杠杆度量的一般情况.
2 统计量
2.1 PRESS统计量
Allen[5](1971)提出PRESS统计量,用来度量模型拟合的好坏.
2.2 协方差比统计量
性质4在Stein岭型主成分估计下,协方差比统计量


引理2[7]模型Y(J)=X(J)β(J)+ε(J)中β和σ2的最小二乘估计与模型(1)的相应估计有如下关系:,其中.
由于

2.3 AP统计量
AP统计量是由Andrew,D.F.和Pregibon,D.[8]提出的,在协方差比的基础上进一步考虑对的影响.Drape和John[9]对AP统计量进行分解,提出探测异常点的统计量新形式.
引理3[7]模型y(J)=X(J)β(J)+ε(J)中β和σ2的最小二乘估计与模型(1)的相应估计有如下关系:.
证明:

结论得证.
定理2设X**=(X*,Y),X*=(X,Y),则AP统计量可以表示为

2.4 Cook统计量
Cook统计量是Cook[10](1977)提出Cook统计量作为度量第i个数据点影响大小的数量指标.
引理4[7]广义Cook统计量为.
定义3在Stein岭型主成分估计下,定义Cook统计量为

定理3在Stein岭型主成分估计下,Cook统计量可表示为.
证明:

推论在Stein岭型主成分估计下,Cook统计量可表示为
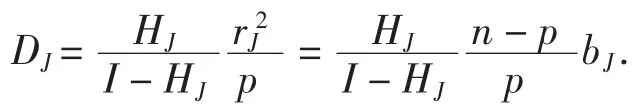
证明:由引理和定理3可得,
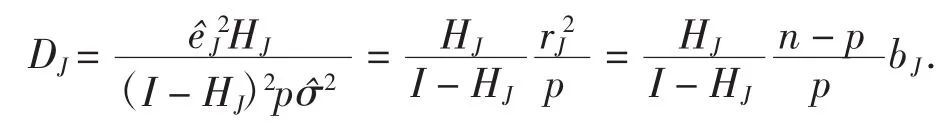
[1]杨虎,邵华.线性回归诊断中的高杠杆点度量[J].工程数学学报,2009,26(1):123-132.
[2]钱峰,石丽娟.数据删除模型对于广义岭估计的影响[J].南通大学学报:自然科学版,2008,7(1):75-78.
[3]朱宁,黄黎平,李绍波,等.数据删除模型下的高杠杆点度量[J].统计与决策,2012(5):32-34.
[4]朱宁,李建军,李兵.一种有偏岭-压缩组合估计的新形式[C]//曾玲,刘克.第八届中国青年运筹信息管理学者大会论文集.桂林:桂林电子科技大学,2006:287-290.
[5]Allen D M.Mean square error of prediction as a criterion for selecting variables[J].Technometrics,1971,13(3):469-475.
[6]张尧庭,方开泰.多元统计分析引论[M].北京:科学出版社,1982.
[7]韦博成.统计诊断引论[M].南京:东南大学出版社,1991.
[8]Andrews D F,Pregibon D.Finding the outliers that matter[J].J R Statist Soc B,1978,40:87-93.
[9]Draper N R,John J A.Influence observations and outliers in regression[J].Technometrics,1981,23(1):21-26.
[10]Cook R D.Detection of influential observations in linear regression[J].Technometrics,1977,42(1):65-68.
Strong Im pact Analysis of M ultip le Data Delete M odel Based on Stein Ridge and Principal Com ponents Estimator
ZHU Ning,YAN Guandong,LIU Qinghua
(School of Mathematics and Computing Science,Guilin University of Electronic Technology, Guilin 541004,Guangxi,China)
Strong impact analysis of multiple data delete model based on stein ridge and principal components estimator is studied.A strong impact on the analysis model under biased estimator is proposed.The property of estimators of the data deletion model is also discussed.Besides,the new expressions of CRi,APiand Dibased on multiple data delete model,are given.
stein ridge and principal components estimate;multiple data deletion model;multiple influential point;diagnostic statistics
O 212.1
A
1001-4217(2015)02-0020-08
2014-10-13
朱宁(1957-),男,湖南宁乡人,教授,研究方向:线性统计模型.E-mail:znqx@guet.edu.cn
桂林电子科技大学研究生创新项目(GDYCSZ201471)

