确定型多局域世界图中Agent最优策略解析
郑 湛, 郑小京, 徐绪松
(1. 武汉纺织大学, 武汉 430073; 2. 哈尔滨商业大学, 哈尔滨 150076; 3. 武汉大学, 武汉 430072)
确定型多局域世界图中Agent最优策略解析
郑 湛1, 郑小京2*, 徐绪松3
(1. 武汉纺织大学, 武汉 430073; 2. 哈尔滨商业大学, 哈尔滨 150076; 3. 武汉大学, 武汉 430072)
在短的time-scale中,在一个确定的系统拓扑结构下,用解析的方法确定复杂管理系统Agent的最优策略.构建了一个确定型多局域世界图博弈模型,对确定型多局域世界图,分两种情况——局域内Agent的合作博弈和局域之间的非合作博弈,讨论Agent行为均衡解;并将局域内Agent的合作随机微分博弈与局域Super-Agent之间的非合作随机微分博弈进行了耦合.以确定复杂管理系统Agent的最优策略.最后讨论了最优策略的稳定性.
确定型; 多局域世界图; Agent的最优策略; 随机微分博弈
0 引 言
21世纪,复杂的管理系统普遍存在于现实生活中,如房地产、供应链、区域经济、金融市场等,这类复杂管理系统,具有如下特征:1)系统具有一定的拓扑结构,人的行为与系统拓扑结构共同演化.2)系统由若干个相互作用的子系统构成,每一个子系统的主体都为了一个共同的目标而进行合作,而不同的子系统之间又为了自身利益最大化而竞争.3)当时间短时(短的time-scale),系统中各个主体间的相互作用发生在一个确定的系统拓扑结构中,在系统中存在着合作与竞争两种情况,经过相互作用,系统中的成员都能找到一个最优策略.4)随着时间的增长,系统自身的特性在不断变化,为了提升自身的综合竞争能力以及盈利能力,或与其他主体创建新的关系,或断开现有的联系.当时间长时(长的time-scale),主体的最优策略将随着一个确定拓扑结构到下一个确定拓扑结构不断发生变化,没有一个确定的最优策略,但是,最优策略的分布特征可能存在.
鉴于复杂管理系统的复杂性,学者主要采用仿真的方法对复杂管理系统中的最优策略进行探索,分析系统特征以及系统与环境之间的相互关系,并获得了一定的结论[1-5].由于仿真对于系统内部运行机制的处理,以及规则的发现具有一定的局限性,为了解决这一问题,笔者将基于人的行为的复杂管理系统抽象成多局域世界图(称为Super-Agent,其中的决策主体为Agent),采用随机微分博弈,研究系统中Agent的最优策略[6-8].本文主要研究具有短的time-scale特征的、确定的系统拓扑结构下的Agent最优策略.长的time-scale特征的、变化系统结构下的Agent最优策略的分布特征将在下篇论文中研究.
本文的研究思路是:首先给出预备知识,然后对确定的系统拓扑结构构建一个确定型多局域世界图博弈模型,再对确定型多局域世界图,分两种情况——局域内Agent的合作博弈和局域之间的非合作博弈,讨论Agent行为均衡解,获得合作博弈的最优策略,非合作博弈的Nash均衡策略.并将局域内Agent的合作随机微分博弈与局域Super-Agent之间的非合作随机微分博弈进行耦合,即将各个局域收益进行合理分配.最后讨论了最优策略的稳定性.
1 预备知识
1.1 定义
图的子图Ci∈(C1,C2,…,Cm)被定义为局域(Ci实际上是一个随机矩阵)[9].如果
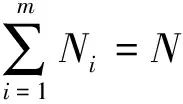
2)对于任意1≤i,j≤s,i≠j,

1.2 假设
假设1 假设基于人的行为的复杂管理系统由若干个子系统构成,这些子系统称之为局域.这些局域足够大,使得每一个局域中可以容纳足够多数量的决策主体;同时,假定这些局域又足够小,使得有足够数量的局域在不断进行交互作用.
假设2 在一个短的时间范围(time-scale)内各个局域中的Agent之间以合作博弈机制进行相互作用,在追求区域整体利益最大化的基础上将收益进行合理分配;而对于不同的、相互联系的局域,他们之间按照非合作博弈机制进行相互作用.
对应于确定的拓扑结构的Agent合作/非合作博弈,系统的Agent行为有一个动力学方程,该方程涉及到系统的Agent策略的各个参数.该方程收敛到稳态状态时的最短时间为短的time-scale的下确界.
从假设1-假设2说明如下两点:
1)在复杂管理系统中,有足够多的主体在相互作用,参与管理组织的运作.这一系统由两个层次构成,上层称之为Super-Agent(局域),下层称之为Agent.每一个Super-Agent中还有若干个不同的Agent.
2)同一局域内的Agent之间的相互作用关系是合作博弈,而不同局域之间的相互作用关系是非合作博弈.局域内合作博弈的目的是为了达到局域内Agent行为的协调化或同步,从而提高整个局域的综合竞争能力.而不同局域之间非合作博弈,将使得各个局域之间产生竞争,于是,系统行为之间存在差异,这种差异使得系统不断的创新.
2 博弈模型: 确定型多局域世界图
本文将确定的拓扑结构抽象为一个确定型多局域世界图,各个Agent之间的博弈关系抽象成一个多局域世界图中的随机微分博弈模型,通过解析这一模型,确定系统中Agent的最优策略.
将复杂管理系统中Agent相互作用之间的关系记为图G,设图G由m个子图构成(这些子图都应该属于密集图[10],在文献[11]的方法上实现分割),子图i中的第j个Agent为ji,则各个Agent之间相互作用的拓扑结构为其邻接矩阵G=(G1,G2,…,Gm).
下面分别讨论局域之内Agent的合作博弈、局域之间Agent的非合作博弈、以及Agent之间的合作-非合作博弈.
考虑系统中每个Super-Agent的状态约束,得随机偏微分方程
(1)
其目标方程为

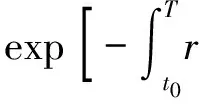
(2)
方程(2)假定了行为的贴现因子函数为指数分布,大多数管理系统都满足这一特征.
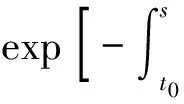
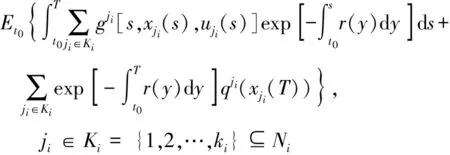
(3)
系统状态及其变化为
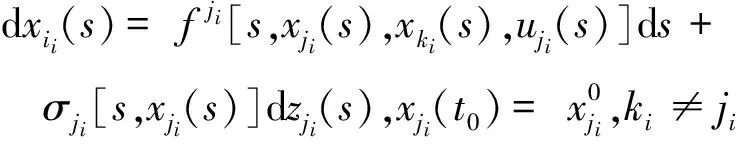
3 确定型多局域世界图中Agent行
为均衡解1: 局域内Agent的合作
博弈
对于第2节描述的静态复杂管理系统中Agent之间的博弈,需要确定以下两个重点:1)最优化每一个局域的收益;2)对于任意的局域,需将获得的最优化收益进行合理的分配.这两个特征将会使得该复杂管理系统具有长期持续的综合竞争能力.
按照第1节中的假设,不同的Super-Agent之间的相互作用是非合作随机微分博弈驱动,同一局域内的Agent之间的相互作用是以合作随机微分博弈驱动.第3节和第4节将针对这两种不同的行为进行较为深刻的分析.
3.1 子系统的收益最大化
考虑任意一个局域i的合作随机微分博弈,其局域的系统目标为
(5)
系统状态及其变化为
(6)
子系统收益最大化问题,有两个问题需要解决,第一,是确定局域的最优策略;第二,是在一个局域内将各个Agent的利益进行公平的分配[10-14].这两个问题都是一个随机优化问题.不妨记模型(5)-(6)的最优控制为Γ[Ni;t0,x0].
定理1给出了局域的最优策略,解决了子系统收益最大化问题的第一个问题.

其边界条件为

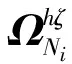
注释1 1)由于合作随机微分博弈模型(5)-(6)的最优解非常难获得,需要将这一博弈分解成两部分来求解,第一部分就是整个局域的收益最大化,第二部分就是局域内各个Agent所分配的收益合理.第一步主要描述的是集体理性约束条件,本质上就是一个随机微分优化问题,定理1将这一问题的最优解转换为一个PDE的解,通过求解这一方程,就可以知道,该局域的最大收益,以及对应的Agent的最优策略状态.
2)所谓的策略,其实就是各种资源在某一个时间点上的最优配置,这些资源包括人、资金、商品、信息等等.最优策略与时间有关系,因此得到的最优策略应该是一个多维函数形成的轨迹.
3)系统收益最优,实际上是整体收益最大,这时所得到的资源量等于局域内所有Agent的资源量的总和,称之为集中决策.
4)如果一个经济或管理组织,需要最小的努力在最大程度上实现某一目标的价值,这个组织就需要将自己的资源合理的分配,达到一个最优结构.这一最优结构的资源大小可通过定理1计算.
下面探讨第二个问题.
方程(6)中考虑了Agentji与在同一局域内的其他Agent之间的相互作用,这一相互作用依赖于系统的拓扑结构,当且仅当矩阵元素cjiki=1时,Agentji与Agentki之间的相互作用才能体现出来,才能形成合作关系,获得多种合作联盟所导致收益公平分配下的最优策略.
同理,可以确定局域内,Agent之间相互作用而形成的各种联盟Ki最优收益时对应的各个Agent的策略,其对应的方程为
(7)
(8)
模型(7)-(8),可以得到最优策略.
定理2给出了在一确定局域内,由于Agent之间相互作用而形成的各种联盟Ki最优收益时的最优策略,这就解决了子系统收益最大化问题的第二个问题.
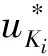

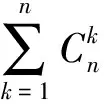
2)每一个Agent可以参加任意的一个联盟,当k=1时,这一联盟只有一个Agent.在不同的联盟中,Agent可以获得不同的收益,Agent通过综合比较,确定自己能够获得最大收益的条件.当然,参加任何一个联盟与别的Agent进行合作时所得到的收益应该不低于这些最大收益的平均值.
3)在一个经济或管理系统中,局域中的参与者都可以参加任何一个联盟,从而获得一定的收益.获得的最大收益、最优的策略以及对应的联盟,可以通过定理2获得.与定理1一样,最优策略与时间相关,其轨迹是一个函数.
4)局域中Agent参加联盟这一假设是必要的,描述了一种虚拟的联盟形式.通过定理2,可以知道Agent所有可能的收益与策略的集合(局部最优条件)所对应的一个决策(分散决策).
定理2是Agent在局域内分配收益时的基础.
3.2 局域内收益的Shapley分配
对于局域内Agent收益的分配,需要达到公平、合理、公正的效果,为此,提出以下条件:(1)所分配的收益之和必须等于局域最大收益;(2)对每一个Agent,参与合作所分配的收益应该不小于不参与合作所得到的收益.前者称作为集体理性,后者称之为个体理性.对局域内所有的Agent,他们都在力争获得更大的分配收益,从而引发了合作博弈.因此,合作博弈的关键在于设计一种合理的分配机制,使得每个Agent感受“合理”.
本文将采用动态Shapley值法[15-21],对任意局域内的Agent的收益进行分配,并确定其对应的策略.下面根据研究对象,给出对应的条件.
条件1
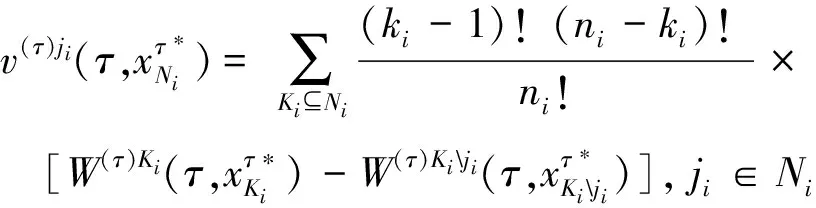
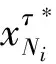
满足下列分配向量的基本属性:
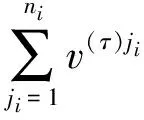
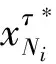
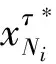
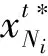

其中Kiji是{ji}的补集.
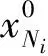
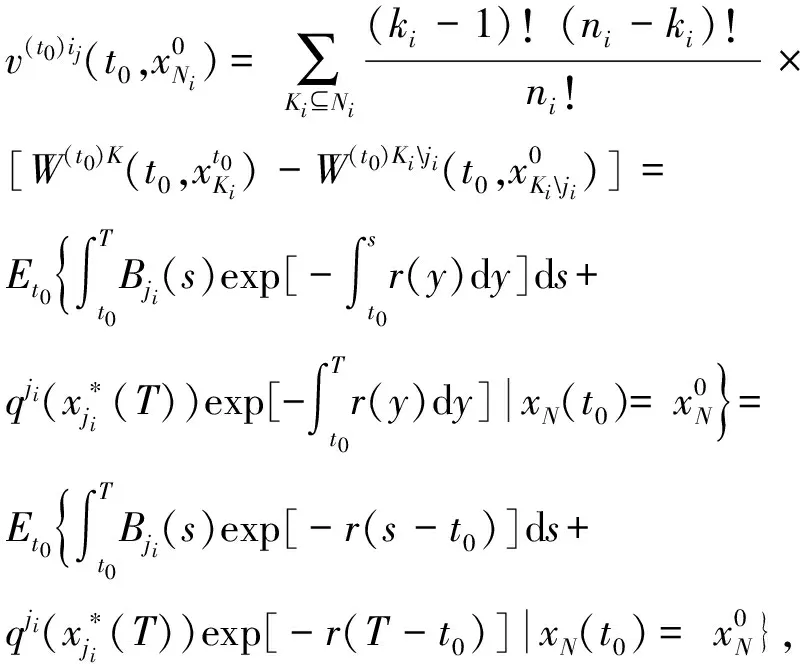
ji∈Ni
(9)
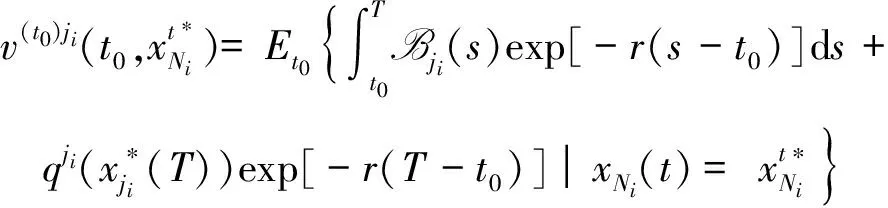
(10)

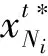
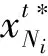
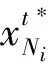
(11)
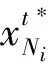
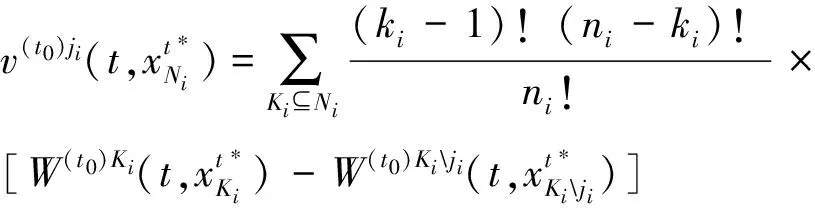
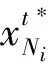
为了实现这一构造,给出定理3.
定理3Agentji∈Ni在时间τ∈[t0,T]的暂静态分配收益等于
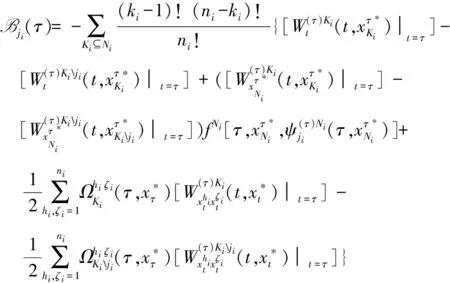
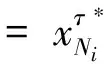
(证明略)
根据以上分析,得到1)Agentji将自己的收益水平努力提高到gji[s,xji,uji],且qji(xji)正相关与收益xji.2)Agent能够从与其他Agent形成联盟的收益函数中获得的关键收益将会导致

L⊂K⊆N
其中,KL是L在K中的补集.
定理3给出了Agent的暂静态分配收益.为使得收益在Agent中合理分配,定理4将进一步给出了满足条件1的Agent暂静态补偿收益.
注释3 1)当一个局域收益达到最大时,即定理1得以满足时,将使得整个局域的最大收益在局域内各个Agent中合理分配.
2)对于任何一个Agent,进入一个局域并能与其他Agent合作的条件是:参加合作得到的收益不低于独立实现目标所得到的收益.这要求每一个Agent努力发挥自己的核心竞争力,并在定理3设计的机制下,通力合作,从而不仅使得整体的收益最大,而且使得自己的收益大于独立运营时得到的收益.体现了合作随机微分博弈的意义.
3)与定理1、3.2节一致,分配到的收益是关于时间的一个映射,也是动态的,并且形成了一个最优分配的轨迹.
定理4Agentji∈Ni在时间τ∈[t0,T]能够导致条件1的暂静态补偿收益为
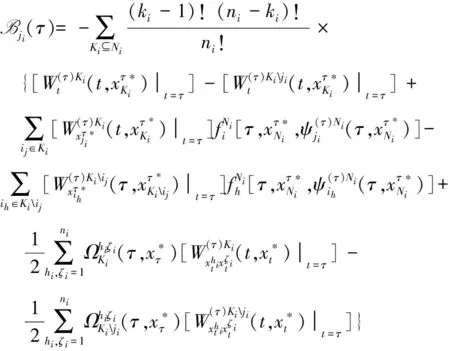

(证明略)

注释4 定理4描述了当系统中各个Agent的约束有差异的情况,其他的管理方面的解释与定理3相同.
定理3与4描述了具有同质指数分布这一特征的贴现因子函数,在系统中、同一局域内各个Agent利益分配及补偿的情况.
4 确定型多局域世界图中Agent行为 均衡解2: 局域之间Agent的非合
作博弈
4.1 非合作博弈下Super-Agent的均衡策略
本文将每一个局域抽象成为一个Super-Agent,假设整个系统可以分解成m个局域.按照前面的假设1-假设2, Super-Agent之间的相互作用是非合作随机微分博弈Γ,本文将构造非合作随机微分博弈模型.
对于任意的Super-Agenti,其目标可以确定为
i∈M
(12)
对应的约束条件为 dxi(s)=fi[s,xi(s),ui(s)]ds+σi[s,xi(s)]dzi(s),
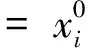
(13)
对于每一个Super-Agent,他们之间的非合作随机微分博弈应该存在一个Nash均衡点,每个Super-Agent都会有自己的Nash策略,及其对应的收益.

Vi(T,x)=qi(x),i∈N
(证明略)
4.2 Super-Agent的非合作与Agent的合作
耦合
第3节和第4.1节分别给出了局域内的Agent合作博弈的最优策略,以及Super-Agent非合作博弈的Nash均衡策略.第4.1节中,各个Super-Agent达到均衡状态时的局域获得的收益是Vi(t,x)∶[t0,T]×Rm→R,其中i∈M.显然,这一收益并非将某一个Super-Agent孤立地进行优化之后获得的收益,也就是并非Wi(t,x)∶[t0,T]×Rm→R,其中i∈M.但是在第3节的分析中,Agent的策略及收益来自于Wi(t,x)∶[t0,T]×Rm→R,并非是Vi(t,x)∶[t0,T]×Rm→R,即非合作与合作存在偏差.因此必须纠正这一偏差,称之为非合作与合作的耦合.
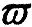
命题1 设(X,d)是完备尺度空间,(Y,C)是Hausdorff序拓扑空间且c0∈intC.设f∶X→Y是向量值映射且C-有下界.设对给定的ε>0和每一个x∈X,集合

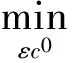
1)f(xε)≤Cf(x0)

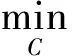


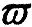
定理5 存在使得V(s,x,u)=φ(W(s,x,u))成立的函数φ(x),对于贴现因子函数满足同质指数分布的经济与管理复杂自适应系统,满足
如果Γ为一个无限维反馈博弈,则φ(t,x)=exp[-r(t-t0)]x;
如果Γ为一个有限维反馈博弈,则φ(t,x)=o(exp[-r[t-t0]]xq),且0 (证明略) 定理5将局域内Agent的合作随机微分博弈与局域Super-Agent之间的非合作随机微分博弈进行了耦合.通过耦合便可以直接将局域最优化的结果修订为局域Super-Agent之间的非合作随机微分博弈的Nash均衡解,将其在局域内进行分配,从而实现复杂管理系统(多局域世界图中合作-非合作博弈为相互作用机制)Agent的最优策略及收益. 注释5 1)通过定理5,可以知道在合作与非合作随机微分博弈混合作用下,系统中任何一个Agent的策略与对应的最大收益的表达方式. 2)定理5告诉人们,系统中任意一个Agent的最优策略与最大收益依赖于以下特征:局域内合作随机微分博弈的收益与策略、实现目标时的折扣因子、目标函数以及自身资源的动力学方程,也就是任何一个Agent的最优策略与最大收益依赖于自身的特点. 3)从管理意义上讲,通过调查可以得到每一个Agent资源的行为规则、目标函数以及初始条件,于是可以通过定理1~定理5便可以确定出该Agent的最优策略及其最大收益,以指导整个管理系统的决策. 随机微分博弈是一个动态博弈,在系统随着Agent之间的相互作用,以及受外部环境干扰时,将会发生动态变化,当且仅当系统中的Agent行为(策略)收敛到一个比较恒定的值时,系统趋于稳定,行为才能被称之为“确定”的.这时只要出现“不和谐”的因素,将会使得整个系统发生相变. 在第3节和第4节对优化问题、博弈问题求解的过程中,笔者将其转化为一系列Bellman簇的方程,显然,这些方程解的收敛性直接决定了博弈解的收敛性,因此,Agent的相互作用经过某一段特定长的时间之后,其策略趋于一个稳定的值. 因为收敛特性由描述系统特性的Agent行为的约束条件,即状态动力学方程所对应的偏随机微分方程的收敛特性所决定[24].因此可以将问题转换为对Agent状态动力学方程吸引子的解析. 对于一个一般系统 d[x(t)-G(xt)]=f(t,xt)dt+g(t,xt)dW(t) (14) 定义1 严格正函数ψ(t)为ψ-函数,如果满足ψ(0)=1,ψ(∞)=0,且对任意t≥-τ,ψ′(t)<0. (15) (16) 其中x(t)=x(t,ξ)是方程(14)的解. 引理2 不妨设存在常数κ∈(0,1)使得 |G(φ)|≤κ‖φ‖ (17) 对于所有的φ∈C([-τ,0],Rn).令 t≥0 (18) 下面定义其对应的吸引子. (19) (20) 引理3 设(H)成立,假定存在函数V(t,x)∈C1,2(R+×Rn,R+),γ(t)∈L1(R+,R+),u1(x),u2(x)∈C(Rn,R+)及∶[-τ,0]→R+,使得(s)ds=1.同时存在常数p≥1和c>0,使得 (21) 对于所有(t,φ)∈R+×C([-τ,0],Rn).假设 u(x)=u1(x)-u2(x)≥0,对所有x∈Rn,有 如果α=0, (22) 如果α>0, c|x|p≤V(t,x) (23) 则ker(u)={x(t)∈Rn∶u(hα(t))=0}≠Ø,即 (24) 引理3表明hα(t)将以概率1无限次访问ker(u)的邻域,也就是说,ker(u)吸引hα(t)无限次,致使一些学者认为ker(u)是hα(t)的弱吸引子.然而,这并不保证hα(t)最终被ker(u)吸引. (证明略.强收敛性见定理6). 在引理3条件下,假定 (证明略). 以联盟Ki⊆Ni为例描述同质指数分布为贴现因子的对应的方程,具体结果参见定理1.当且仅当定理1对应的Bellman方程的解收敛时,系统内Agent的Pareto-Nash最优策略才能收敛到其吸引子.下面,确定这三个系统对应的Lyapunov函数L(W(t,x)). (25) 令ψ(t)=exp[-r(t-t0)],由式(25)知道 (26) 不妨令p=1,φ(t)=x(t),根据x(t)的特性,可知 这种情况下,系统最优策略的收敛如图1所示. 这就是说,在最优控制综合函数的作用下,系统从任意初态开始,以及遇到任意的扰动,它都以最优的方式运行至终端x(T),即获得的最优策略能够收敛于吸引子. 图1 随机扰动下系统中Agent最优策略的稳定性 本文研究基于人的行为的复杂管理系统.在短的time-scale中,如何确定在一个确定的系统拓扑结构下Agent的最优策略.提出了一个确定型多局域世界图博弈模型,并对确定型多局域世界图,分两种情况讨论Agent行为均衡解:(1)局域内Agent的合作博弈;(2)局域之间的非合作博弈.分别获得局域内的Agent基于合作博弈的最优策略,基于非合作博弈的Nash均衡策略.并将局域内Agent的合作随机微分博弈与局域Super-agent之间的非合作随机微分博弈进行了耦合,将收益在局域内合理分配.最后讨论了最优策略的稳定性.本文与以往研究不同之处是提出了在短的time-scale中,一个确定的系统拓扑结构下Agent的最优策略确定的解析方法. 本文对在短的time-scale中Agent的最优策略进行了分析,这只是经济与管理复杂自适应系统的开端.正如在假设中提出的那样,可以看出,本文所研究的经济与管理复杂系统是从时间与空间两个维度按照不同粒度对系统进行分割的,即从空间上按照“物以类聚、人以群分”的思想分割成不同的子系统(从大的空间-scale看,小的空间scale被压缩成一个个体);从时间上按照系统结构的固定与变化将系统发展分割成短的time-scale和长的time-scale两种(从长的time-scale看,短的time-scale被压缩成一个时间点).由于篇幅限制,本文并没有针对长time-scale中Agent的最优策略演化特征进行分析,关于在长time-scale中变化系统结构下Agent最优策略的分布特征,将在后续的文章中给予翔实的分析. [1]Ke Hu, Tao Hu, Yi Tang. Cascade defense via control of the fluxes in complex networks[J]. J. Stat. Phys., 2010, 141: 555-565. [2]杨 孟, 傅新楚, 吴庆初. 复杂网络上带传播媒介SIS模型的全局稳定性[J]. 系统工程学报, 2010, 25(6): 767-773. Yang Meng, Fu Xinchu, Wu Qingchu. Global stability of SIS epidemic model with infective medium on complex networks[J]. Journal of Systems Engineering, 2010, 25(6): 767-773. (in Chinese) [3]Gao Z, Kong D, Gao C. Modeling and control of complex dynamic systems: Applied mathematical aspects[J]. Journal of Applied Mathematics, 2012, 2012(4): 1-18. [4]Sethna J P. Entropy, Order Parameters, and Complexity[M]. Oxford: Oxford University Press, 2006. [5]Cao W, Chen G, Chen X. Optimal tracking agent: A new framework of reinforcement learning for multi-agent systems[J]. Concurrency and Computation: Practice and Experience, 2013, 25: 2002-2015. [6]蒋国银, 胡 斌. 集成博弈和多智能体的人群工作互动行为研究[J]. 管理科学学报, 2011, 14(2): 29-41. Jiang Guoyin, Hu Bin. Study on interaction between group and work based on game and multi-agent[J]. Journal of Management Sciences in China, 2011, 14(2): 29-41. (in Chinese) [7]龚日朝. 基于秩依期望效用理论的鹰鸽博弈均衡解分析[J]. 管理科学学报, 2012, 15(9): 35-45. Gong Rizhao. Nash equilibrium of hawk-dove game based on rank-dependent expected utility theory[J]. Journal of Management Sciences in China, 2012, 15(9): 35-45. (in Chinese) [8]王先甲, 全 吉, 刘伟兵. 有限理性下的演化博弈与合作机制研究[J]. 系统工程理论与实践, 2011, 30(增刊1): 82-93. Wang Xianjia, Quan Ji, Liu Weibing. Study on evolutionary games and cooperation mechanism within the framework of boundedrationality[J]. Systems Engineering: Theory & Practice, 2011, 30(Sup1): 82-93. (in Chinese) [9]Newman M E J. The structure and function of complex networks[J]. SIAM Review, 2003, 45(2): 167-256. [10]陶少华, 张向群. 复杂网络自相似特征演化模型研究[J]. 计算机工程, 2012, 38(1): 197-199. Tao Shaohua, Zhang Xiangqun. Research on self-similarity characteristic evolution model of complex network[J]. Computer Engineering, 2012, 38(1): 197-199. (in Chinese) [11]Nepusz T, Negyessy L. Reconstructing cortical networks: Case of directed graphs with high level of reciprocity[M]. In: BelaBollobas, Robert Kozma, DeasoMiklos. Handbook of large-scale random networks. Hungary: Springer. 2008: 325-368. [12]Cajueiro D O, Andrade R F S. Controlling self-organized criticality in complex networks[J]. The European Physical Journal B, 2010, 77: 291-296. [13]王 龙, 伏 锋, 陈小杰, 等. 复杂网络上的群体决策[J]. 智能系统学报, 2008, 3(2): 95-107. Wang Long, Fu Feng, Chen Xiaojie, et al. Collective decision-making over complex networks[J]. CAAI Transactions on Intelligent Systems, 2008, 3(2): 95-107. (in Chinese) [14]David Applebaum. Lévy Processes and Stochastic Calculus[M]. Cambridge: Cambridge University Press, 2009. [15]Alòs E, León J A, Vives J. On the short-time behavior of the implied volatility for jump-diffusion models with stochastic volatility[J]. Finance and Stochastics, 2007, 11(4): 571-589. [16]杜晓君, 马大明, 张 吉. 基于进化博弈的专利联盟形成研究[J]. 管理科学, 2010, 23(2): 38-44. Du Xiaojun, Ma Daming, Zhang Ji. Research on patent pool coalition based on evolutionary geme[J]. Journal of Management Science, 2010, 23(2): 38-44. (in Chinese) [17]闫 安, 达庆利, 裴 凤. 多个企业同时博弈的动态古诺模型的长期产量解研究[J]. 管理工程学报, 2013, 27(1): 94-98. Yan An, Da Qingli, Pei Feng. A study on the long-term produce solutions of dynamical model with multi-firms simultaneous-move game[J]. Journal of Industrial Engineering/Engineering Management, 2013, 27(1): 94-98. (in Chinese) [18]Szikora P. Introduction into the literature of cooperative game theory with special emphasis on dynamic games and the core[J]. Proceedings-11th International Conference on Mangement, Enterprise and Benchmarking (MEB 2013), 2013. [19]Yan Wu, Jin Yaochu, Liu Xiaoxiong. A directed search strategy for evolutionary dynamic multiobjective optimization[J]. Methodologies And Application, 2015, 19(11): 3221-3235. [20]Javier Martínez-de-Albéniz F, Rafels C. Cooperative assignment gameswith the inverse Monge property[J]. Discrete Applied Mathematics, 2014: 162(1): 42-50. [21]Friesz T L. Dynamic optimization and differential games[M]. New York: Springer, 2010. [22]陈光亚. 优化与均衡的等价性[J]. 系统科学与数学, 2009, 29(11): 1441-1446. Chen Guangya. Equivalency between optima and equilibria[J]. Journal of Systems Science & Mathematical Sciences, 2009, 29(11): 1441-1446. (in Chinese) [23]朱 亮, 韩定定. 动态复杂网络的同步拓扑演化[J]. 计算机应用, 2012, 32(2): 330-334, 339. Zhu Liang, Han Dingding. Topological evolution on synchronization of dynamic complex networks[J]. Journal of Computer Applications, 2012, 32(2): 330-334, 339. (in Chinese) [24]Bollobás B. Percolation, Connectivity, Converge and Coloring[M]. In: BélaBollobás, Robert Kozma, PezsóMiklás. Handbook of Large-Scale Random Networks, Hungary: Springer, 2008: 117-142. [25]Bollobás B, Riordan O. Random graphs and branching process[M]. In: BélaBollobás, Robert Kozma, PezsóMiklás. Handbook of Large-Scale Random Networks. Hungary: Springer, 2008: 15-116. [26]魏立峰, 陈 丽. 一类带松弛控制的Hamilton-Jacobi-Bellman方程的粘性解[J]. 山东大学学报(理学版), 2009, 44(12): 1-5. Wei Lifeng, Chen Li. Viscosity solutions of Hamilton-Jacobi-Bellman for the relaxed control[J]. Journal of Shandong University (Natural Science), 2009, 44(12): 1-5.(in Chinese) [27]Cen Liqun, Dai Weixing, Hu Shigeng. Attraction and stability for neutral stochastic functional differential equations[J]. Wuhan University Journal of Natural Science, 2009, 14(3): 205-209. [28]Samothrakis S, Lucas S, Runarsson T P, et al. Coevolving game-playing agents: Measuring performance and intransitivities[J]. Evolutionary Computation, IEEE Transactions on, 2013, 17(2): 213-226. [29]郭 英. 随机Volterra积分方程相容解的稳定性[J]. 应用数学学报, 2011, 3(2): 331-340. Guo Ying. Stability of adapted solutions of stochastic volterraintegro-equations[J]. Acta Athematicae Applicatae Sinica, 2011, 3(2): 331-340. (in Chinese) Optimal strategies of agents in deterministic multi-local-worlds graph ZHENGZhan1,ZHENGXiao-jing2*,XUXu-song3 1. Wuhan Textile University, Wuhan 430073, China; 2. Harbin University of Commerce, Harbin 150076, China; 3. Wuhan University, Wuhan 430072, China In a short time-scale, the optimal strategy of Agent for complex management systems is determined by using the analytic method in a deterministic system topology structure. A game model in the deterministic multi-local-worlds graph is constructed and the equilibrium solutions of Agents behavior are discussed for deterministic Multi-Local-Worlds graphs in two cases, which are the cooperative game between agents in the same local-world and non-cooperative game between agents in different Local-Worlds; The two different solutions with corresponding game models are coupled together to get the optimal strategies of Agents and the stability of the optimal strategy is discussed at the end of paper. deterministic; multi-local-worlds graph; optimal strategies of agents; stochastic differential game 2014-08-12; 2015-10-28. 国家自然科学基金资助项目(71503188; 71040001; 70771083). 郑小京(1975—), 男, 陕西白水人, 博士, 副教授. Email: tkwiloi_75@126.com F273.6 A 1007-9807(2016)01-0035-125 最优策略的稳定性
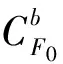


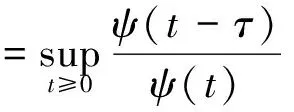
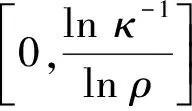


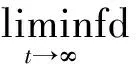

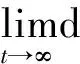

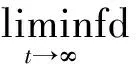


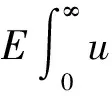

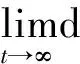

6 结束语

