EDELSTEIN-SUZUKI-TYPE RESULTS FOR SELF-MAPPINGS IN VARIOUS ABSTRACT SPACES WITH APPLICATION TO FUNCTIONAL EQUATIONS∗

Stojan RADENOVIĆFaculty of Mathematics and Information Technology Teacher Education,Dong Thap University,CaoLanh City,Dong Thap Province,Viet NamE-mail:fixedpoint@gmail.comPeyman SALIMIYoung Researchers and Elite Club,Rasht Branch,Islamic Azad University,Rasht,IranE-mail:salimipeyman@gmailCalogero VETROUniversità degli Studi di Palermo,Dipartimento di Matematica e Informatica,Via Archira fi,34,90123 Palermo,ItalyE-mail:cvetro@math.unipa.itTatjana DOŠENOVIĆFaculty of Technology,University of Novi Sad,SerbiaE-mail:tatjanad@tf.uns.ac.rs



EDELSTEIN-SUZUKI-TYPE RESULTS FOR SELF-MAPPINGS IN VARIOUS ABSTRACT SPACES WITH APPLICATION TO FUNCTIONAL EQUATIONS∗

Stojan RADENOVIĆ
Faculty of Mathematics and Information Technology Teacher Education,Dong Thap University,CaoLanh City,Dong Thap Province,Viet Nam
E-mail:fixedpoint@gmail.com
Peyman SALIMI
Young Researchers and Elite Club,Rasht Branch,Islamic Azad University,Rasht,Iran
E-mail:salimipeyman@gmail
Calogero VETRO
Università degli Studi di Palermo,Dipartimento di Matematica e Informatica,Via Archira fi,34,90123 Palermo,Italy
E-mail:cvetro@math.unipa.it
Tatjana DOŠENOVIĆ
Faculty of Technology,University of Novi Sad,Serbia
E-mail:tatjanad@tf.uns.ac.rs

AbstractThe fixed point theory provides a sound basis for studying many problems in pure and applied sciences.In this paper,we use the notions of sequential compactness and completeness to prove Eldeisten-Suzuki-type fixed point results for self-mappings in various abstract spaces.We apply our results to get a bounded solution of a functional equation arising in dynamic programming.

Key wordsG-metric space;G-cone metric space;quasi-metric space; fixed point;Edelstein’s theorem;Suzuki’s theorem.

2010 MR Subject Classi fi cation47H10;54H25;55M20

∗Received November 10,2014;revised May 14,2015.Third author was supported by Università degli Studi di Palermo,Local University Project R.S.ex 60%.Fourth author was supported by MNTRRS-174009.

1 Introduction

In view of the fact that the metric fixed point theory provides a sound basis for studying many problems in pure and applied sciences,many authors investigated the possibility of generalizing the notions of metric and metric space.Following this line of research,Dhage[14]introduced the notion of D-metric space.Later on,Mustafa and Sims[31]showed that most of the results concerning Dhage’s D-metric spaces are invalid.Thus,they introduced a new concept of generalized metric known as G-metric.After that,many researchers studied fixed point theorems in the setting of generalized metric spaces[1,3-5,7,8,11,16,18,26,28,29,31-36,38,39,44].In particular,Beg et al.[11]introduced G-cone metric spaces as a proper generalization of G-metric spaces.

On the other hand,in the development of fixed point theory and its techniques,a fundamental tool is given by contractive conditions satis fied by the involved mappings.Indeed,starting from the Banach’s contraction principle[9],the literature is rich in attempts of de fi ning weakly contractive conditions.Here,for our further use,we recall the following well-known fixed point theorems.In 1962,Edelstein[22]proved the following version of Banach’s contraction principle.

Theorem 1.1Let(X,d)be a compact metric space and let f be a self-mapping on X.Assume that d(fx,fy)＜d(x,y)for all x,y∈X with xy.Then f has a unique fixed point.

Recently,Suzuki[45]improved the results of Banach and Edelstein in the following theorem.

Theorem 1.2Let(X,d)be a compact metric space and let f be a self-mapping on X.Assume that

for all x,y∈X.Then f has a unique fixed point.

For some results,in the setting of metric or cone metric spaces,that are variants of the result of Suzuki,see[21];for other results see[23,25,37,40,41].

In this paper,we introduce the notion of Edelstein-Suzuki-G-ϕ-ψ-contraction and prove some fixed point theorems by using the hypothesis of sequential compactness of the given G-metric space.In this way,we generalize the theorems of Edelstein and Suzuki.Moreover,we extend our results to G-cone metric spaces.Finally,we present some results in the setting of G-complete G-metric spaces to obtain a bounded solution of a functional equation arising in dynamic programming.

2 Preliminaries

Here,we give preliminaries and basic de finitions which will be helpful in the sequel.First,we recall the concepts of G-metric and G-metric space.

De finition 2.1(see[31])Let X be a nonempty set and G:X3→[0,+∞)be a function satisfying the following properties:

(G1)G(x,y,z)=0 if x=y=z;

(G2)0＜G(x,x,y),for all x,y∈X with xy;

(G3)G(x,x,y)≤G(x,y,z)for all x,y,z∈X with zy;

(G4)G(x,y,z)=G(x,z,y)=G(y,z,x)=···(symmetry in all three variables);

(G5)G(x,y,z)≤G(x,a,a)+G(a,y,z)for all x,y,z,a∈X(rectangle inequality).

Then the function G is called a generalized metric or,more speci fi cally,a G-metric on X and the pair(X,G)is called a G-metric space.

De finition 2.2(see[31])Let(X,G)be a G-metric space and let{xn}be a sequence of points of X.A point x∈X is said to be the limit of the sequence{xn}if0,and we say that the sequence{xn}is G-convergent to x or that{xn}G-converges to x.

Thus,xn→x in a G-metric space(X,G)if for any ε＞0 there exists k∈N such that G(x,xn,xm)＜ε for all m,n≥k.

Proposition 2.3(see[31])Let(X,G)be a G-metric space.Then the following are equivalent:

1.{xn}is G-convergent to x;

2.G(xn,xn,x)→0 as n→+∞;

3.G(xn,x,x)→0 as n→+∞.

De finition 2.4(see[31])Let(X,G)be a G-metric space.A sequence{xn}in X is called G-Cauchy if for every ε＞0 there is k∈N such that G(xn,xm,xl)＜ε for all n,m,l≥k,that is,G(xn,xm,xl)→0 as n,m,l→+∞.

Proposition 2.5(see[31])Let(X,G)be a G-metric space.Then the following are equivalent:

1.the sequence{xn}is G-Cauchy;

2.for every ε＞0,there is k∈N such that G(xn,xm,xm)＜ε for all n,m≥k.

De finition 2.6(see[31])A G-metric space(X,G)is called G-complete if every G-Cauchy sequence in(X,G)is G-convergent in(X,G).

Proposition 2.7(see[31])Let(X,G)be a G-metric space.The function G(x,y,z)is jointly continuous in all three of its variables.

Proposition 2.8(see[31])Let(X,G)be a G-metric space.Then,for any x,y,z,a∈X it follows that:

(i)If G(x,y,z)=0,then x=y=z;

(ii)G(x,y,z)≤G(x,x,y)+G(x,x,z);

(iii)G(x,y,y)≤2G(y,x,x);

(iv)G(x,y,z)≤G(x,a,z)+G(a,y,z);

(vi)G(x,y,z)≤G(x,a,a)+G(y,a,a)+G(z,a,a).

Note that any G-metric space(X,G)induces a metric dGon X given by

Moreover,(X,G)is G-complete if and only if(X,dG)is complete.

Lemma 2.9(see[30])Let(X,G)be a G-metric space and x1,x2,y1,y2,z1,z2,a∈X where x1x2,y1y2and z1z2.Then the following inequality holds:

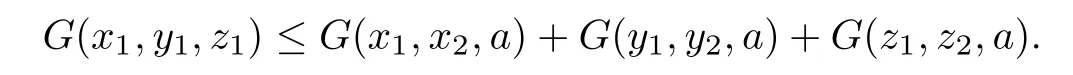
De finition 2.10(see[30])Let(X,G)be a G-metric space and A be a nonempty subset of X.The subset A is called sequentially G-compact if for any sequence{xn}in A there exists a subsequence xnkof{xn}which G-converges to some x∈A.

We recall also some de finitions concerned with quasi-metric spaces that can be found in[27,42]and the references therein.

De finition 2.11Let X be a nonempty set and d:X2→[0,+∞)be a function.Assume that the following assertions hold:

(i)d(x,y)=0 i ff x=y;

(ii)d(x,y)≤d(x,z)+d(z,y)for all x,y,z∈X.

Then(X,d)is called a quasi-metric space.

De finition 2.12Let(X,d)be a quasi-metric space,{xn}be a sequence in X and x∈X.The sequence{xn}converges to x if

De finition 2.13Let(X,d)be a quasi-metric space and{xn}be a sequence in X.We say that:

1.{xn}is left-Cauchy if for every∈＞0 there exists a positive integer N=N(∈)such that d(xn,xm)＜∈for all n＞m＞N;

2.{xn}is right-Cauchy if for every∈＞0 there exists a positive integer N=N(∈)such that d(xn,xm)＜∈for all m＞n＞N;

3.{xn}is Cauchy if for every∈＞0 there exists a positive integer N=N(∈)such that d(xn,xm)＜∈for all m,n＞N.

De finition 2.14Let(X,d)be a quasi-metric space.Then

1.(X,d)is left-complete if each left-Cauchy sequence in X is convergent;

2.(X,d)is right-complete if each right-Cauchy sequence in X is convergent;

3.(X,d)is complete if each Cauchy sequence in X is convergent.

Theorem 2.15(see[27])Let(X,G)be a G-metric space.Let d:X2→[0,+∞)be the function de fined by d(x,y)=G(x,y,y).Then

•(X,d)is a quasi-metric space;

•{xn}⊆X G-converges to x∈X if and only if{xn}converges to x∈X in(X,d);

•{xn}is G-Cauchy if and only if{xn}is Cauchy in(X,d);

•(X,G)is G-complete if and only if(X,d)is complete.

De finition 2.16A function ψ:[0,+∞)3→[0,+∞)is called jointly upper semi-continuous in all three of its variables when for all sequences{xm},{yn}and{zl}such that

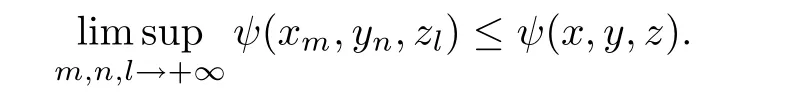
De finition 2.17Let(X,G)be a G-metric space,ϕ:[0,+∞)→[0,+∞)be a function such thatfor all t≥0 and ψ:[0,+∞)3→[0,+∞)be a function which is jointly upper semi-continuous in all three of its variables.A mapping f:X→X is called an Edelstein-Suzuki-G-ϕ-ψ-contraction if

implies

for all x,y∈X,where ψ(t,t,0)≤t for all t≥0.

3 Fixed Point Results on Sequentially G-Compact G-Metric Spaces

In this section we will prove a fixed point theorem for Edelstein-Suzuki-G-ϕ-ψ-contractions in G-metric spaces and deduce some corollaries.We note that in recent papers[27,42],it was shown that in some cases G-metric fixed point results can be obtained directly from their standard metric or quasi-metric counterparts.However,our Edelstein-Suzuki-type results for G-metric and G-cone metric spaces cannot be obtained in this way.

Theorem 3.1Let(X,G)be a sequentially G-compact G-metric space and f be an Edelstein-Suzuki-G-ϕ-ψ-contraction on X.Then f has a fixed point.Moreover,if ψ(t,0,t)≤12t for all t≥0 then f has a unique fixed point.

ProofLet λ=inf{G(x,fx,f2x):x∈X}.There exists a sequence{xn}in X such thatBy sequentially G-compactness of X,we can assume that there exist w1,w2,w3∈X such that

Hence,by the continuity of function G,we have

Now,we show that λ must be equal to 0.

If λ＞0,then there exists N∈N such that for all n≥N,we have

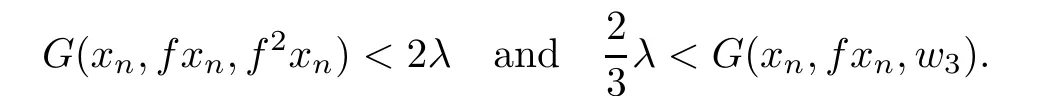
Therefore for all n≥N,we get

Now,by(2.1),we have

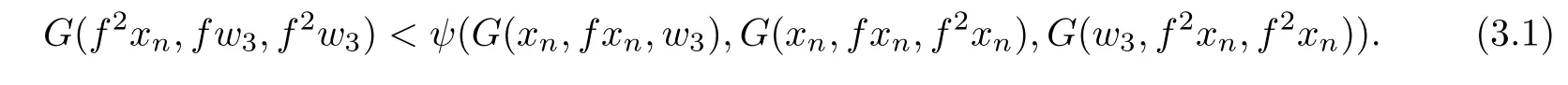
By taking the upper limit as n→+∞in(3.1),we get

and hence G(w3,fw3,f2w3)≤λ.Therefore,by the de finition of λ,we have

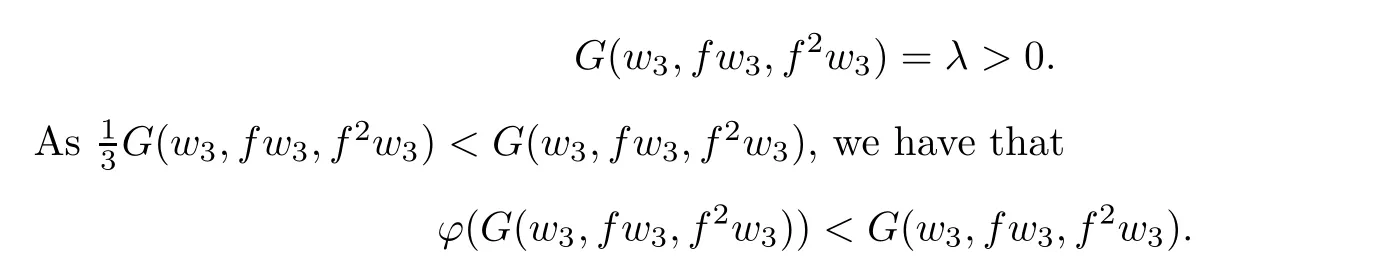
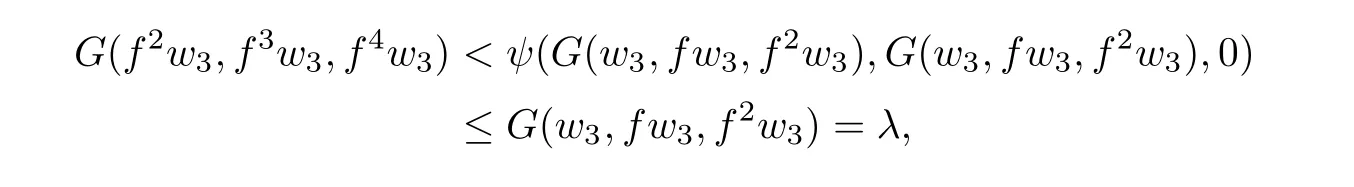
Now by(2.1)with x=w3and y=f2w3,we getwhich is a contradiction with the de finition of λ and so λ=0,that is,w1=w2=w3.

Now,we shall show that f has at least one fixed point.Assume towards a contradiction that f has no fixed points.Hence,fromwe obtain

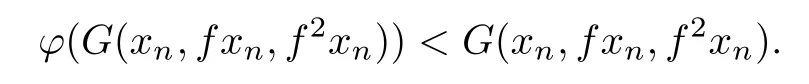
As(X,G)is sequentially G-compact,we can assume that f3xn→u and f4xn→v with u,v∈X.Now,by(2.1)with x=xnand y=f2xn,we have

By taking the upper limit as n→+∞,we get G(w1,u,v)=0 and so

Now,suppose that both of the following inequalities hold for some n∈N,

and

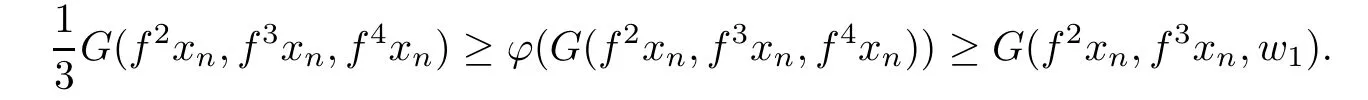
Since xnfxnand f2xnf3xn,by Lemma 2.9,we have

which is a contradiction.Thus,for each n∈N,either

or

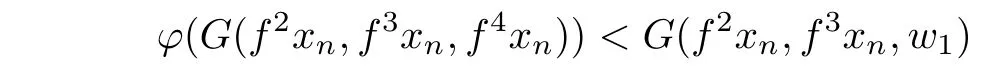
holds.Therefore,by hypotheses,we conclude that

or

holds for all n in an in finite subset of N.Taking the upper limit as n→+∞in each of these inequalities that holds for all n in an in finite subset of N,we obtain

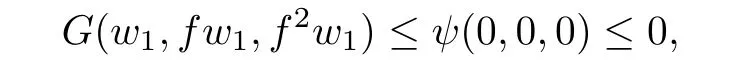
that is,w1=fw1=f2w1.We conclude that w1is a fixed point of f.

To prove the uniqueness of w1,suppose that w0is another fixed point of f such that w1w0.Hence

Now by(2.1),we have

On the other hand,by Proposition 2.8(iii)we have

Consequently,we obtain easily the contradiction G(w1,w0,w0)＜G(w1,w0,w0).Therefore w1=w0and so w1is the unique fixed point of f.

Corollary 3.2Let(X,G)be a sequentially G-compact G-metric space and f be a selfmapping on X such that

implies

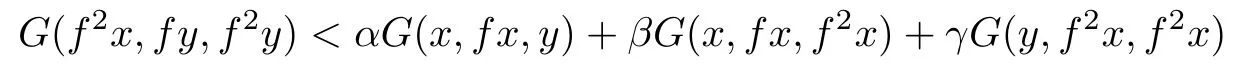
for all x,y∈X,where α,β,γ≥0 with α+β≤1.Then f has a fixed point.Moreover,ifthen f has a unique fixed point.

If in Corollary 3.2 we take α=γ=0,β=1 and k=1 we obtain the following corollary.

Corollary 3.3Let(X,G)be a sequentially G-compact G-metric space and f be a selfmapping on X such that

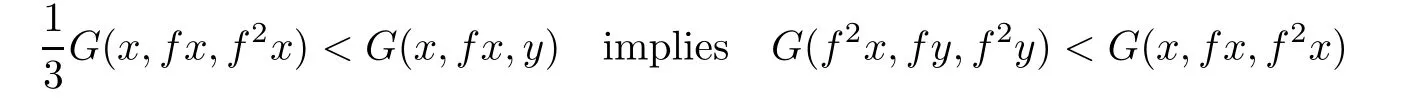
for all x,y∈X.Then f has a unique fixed point.

If in Corollary 3.2 we take β=γ=0 and k=1 we obtain the following corollary.

Corollary 3.4Let(X,G)be a sequentially G-compact G-metric space and f be a selfmapping on X such that

for all x,y∈X,where 0＜α≤1.Then f has a fixed point.Moreover,ifthen f has a unique fixed point.

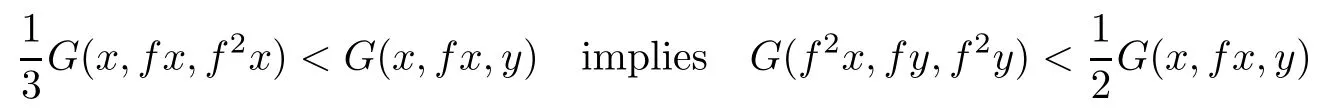
for all x,y∈X and so Corollary 3.4 is applicable to the mapping f.

Example 3.6Let X={0,1,2}and G:X3→[0,+∞)be given as

and extended by symmetry.Then it is easy to check that(X,G)is a sequentially G-compact G-metric space which is asymmetric since,e.g.,G(0,0,2)G(0,2,2).De fi ne f:X→X by f0=f1=0 and f2=1.Then f satisfies the condition of Corollary 3.1 with(for instance)and so f has a unique fixed point.

4 Fixed Point Results on G-Cone Metric Spaces

In this section,we extend our results to G-cone metric spaces.To this aim,we recall the following concepts.

Let(E,‖·‖)be a real Banach space with θ as the zero element.A subset P of E is called a cone if and only if the following conditions are satis fied

(i)P is closed,nonempty and P{θ};

(ii)a,b≥0 and x∈P imply ax+by∈P;

(iii)x∈P and−x∈P imply x=θ.

For the given cone P⊂E,we de fi ne a partial ordering≾on E with respect to P by x≾y if and only if y−x∈P;we write x≺y whenever x≾y and xy,while x≪y will stand for y−x∈intP(the interior of P).The cone P⊂E is called normal if there is a positive real number K such that for all x,y∈E,θ≾x≾y⇒‖x‖≤K‖y‖.The least positive number satisfying the above inequality is called the normal constant of P.If K=1 then the cone P is called monotone.For instance,if E=R2,P={(x,y):x≥0,y≥0},then P is a such cone.

Lemma 4.1(see[23])Let(E,‖·‖)be a real Banach space with a monotone solid cone P.Then,for all x,y∈E,

De finition 4.2(see[11])Let(E,‖·‖)be a real Banach space with a solid cone P and Gc:X3→E be a function satisfying the following properties:

(F1)If x=y=z,then Gc(x,y,z)=θ;

(F2)θ≪Gc(x,y,y),for any x,y∈X with xy;

(F3)Gc(x,x,y)≾Gc(x,y,z)for any x,y,z∈X,with yz;

(F4)Gc(x,y,z)=Gc(x,z,y)=Gc(y,z,x)=···(symmetry in all three variables);

(F5)Gc(x,y,z)≾Gc(x,a,a)+Gc(a,y,z)for all x,y,z,a∈X(rectangle inequality).Then Gcis called a G-cone metric on X and the pair(X,Gc)is called a G-cone metric space.

Proposition 4.3(see[30])Let(E,‖·‖)be a real Banach space with a monotone solid cone P.If Gc:X3→E is a G-cone metric on X,then the function G:X3→[0,+∞)de fined by G(x,y,z)=‖Gc(x,y,z)‖is a G-metric on X and(X,G)is a G-metric space.

For more details on cone metric spaces and related results,we refer the reader to[2,6,15,17,19,20,46-48].

Now,we are ready to state and prove the following theorem.

Theorem 4.4Let(E,‖·‖)be a real Banach space with a monotone solid cone P and(X,Gc)be a G-cone metric space.Assume that(X,‖Gc‖)is a sequentially G-compact G-metric space and f:X→X is such that

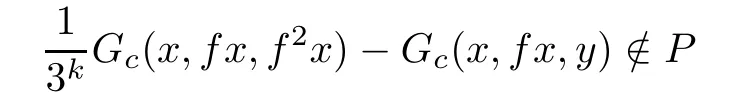
implies

for all x,y∈X,where α,β,γ≥0 with 0＜α+β≤1.Then f has a fixed point.Moreover,ifthen f has a unique fixed point.

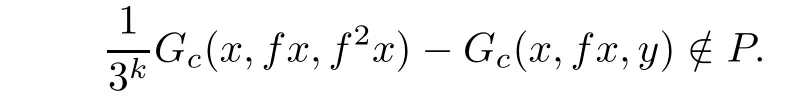
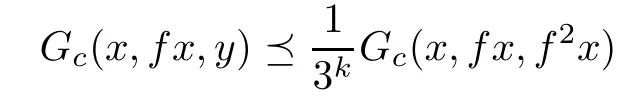
Thus,we can apply Corollary 3.2 to deduce that f has a fixed point.Furthermore,ifthen f has a unique fixed point.

If in Theorem 4.4 we take α=γ=0,β=1 and k=1 we obtain the following corollary.

Corollary 4.5Let(E,‖·‖)be a real Banach space with a monotone solid cone P and(X,Gc)be a G-cone metric space.Assume that(X,‖Gc‖)is a sequentially G-compact G-metric space and f:X→X is such that

for all x,y∈X.Then f has a unique fixed point.

If in Theorem 4.4 we take β=γ=0 and k=1 we obtain the following corollary.

Corollary 4.6Let(E,‖·‖)be a real Banach space with a monotone solid cone P and(X,Gc)be a G-cone metric space.Assume that(X,‖Gc‖)is a sequentially G-compact G-metric space and f:X→X is such that

for all x,y∈X where 0＜α≤1.Then f has a fixed point.Moreover,ifthen f has a unique fixed point.

Example 4.7Let X={a,b},E=R3,P={(x,y,z)∈E:x,y,z≥0}.De fi ne G:X3→E by

Then(X,G)is an asymmetric G-cone metric space as G(a,a,b)G(a,b,b).Further let f:X→X with fa=fb=a.It is not hard to see that f satisfies the conditions of Corollary 4.2.

5 Fixed Point Results on G-Metric Spaces via Quasi-Metric Spaces

In this section,we first of all present some fixed point results in the setting of quasi-metric spaces by using the following concept and then deduce some corollaries in the setting of G-metric spaces.

De finition 5.1(see[43])Let f be a self-mapping on X and α:X×X→[0,+∞)be a function.We say that f is an α-admissible mapping if

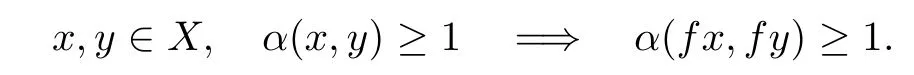
Theorem 5.2Let(X,d)be a complete quasi-metric space,f be a continuous α-admissible mapping on X and let there exists x0∈X such that α(x0,fx0)≥1.Assume that

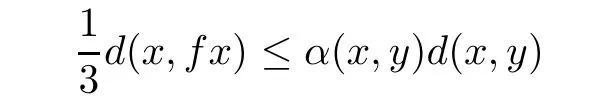
implies

for all x,y∈X,where 0≤r＜1.Then f has a fixed point.

ProofLet x0be the given point and de fi ne a sequence{xn}by xn=fnx0for all n∈N.Since f is an α-admissible mapping and α(x0,fx0)=α(x0,x1)≥1,we deduce that α(x1,x2)= α(fx0,fx1)≥1.By continuing this process,we get α(xn,xn+1)≥1 for all n∈N∪{0}.Since

then from(5.1)we have

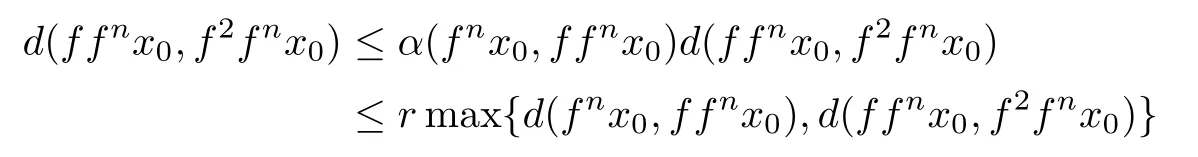
which implies

Now by(5.2),we can obtain

Then,for any m＞n,by(5.3),we get

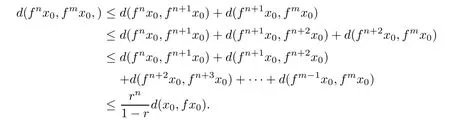
From the continuity of f we have

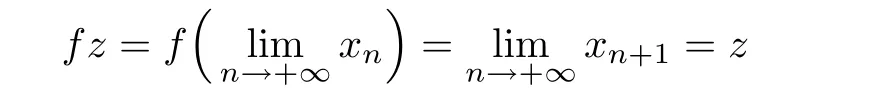
and hence z is fixed point of f.

In the following theorem,we omit the continuity of the mapping f.

Theorem 5.3Let(X,d)be a complete quasi-metric space and f be an α-admissible mapping on X such that

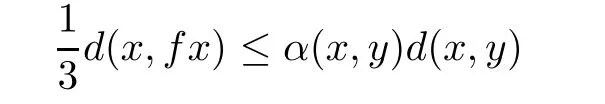
implies

for all x,y∈X,where 0≤r＜1.Assume that the following conditions hold:

(i)there exists x0∈X such that α(x0,fx0)≥1;

(ii)if{xn}is a sequence in X such that α(xn,xn+1)≥1 for all n and xn→z as n→+∞,then α(xn,z)≥1 for all n∈N∪{0}.

Then f has a fixed point.

ProofLet x0∈X be such that α(x0,fx0)≥1 and de fi ne a sequence{xn}in X by xn= fnx0=fxn−1for all n∈N.Following the proof of Theorem 5.2,we see that α(xn,xn+1)≥1 for all n∈N∪{0}and there exists z∈X such that xn→z as n→+∞.Hence,from(ii)we deduce that α(xn,z)≥1 for all n∈N∪{0}.

Now,we suppose that there exists n0∈N such that the following inequalities hold

Then,by(5.2),we have

which is a contradiction.Thus,for each n∈N,either

or

holds for every n∈N.Hence,by(5.4),it follows that one of the following inequalities holds for all n in an in finite subset of N,

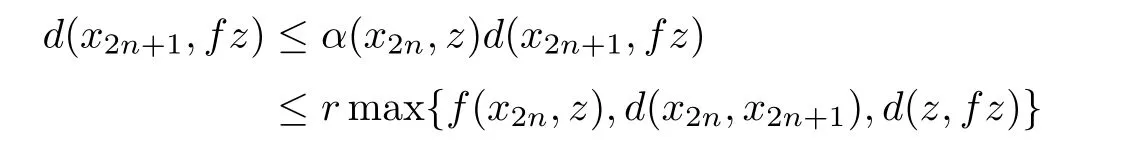
or

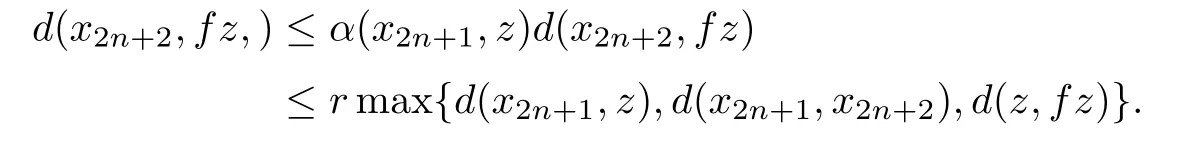
Taking the limit as n→+∞in each of these inequalities that holds for all n in an in finite subset of N,we obtain(1−r)d(z,fz)≤0 which implies z=fz.

As immediate consequences of Theorems 5.2 and 5.3,we give the following corollaries in the setting of G-metric spaces.

Corollary 5.4Let(X,G)be a G-complete G-metric space.Assume that f is a continuous α-admissible mapping on X and there exists x0∈X such that α(x0,fx0)≥1.Also,suppose that

for all x,y∈X,where 0≤r＜1.Then f has a fixed point.

Corollary 5.5Let(X,G)be a G-complete G-metric space.Assume that f is an αadmissible mapping on X such that

for all x,y∈X,where 0≤r＜1.Assume that the following conditions hold:

(i)there exists x0∈X such that α(x0,fx0)≥1;

(ii)if{xn}is a sequence in X such that α(xn,xn+1)≥1 for all n and xn→x as n→+∞,then α(xn,x)≥1 for all n∈N∪{0}.

Then f has a fixed point.

Example 5.6Let X=[0,+∞)and G(x,y,z)=|x−y|+|y−z|+|x−z|be a G-metric on X.De fi ne f:X→X by

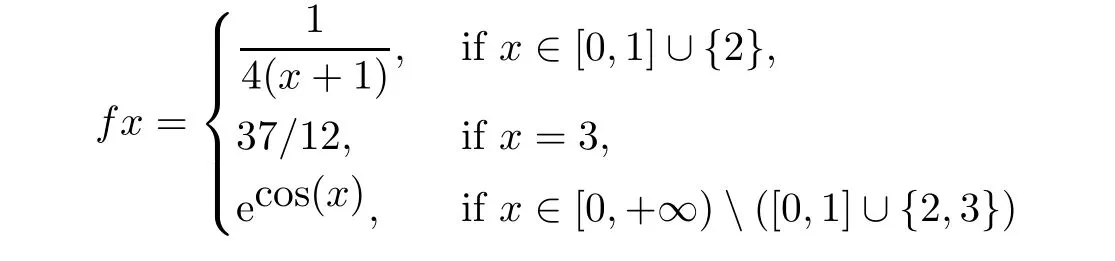
and α:X×X→[0,+∞)by

We will prove that all the hypotheses of Corollary 5.5 are satis fied and hence f has a fixed point.

Let x,y∈X.If α(x,y)≥1 then x,y∈[0,1].On the other hand for all x∈[0,1],we have fx≤1 and hence α(fx,fy)≥1.This implies that f is an α-admissible mapping on X.Obviously,α(0,f0)≥1.

Now,if{xn}is a sequence in X such that α(xn,xn+1)≥1 for all n∈N∪{0}and xn→x as n→+∞,then{xn}⊆[0,1]and hence x∈[0,1].This implies that α(xn,x)≥1 for all n∈N∪{0}.

Finally,to check condition(5.6),we distinguish the following cases:

(a)If x,y∈[0,1],then

(b)If x=2 and y=3,then

but

(c)Otherwise,condition(5.6)trivially holds.

We conclude that

Thus,all the conditions of Corollary 5.5 are satis fied and hence f has a fixed point.

The next theorem gives su ffi cient conditions to obtain the uniqueness of the fixed point.

Theorem 5.7Assume that all the hypotheses of Corollary 5.4(respectively,Corollary 5.5)hold.Adding the following condition:

ProofSuppose that z and z∗are two fixed points of f such that zz∗.By condition(iii),there exists v such that α(z,v)≥1 and α(z∗,v)≥1.Therefore,we have

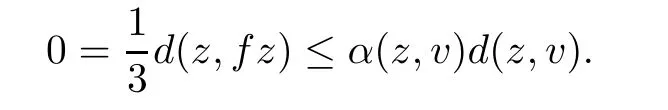
It follows,by(5.5),that

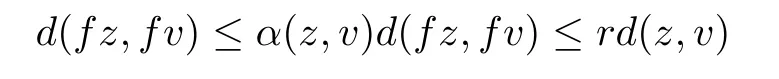
and hence we can deduce easily that

By taking the limit as n→+∞in the above inequality we obtain fnv→z.Similarly,we get fnv→z∗as n→+∞and so z=z∗.

Corollary 5.8Let(X,G)be a G-complete G-metric space and f be an α-admissible mapping,such that

for all x,y∈X where 0≤r＜1.Assume that the following conditions hold

(i)there exists x0∈X such that α(x0,fx0)≥1;

(ii)if{xn}is a sequence in X such that α(xn,xn+1)≥1 for all n and xn→x as n→+∞,then α(xn,x)≥1 for all n∈N∪{0}.

Then f has a fixed point.Further,if for all x,y∈X with xy there exists v∈X such that α(x,v)≥1 and α(y,v)≥1,we obtain the uniqueness of the fixed point.

6 Application to Functional Equations

In this section,we show how it is possible to study the existence and uniqueness of the bounded solution of a functional equation by using Corollary 5.8.Here we assume that U and V are Banach spaces,W⊆U is a state space and D⊆V is a decision space.

It is well known that the dynamic programming provides useful tools for mathematical optimization and computer programming as well,see[10,12,13].In particular,the problem of dynamic programming related to multistage process reduces to the problem of solving the functional equation

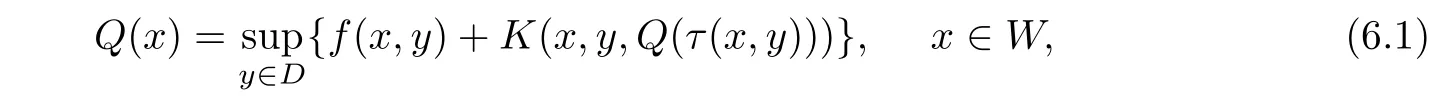
where τ:W×D→W,f:W×D→R,K:W×D×R→R.

Let B(W)denote the space of all bounded real-valued functions on W.Clearly,this space endowed with the G-metric given by

is a G-complete G-metric space.We will prove the following theorem.

Theorem 6.1Let K:W×D×R→R and f:W×D→R be two bounded functions and let A:B(W)→B(W)be de fined by

for all h∈B(W)and x∈W.Assume that the following condition holds:

where x∈W and y∈D.Then the functional equation(6.1)has a unique bounded solution.

ProofNote that(B(W),G)is a G-complete G-metric space.Let ε be an arbitrary positive number,x∈W and h1,h2∈B(W),then there exist y1,y2∈D such that

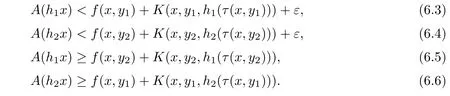
Then from(6.3)and(6.6),it follows easily that

Hence we get

Similarly,from(6.4)and(6.5)we obtain

Therefore,from(6.7)and(6.8)we have

that implies,

Since the above inequality is true for any x∈W and ε＞0 is taken arbitrary,then we conclude immediately that

Thus all the hypotheses of Corollary 5.8 are satis fied,with α(x,y)=1 for all x,y∈X and r=1/2.We conclude that the operator A,given by(6.2),has a unique fixed point,and hence the functional equation(6.1)has a unique bounded solution.

References

[1]Abbas M,Nazir T,Vetro P.Common fixed point results for three maps in G-metric spaces.Filomat,2011,25:1-17

[2]Abbas M,Vetro P,Khan S H.On fixed points of Berinde’s contractive mappings in cone metric spaces.Carpathian J Math,2010,26:121-133

[3]Abbas M,Nazir T,Radenović S.Some periodic point results in generalized metric space.Appl Math Comput,2010,217:4094-4099

[4]Abbas M,Nazir T,Radenović S.Common fixed point of generalized weakly contractive maps in partially ordered G-metric spaces.Appl Math Comput,2012,218(18):9383-9395

[5]Agarwal R P,Kadelburg Z,Radenović S.On coupled fixed point results in asymmetric G-metric spaces.J Ineq Appl,2013,2013:528

[6]Arshad M,Azam A,Vetro P.Some common fixed point results in cone metric spaces.Fixed Point Theory Appl,2009,2009:Article ID 493965

[7]Aydi H,Shatanawi W,Vetro C.On generalized weakly G-contraction mapping in G-metric spaces.Comput Math Appl,2011,62:4222-4229

[8]Aydi H,Chauhan S,Radenović S.Fixed points of weakly compatible mappings in G-metric spaces satisfying common limit range property.Facta Universitatis,Ser Math Inf,2013,28(2):197-210

[9]Banach S.Sur les opérations dans les ensembles abstraits et leur application auxéquations intégrales.Fund Math,1922,3:133-181

[10]Baskaran R,Subrahmanyam P V.A note on the solution of a class of functional equations.Appl Anal,1986,22:235-241

[11]Beg I,Abbas M,Nazir T.Generalized cone metric spaces.J Nonlinear Sci Appl,2010,1:21-31

[12]Bellman R.Methods of Nonlinear Analysis,Vol II.New York:Academic Press,1973

[13]Bellman R,Lee E S.Functional equations in dynamic programming.Aequationes Math,1978,17:1-18

[14]Dhage B C.Generalized metric space and mappings with fixed point.Bull Calcutta Math Soc,1992,84:329-336

[15]Di Bari C,Saadati R,Vetro P.Common fixed points in cone metric spaces for CJM-pairs.Math Comput Modelling,2011,54:2348-2354

[16]Di Bari C,Vetro C.Common fixed point theorems for weakly compatible maps satisfying a general contractive condition.Int J Math Math Sci,2008,2008:Article ID 891375

[17]Di Bari C,Vetro P.Common fixed points in cone metric spaces for MK-pairs and L-pairs.Ars Combin,2011,99:429-437

[18]Di Bari C,Vetro P.Common fixed points in generalized metric spaces.Appl Math Comput,2012,218:7322-7325

[19]Di Bari C,Vetro P.ϕ-pairs and common fixed points in cone metric spaces.Rend Circ Mat Palermo,2008,57:279-285

[20]Di Bari C,Vetro P.Weakly ϕ-pairs and common fixed points in cone metric spaces.Rend Circ Mat Palermo,2009,58:125-132

[21]-Dorić D,Kadelburg Z,Radenović S.Edelstein-Suzuki-type fixed point results in metric and abstract metric spaces.Nonlinear Anal,2012,75:1927-1932

[22]Edelstein M.On fixed and periodic points under contractive mappings.J London Math Soc,1962,37:74-79

[23]Farajzadeh A P,Amini-Harandi A,Baleanu D.Fixed point theory for generalized contractions in cone metric space.Commun Nonlinear Sci Numer Simulat,2012,17:708-712

[24]Huang L G,Zhang X.Cone metric spaces and fixed point theorems of contractive mappings.J Math Anal Appl,2007,332:1468-1476

[25]Hussain N,-Dorić D,Kadelburg Z,Radenović S.Suzuki-type fixed point results in metric type spaces.Fixed Point Theory Appl,2012,2012:126

[26]Hussain N,Karapinar E,Salimi P,Vetro P.Fixed point results for Gm-Meir-Keeler contractive and G-(α,ψ)-Meir-Keeler contractive mappings.Fixed Point Theory Appl,2013,2013:34

[27]Jleli M,Samet B.Remarks on G-metric spaces and fixed point theorems.Fixed Point Theory Appl,2012,2012:210

[28]Kadelburg Z,Nashine H K,Radenović S.Common coupled fixed point results in partially ordered G-metric space.Bull Math Anal Appl,2012,4(2):51-63

[29]Long W,Abbas M,Nazir T,Radenović S.Common fixed point for two pairs of mappings satisfying(E,A)-property in generalized metric spaces.Abstarct Appl Anal,2012,2012:Article ID 394830

[30]Moradlou F,Salimi P,Vetro P.Some new extensions of Edelstein-Suzuki-type fixed point theorem to G-metric and G-cone metric spaces.Acta Math Sci,2013,33B(4):1049-1058

[31]Mustafa Z,Sims B.A new approach to generalized metric spaces.J Nonlinear Convex Anal,2006,7:289-297

[32]Mustafa Z,Sims B.Some remarks concerning D-metric spaces.Proc Int Conf on Fixed Point Theory and Applications,Valencia(Spain),July(2003),189-198

[33]Mustafa Z,Shatanawi W,Bataineh M.Existence of fixed point results in G-metric spaces.Int J Math Math Sci,2009,2009:Article ID 283028

[34]Mustafa Z,Obiedat H,Awawdeh F.Some common fixed point theorem for mapping on complete G-metricspaces.Fixed Point Theory Appl,2008,2008:Article ID 189870

[35]Nashine H K,Kadelburg Z,Radenović S.Coincidence and fixed point results under generalized weakly contractive condition in partially ordered G-metric spaces.Filomat,2013,27(7):1333-1343

[36]Nashine H K,Kadelburg Z,Pathak R P,Radenović S.Coincidence and fixed point results in ordered G-cone metric spaces.Math Comput Model,2013,57:701-709

[37]Paesano D,Vetro P.Suzuki’s type characterizations of completeness for partial metric spaces and fixed points for partially ordered metric spaces.Topology Appl,2012,159:911-920

[38]Radenović S.Remarks on some recent coupled coincidence point results in symmetric G-metric spaces.J Operators,2013,2013:Article ID 290525

[39]Radenović S,Pantelić S,Salimi P,Vujaković J.A note on some tripled coincidence point results in G-metric spaces.Int J Math Sci Eng Appl,2012,6(6):23-38

[40]Saadati R,Vaezpour S M,Vetro P,Rhoades B E.Fixed point theorems in generalized partially ordered G-metric spaces.Math Comput Modelling,2010,52:797-801

[41]Salimi P,Karapinar E.Suzuki-Edelstein type contractions via auxiliary functions.Math Problems Eng,2013,2013:Article ID 648528

[42]Samet B,Vetro C,Vetro F.Remarks on G-metric spaces.Int J Analysis,2013,2013:Article ID 917158

[43]Samet B,Vetro C,Vetro P.Fixed point theorems for α-ψ-contractive type mappings.Nonlinear Anal,2012,75:2154-2165

[44]Shatanawi W.Fixed point theory for contractive mappings satisfying Φ-maps in G-metric spaces.Fixed Point Theory Appl,2010,2010:Article ID 181650

[45]Suzuki T.A new type of fixed point theorem in metric spaces.Nonlinear Anal,2009,71:5313-5317

[46]Vetro P.Common fixed points in cone metric spaces.Rend Circ Mat Palermo,2007,56:464-468

[47]Vetro P,Akbar A A,Arshad M.Fixed point results in cone metric spaces for contractions of Zam firescu type.Indian J Math,2010,52:251-261

[48]Vetro P,Akbar A A,Arshad M.Fixed point results in cone metric spaces.Int J Mod Math,2010,5:101-108