NONSMOOTH CRITICAL POINT THEOREMS AND ITS APPLICATIONS TO QUASILINEAR SCHRÖDINGER EQUATIONS∗
Zhouxin LI(李周欣)School of Mathematics and Statistics,Central South University,Changsha 400083,ChinaE-mail:lzx@math.pku.edu.cnYaotian SHEN(沈尧天)Department of Mathematics,South China University of Technology,Guangzhou 510640,ChinaE-mail:maytshen@scut.edu.cn
NONSMOOTH CRITICAL POINT THEOREMS AND ITS APPLICATIONS TO QUASILINEAR SCHRÖDINGER EQUATIONS∗
Zhouxin LI(李周欣)
School of Mathematics and Statistics,Central South University,Changsha 400083,China
E-mail:lzx@math.pku.edu.cn
Yaotian SHEN(沈尧天)
Department of Mathematics,South China University of Technology,Guangzhou 510640,China
E-mail:maytshen@scut.edu.cn
AbstractIn this paper,the existence and nonexistence of solutions to a class of quasilinear elliptic equations with nonsmooth functionals are discussed,and the results obtained are applied to quasilinear Schrödinger equations with negative parameter which arose from the study of self-channeling of high-power ultrashort laser in matter.
Key wordsnonsmooth critical point theorems;quasilinear elliptic equations;Schrödinger equation
2010 MR Subject Classi fi cation35J20;35J65;35J10
∗Received December 5,2014;revised May 13,2015.The first author was supported by NSF of China(11201488)and Hunan Provincial Natural Science Foundation of China(14JJ4002).The second author was supported by NSF of China(11371146).
1 Introduction and Main Results
In this paper,we consider the existence of nontrivial solutions for the following class of quasilinear elliptic equations with natural growth

where N≥3,q>2,c(x)∈C1(RN),aij(x,s)are Carathéodory functions,∂saijdenotes the derivatives of aijwith respect to s.The repeated indices indicate the summation from 1 to N.
As an example,in this paper,we also consider a special case of equation(1.1).In the study of self-channeling of high-power ultrashort laser in matter[1],the following quasilinear Schrödinger equation was considered

where W(x)is a given potential,κ is a real constant.Let h(s)=(1+s)1/2and l(s)=s(q−2)/2.If we consider the standing waves of(1.2)of the form z(x,t)=exp(−iEt)u(x),we observe thatz(x,t)satisfies(1.2)if and only if u(x)solves the following equation
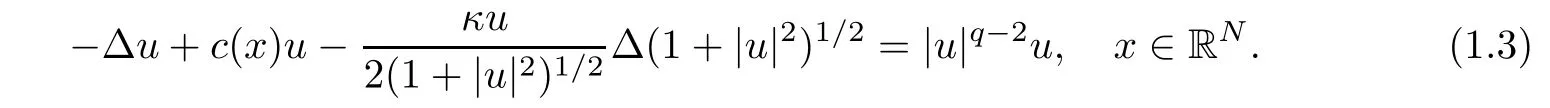
Equation(1.3)is a special case of(1.1)with
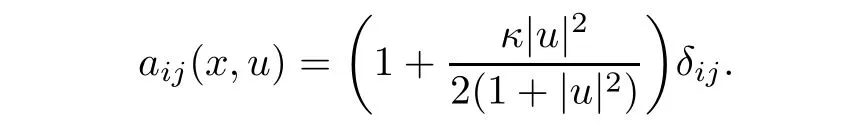
We make the following assumptions on aij(x,s).
(a1)aij≡aji,and aij,∂saij∈L∝(RN×R,R);
(a2)there exist β≥α>0 such that for(x,s,ξ)∈(RN×R×RN),

(a3)there existµ∈(0,1),ν∈(0,q−2)such that for(x,s,ξ)∈(RN×R×RN),

As to c(x),we assume that
(c)c(x)∈C(RN),c(x)≥0 for x∈RNand
We de fi ne the Hilbert space

endowed with the inner product〈u,v〉=RN(∇u∇v+c(x)uv)and with the norm
Under condition(c),the imbedding from X into Lp(RN)is continuous for 1≤p≤2∗,and is compact for 1≤p<2∗,see[2].These imbedding results hold if(c)is replaced by one of the following conditions:
(c1)ess inf c(x)>0,and for any M>0 and any r>0 there holds

where Br(y)={x∈RN:|x−y|<r}(see[3]).
(c2)c(x)∈C(RN),c(x)≥c0>0 for x∈RN,and[c(x)]−1∈L1(RN)(see[4]).
The corresponding functional of(1.1)is


In order to study the existence of solutions to(1.1),we employ the nonsmooth critical point theorem in[5-7].We say that u∈X is a weak solution to(1.1)if the weak slope(see the de finition in Section 2)of I at u is zero.
On a bounded domain Ω∈RN,(1.1)was extensively studied,one can refer to[8-15]and some references therein.Moreover,in[16-19],(1.1)is studied when the principal partaij(x,u)DiuDju is unbounded in L1(Ω).In[16,17]the existence of solutions were obtained by method of approximation,in[19]the existence of in finitely many solutions were obtained by employing nonsmooth critical point theory for lower semicontinuous functionals,and in[18]the existence of solutions were proved by using a change of variable to reformulate the corresponding functional of the equation.
On unbounded domain,the problems that the principal part of(1.1)is bounded was studied also and some existence results were obtained in[2,20-22].Recently,to find solutions of(1.1)on unbounded domain with principal part unbounded attracted increasing interest,see for examples[23,24].Gluing techniques were used in[23]for periodic problems.In[24]a new method of change of variable,which can be applied to a more general class of quasilinear elliptic problems,was introduced.In most of problems,(1.1)with unbounded principal part can be reformulated to equations with bounded principal part.
In most of the studies,the natural growth term of equation(1.1)was assumed to be nonnegative,that is,for u∈X,

This is called the sign condition of the equation.In this paper,we allow the natural growth term to be negative,see(a3).As for as we know,(a3)was first introduced in[12]to study(1.1)on bounded domain Ω when q=2,and then was extended to the case 2≤q<2∗in[13].There are many equations like(1.3)with κ<0,see also Example 4.1 in[25],that do not satisfy the sign condition.Parameter κ plays an important role in(1.3)especially when it is negative.Assumption(a3)make it possible for us to study the existence of solutions to(1.3)when κ is negative.
In this paper,we prove that
Theorem 1.1Assume that(a1)-(a3),(c)hold and q∈(2,2∗),then problem(1.1)has a nontrivial weak solution in X.
In the case that(a3)does not satis fied,that is,when
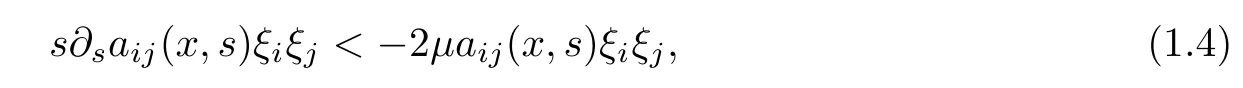
we prove that
Theorem 1.2Assume that aijare x-independent and that(a1)-(a2),(c)hold.Furthermore,assume that q∈(2,2∗),c(x)∈C1(RN),x·∇c(x)≥−(1−2q)Nc(x)and(1.4)holds.Then problem(1.1)has no nontrivial weak solution in X∩C1(RN).
Remark 1.3(i)Theorems 1.1 and 1.2 imply that−2µaij(x,s)ξiξjis the lower bound to obtain solutions for(1.1).
(ii)According to the proof of Theorem 1.2,the best constant for the lower bound is µ=1−q/2∗.
As for problem(1.3),we have
Theorem 1.4Assume that(c)holds and q∈(2,2∗),then problem(1.3)has a nontrivial weak solution in X provided that one of the following conditions holds:
(i)4≤q and 0≤κ<+∞;
(ii)2<q<4 and 0≤κ<κ∗;
(iii)−κ∗≤κ<0,
Remark 1.5(i)Part(i)in Theorem 1.4 holds only in the case N=3.Indeed,to ensure q≥4 holds,we require that 2∗>4,and this holds when N≤3.
(ii)κ∗is increasing in q∈(2,4)and κ∗→0 as q→2,κ∗→+∞as q→4.
(iii)κ∗is decreasing in q∈(2,2∗)and
Corollary 1.6Assume that(c)holds,q∈(2,2∗),κ<−κ∗and c(x)∈C1(RN),x· ∇c(x)≥−(1−2q)Nc(x),then problem(1.3)has no nontrivial solution in X∩C1(RN).
Corollary 1.7Assume that(c)holds,q=2∗,κ<0 and c(x)∈C1(RN),x·∇c(x)>−2c(x),then problem(1.3)has no nontrivial solution in X∩C1(RN).
This paper is organized as the following.In Section 2,we present the nonsmooth variational framework and analyse the compactness of(PS)sequence.In Section 3,we prove the main theorems.
2 Compactness of(PS)cSequence
We recall from[5-7]the variational framework of nonsmooth critical point theory.
Let X be a complete metric space and f:X→R be a continuous function and u∈X.We denote by|df|(u)the supremum of the σ’s in[0,+∞)such that there exist δ>0 and a continuous map η:B(u;δ)×[0,δ]→X such that

The extended real number|df|(u)is called the weak slope of f at u.
We say that a point u∈X is a critical point if|df|(u)=0 and that a real number c∈R is a critical value of f if there exists a critical point u∈X of f with f(u)=c.
Let c∈R.We say that f satisfies the(nonsmooth)Palais-Smale condition at level c((PC)cin short),if every sequence{un}in X with|df|(un)→0 and f(un)→c contains a subsequence converging in X.
Under the above conceptions,the classical mountain pass theorem can be extended to nonsmooth case.
Theorem 2.1Let X be a Banach space endowed with the norm‖·‖,f:X→R a continuous function.Suppose that there exist w∈X,η>f(0)and r>0 such that
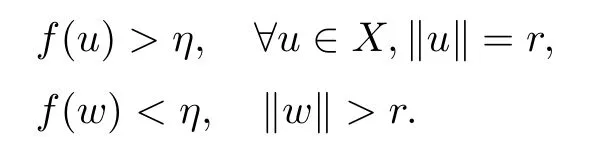
Setting Γ={γ:[0,1]→X,γ is continuous and γ(0)=0,γ(1)=w}.Suppose that f satisfies(PS)ccondition at the level
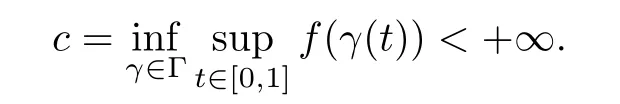
Then,there exists a nontrivial critical point u of f such that f(u)=c.
In order to prove that the functional I satisfies the(PS)ccondition,we introduce the following Concrete-Palais-Smale condition like[5].
De finition 2.2We say that a sequence(un)⊂X is a Concrete-Palais-Smale sequence of I at level c((CPS)cin short)if there exist(yn)⊂X∗with yn→0 such that I(un)→c and

We say that I satisfies the(CPS)ccondition if every(CPS)csequence is strongly compact in X.
Note that(2.1)holds for test function φ∈X∩L∝(RN)by approximation.In general,the(CPS)ccondition is not equal to the(PS)ccondition.The relationship between them can be elucidated by the following lemma.
ProofThe proof is similar to that for[5,Theorem 2.1.3].
Let(un)⊂X be a(PS)csequence of I,Lemma 2.3 means that it is also a(CPS)csequence of I,and thus admits a convergent subsequence,thus I satisfies the(PS)ccondition.In view of this,we should only prove that I satisfies the(CPS)ccondition.
We devote the rest of this section to study the compactness of the(CPS)csequence of I.
Proposition 2.4Assume that(a1)-(a3),(c)hold,then every(CPS)csequence{un}of I is bounded in X.
ProofFor every n∈N,we denote

and
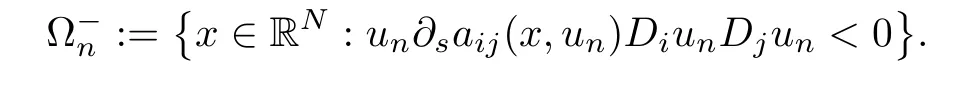
From(a2)-(a3),we obtain that
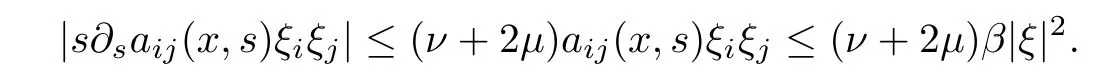
Thus un∂saij(x,un)DiunDjun∈L1(RN).Then,by approximation,we can take φ=unas test functions in(2.1)and get
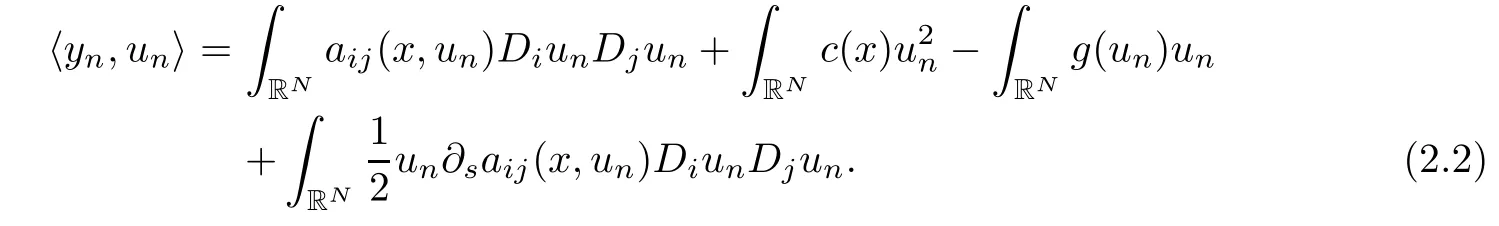
It is obvious that

Thus by(a3),we get


Taking(a2)and(2.3)into considering,the calculation of qI(un)−〈yn,un〉gives

This implies the conclusion of the proposition.
Now we prove the almost everywhere convergence of gradients of a bounded(CPS)csequence of I.We denote Du=(D1u,···,DNu).
Proposition 2.5Assume that(a1)-(a3),(c)hold,then for every bounded(CPS)csequence{un}of I,there exists u∈X such that Dun(x)→Du(x)a.e.in RN.
ProofThe proof is similar to that in[26,Theorem 2.1].Note that the imbedding from X into Lp(RN)is continuous for 1≤p≤2∗,is compact for 1≤p<2∗,and that{un}is bounded in X,there exists u∈X such that un⇀u in X,un→u in Lr(RN),1≤r<2∗and un→u a.e.in RN.Now let K,K′be two compact subsets of RNsuch that K′⊂⊂K⊂RN.Let φK∈[0,1]be a smooth function on RNsuch that φK=1 on K′and φK=0 on RNK.For k∈R,let Tkbe a truncated function with Tk(s)=s for|s|≤k and Tk(s)=ks/|s|for|s|>k.We take φ=φKTk(un−u)∈X as test functions in(2.1).Then by(a2)we deduce that

By(a1)-(a3)and note that q∈(2,2∗),we can estimate thatfor some constant C>0 and that II+III+IV+V+VI→0 as n→∞.In fact,since unis bounded in X,by(a1),we have∂saij(x,un)DiunDjunis bounded in L1(RN),thus
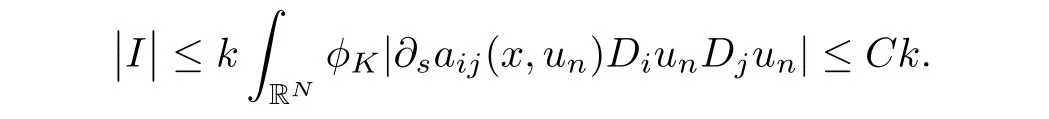
On the other hand,note that un⇀u in X,and un→u a.e.in RN,we have


The proof of III→0 is similar.Finally,since un→u in L2(K)and Lq(K),we have
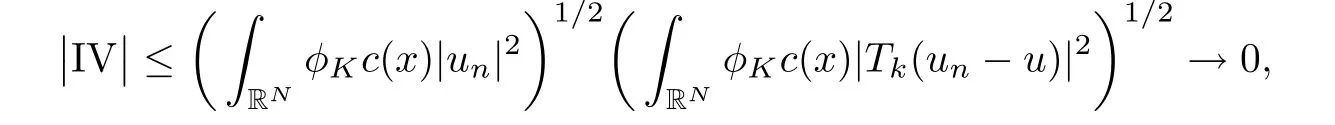
and similarly,
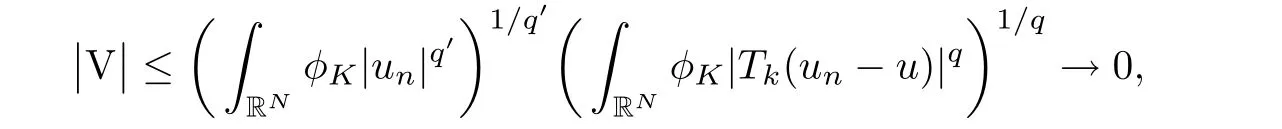
where q′=q/(q−1).VI→0 obviously.In conclusion,we have

De fi ne Ak,n:={x∈K:|un(x)−u(x)|>k},Bk,n=KAk,n.Then|Ak,n|→0 as n→∞since un(x)→u(x)a.e.in K.Let
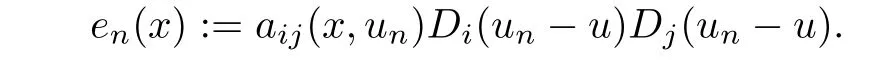
Then for 0<s<1,by Hölder inequality,we have
Combining this and(2.4),we obtain,as k→0,

which implies that en(x)→0 a.e.in K.Thus we conclude that Dun→Du in L2(K),which implies also that Dun(x)→Du(x)a.e.in K.
Now covering RNwith a sequence of compact sets with finite measure,we thus deduce that Dun(x)→Du(x)a.e.in RN.
Proposition 2.6Assume that(a1)-(a3),(c)hold,then every bounded(CPS)csequence {un}of I converges strongly in X to u∈X.
ProofBy Proposition 2.5,we have Dun(x)→Du(x)a.e.in RN,this make it possible for us to use special test functions and employ Fatou’s lemma to prove,like[11,Lemma 2.3],that
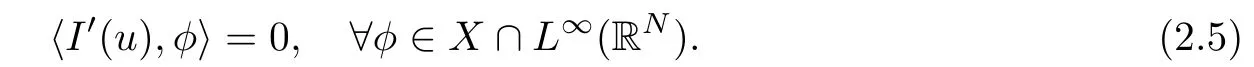
We present the proof of(2.5)in the end of this section for the sake of completeness.Especially,we have〈I′(u),u〉=0 by approximation.Then by a standard argument,we can prove that unconverges strongly to u in X.
In fact,first,from(2.2),we have

Note that we have〈yn,un〉→0,and that the imbedding XLq(RN)is compact,we have
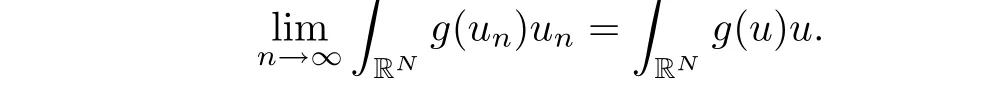
Moreover,(a3)implies that

So that we can employ Fatou’s lemma to deduce from(2.6)and〈I′(u),u〉=0 that

Second,by Fatou’s lemma,


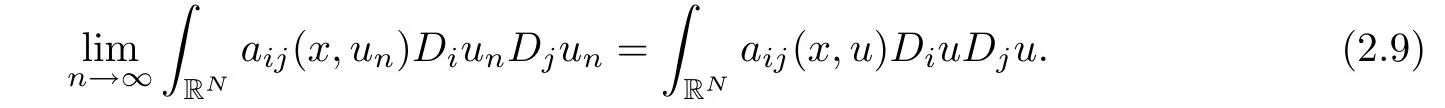
Likewise,we have
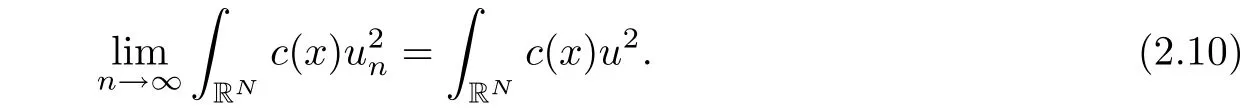
Third,since aij∈L∝(RN×R),by Lebesgue’s dominated convergence theorem,we have
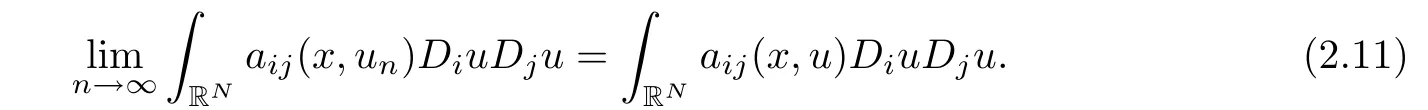
We claim that
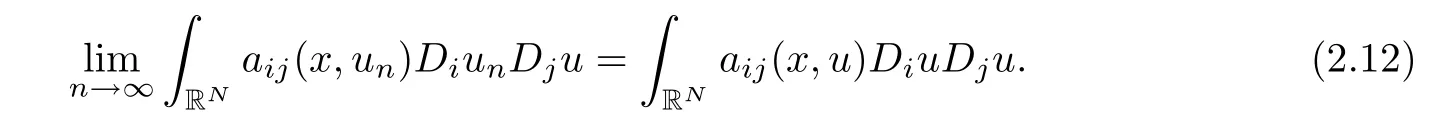
In fact,by Lebesgue’s dominated convergence theorem,for 1≤i,j≤N,we have

strongly in L2(RN).Thus Hölder’s inequality gives

Since by the weak convergence of un⇀u in X,

thus we conclude that(2.12)hold.
Finally,by the weak convergence of un⇀u in X,we have

Through the above analysis,we conclude from(2.9)-(2.13)that

This implies the strong convergence of{un}and completes the proof.
Remark 2.7Assume that(a1)-(a3)and(c)hold,{un}is a bounded(CPS)csequence of I converges weakly to u∈X.Then by an argument similar to the proof of(2.9)and(2.10),we can prove that

In fact,on one hand,the convergence of g(un)un→g(u)u in L1(RN),yn→0 in X∗,and(2.9)-(2.10)imply that
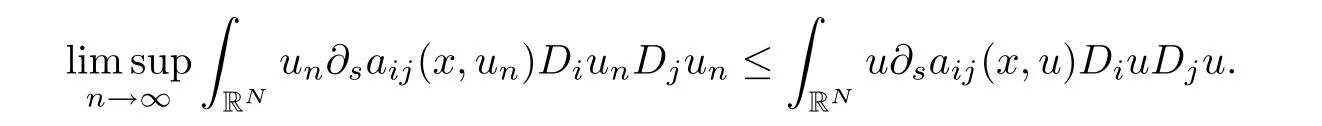
On the other hand,(2.7)ensures that we can employ Fatou’s lemma and(2.9)to deduce that
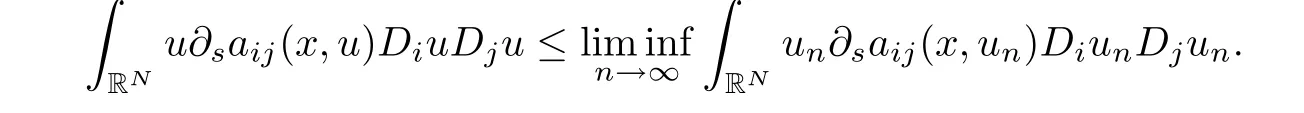
Now we prove equality(2.5).The crucial point is to dominate the integral
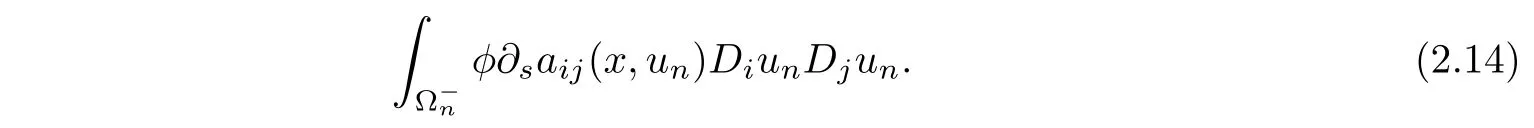
This can be done by modifying the test functionin[5],where ϕ∈X∩ L∝(RN)and M>0 sufficiently large.
Proof of(2.5)Let H∈[0,1]be a smooth cuto ff function on R withH=0 outside[−1,1],and|H′|≤C for some constant C>0.De fi ne s+=max{s,0},s−=

Note that

and by(a2),
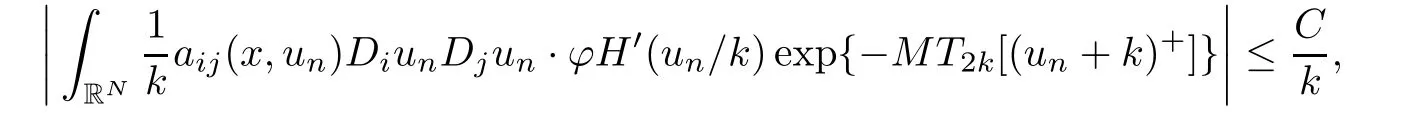
by Fatou’s lemma,we can take limsup in(2.15)and get
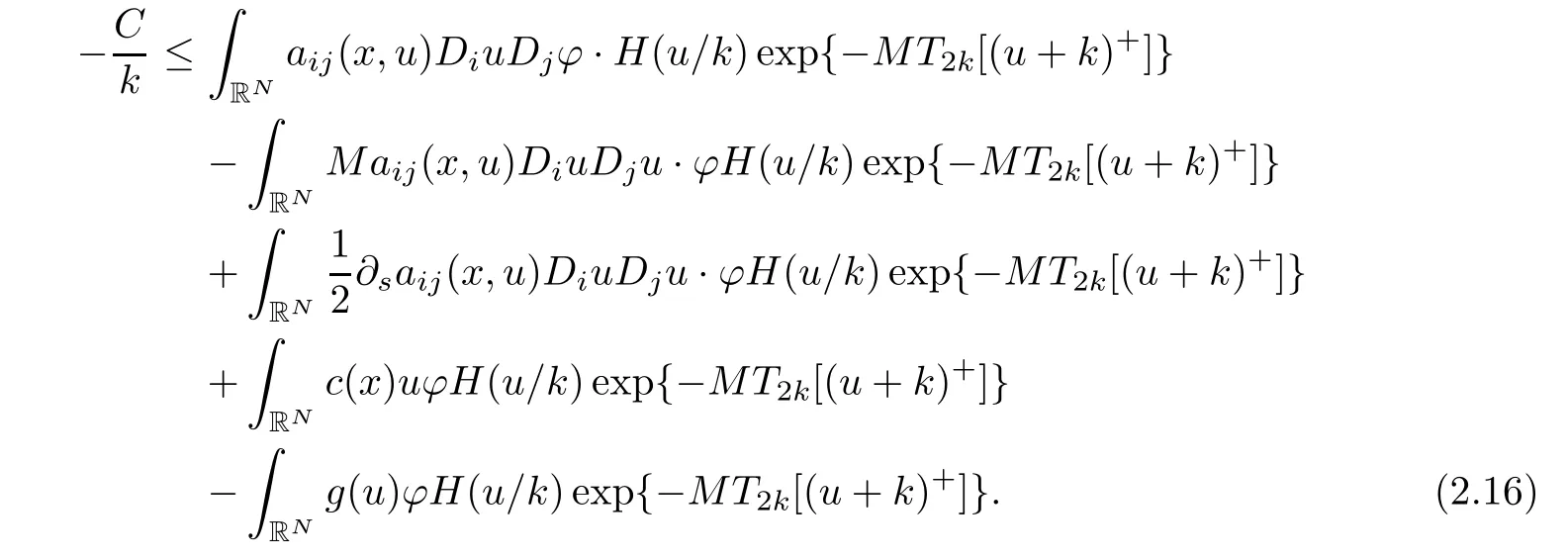
Choose ϕexp{MT2k[(u+k)+]}instead of ϕ in(2.16),and then let k→∞,we get

Now we take φ=ϕH(un/k)exp{−MT2k[(un−k)−]}in(2.1)to obtain the opposite inequality.Thus we have〈I′(u),ϕ〉=0 holds for ϕ≥0 and holds for ϕ≤0 similarly.Then it holds also for general ϕ∈X∩L∝(RN)by approximation.
Remark 2.8The main idea of the proof of(2.5)is to truncate the part in(2.14)that is out of control.Note that DjTk(un)≡0 on the set Ak,n(RN):={x∈RN:|un(x)−u(x)|>k}.Another method to prove(2.5)is to add additional integral of the principal part to dominate

Thus we can take φ as test function in(2.1)and obtain(2.5)similarly.
3 Proof of Main Results
In this section,we prove the existence and nonexistence of weak solutions of(1.1).
Proof of Theorem 1.1Theorem 2.1 applied.First,Proposition 2.6 shows that I satisfies(PS)ccondition.Secondly,we prove that I has the geometrical conditions stated in Theorem 2.1.In fact,we have I(0)=0.For every u∈X,by(a2)and Sobolev’s inequality,we have
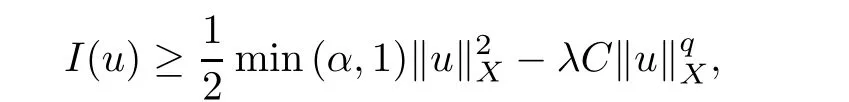
where C>0 is a constant.Thus there exist r>0,δ>0 such that I(u)≥δ for‖u‖X=r.Now let ϕ0∈X be such that ϕ0(x)>0 and‖ϕ0‖X=1 and let t∈R+,then by(a2)again,
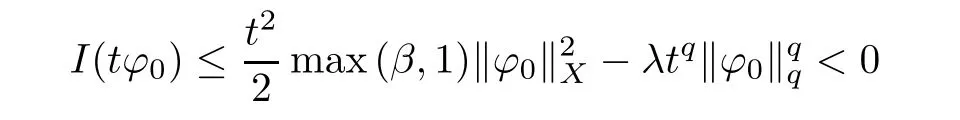
for t large.According to Theorem 2.1,I admit a critical point u∈X.
Remark 3.1(i)Denote u+=max{u,0}.Replacing|u|q−2u by|u|q−2u+in eq.(1.1),the solutions to the equation can be proved to be nonnegative.
(ii)Note that the measure of the set Ak={x∈RN:|u(x)|>k}is finite for k>0,the solution to(1.1)is in fact belongs to X∩L∝(RN).Indeed,if 2≤q<2∗,it can be deduced as in[12].If q=2∗,the same device as the proof for Theorem 4.1 in[18]can be applied.
In order to prove the nonexistence result Theorem 1.2,we empoy Pohozaev’s identity in[27](see also[28]).
Let Ω⊂RNbe open and F(x,u,r):be a functional of class C1,we consider the following equation
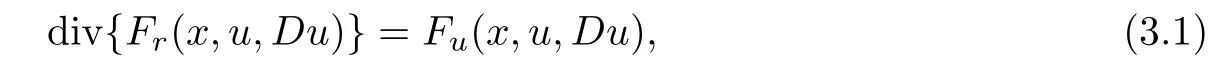
here we write Du=(∂u/∂x1,···,∂u/∂xN),Fu=∂F/∂u,Fxi=∂F/∂xiand Fri=∂F/∂ri,r=(r1,···,rN).Assume that F(x,0,0)=0.andbe a solution to problem(3.1),then we have the following Pohozaev’s identity.
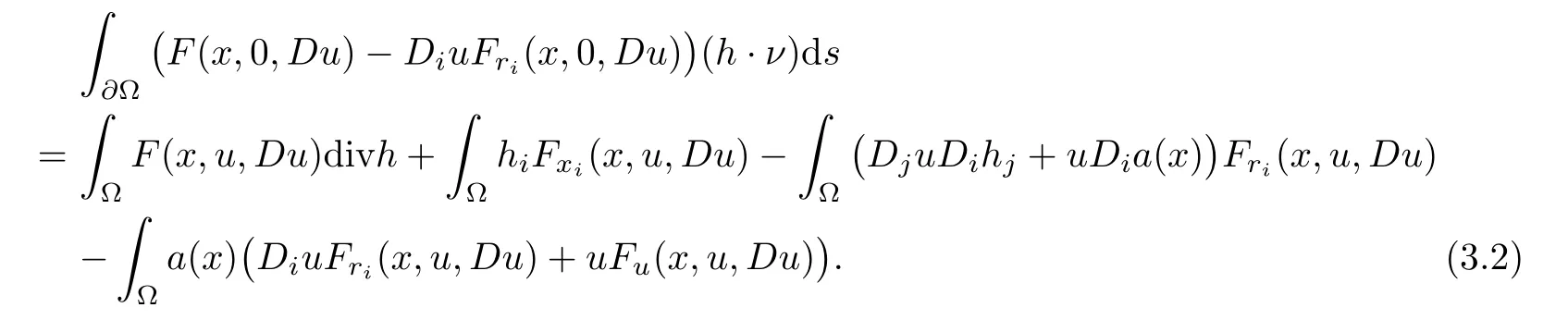
Proof of Theorem 1.2Assume on the contrary that u∈X∩C1(RN)is a weak solution to(1.1).Let

and let a be independent on x,h=x in(3.2),we get
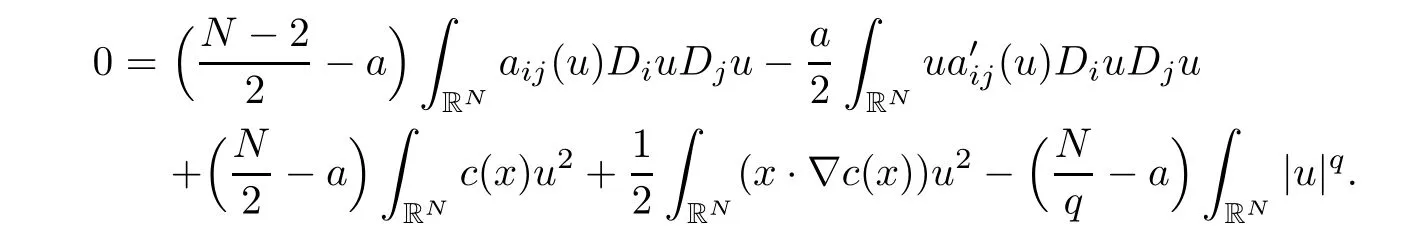
Set a=N/q.Note that by assumption,we havethus

Therefore if u satisfies(1.4),then(3.3)implies that u≡0.This completes the proof.
Remark 3.2The parameterµin(a3)is,in fact,should not greater thanaccording to Theorem 1.2.Moreover,as q tends to 2∗,µtends to 0.This is partially consistent with[10,Theorem 5.1],where the following result was proved:if bij(s),∂sbij(s)∈L∝(R),bij(s)ξiξj≥γ|ξ|2,γ∈(0,1]and s∂sbij(s)ξiξj<0,∀s0,then the equation

has no nontrivial solution inwhere Ω⊂RN(N≥3)is bounded and starshaped.
Now we are ready to prove Theorem 1.4.We prove that problem(1.3)has nontrivial solutions even if κ is less than zero.
Proof of Theorem 1.4By direct computation,we have

and
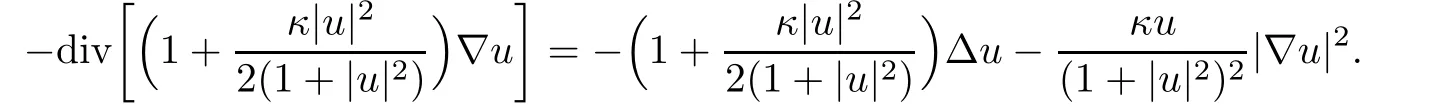
Thus we get

Case κ≥0.We prove that
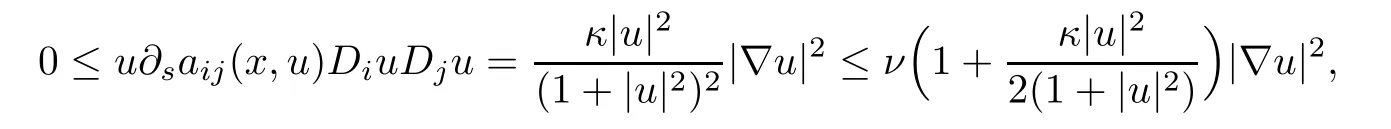
that is,
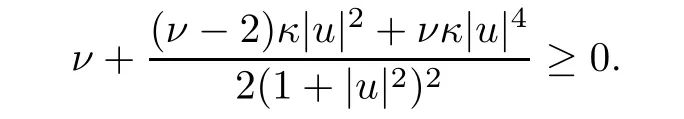
This inequality holds either(i)ν≥2 and κ≥0 or(ii)0<ν<2 andSinceis increasing in ν∈(0,2)and tends to+∞as ν tends to 2,we thus draw a conclusion that the inequality holds either(i)q≥4 and κ≥0 or(ii)2<q<4 and
Case κ<0.We prove that

that is,
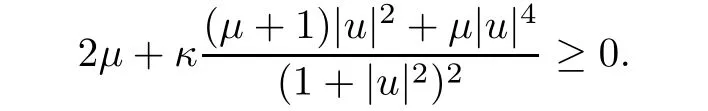

Proof of Corollary 1.7Under the assumptions of Corollary 1.7,assume that there is still a solution 0u∈X∩C1(RN)to(1.3).Then Pohozaev’s inequality,with a=N/2∗and h=x in(3.2),implies that

AcknowledgementsThe first author thanks the sta ff of Chern Institute of Mathematical,Nankai University and Professor Zhiqiang Wang for their hospitality.Part of this work was done when the first author was visiting there.
References
[1]Borovskii A V,Galkin A L.Dynamical modulation of an ultrashort high-intensity laser pulse in matter.JETP,1993,77:562-573
[2]Aouaoui S.Multiplicity of solutions for quasilinear elliptic equations in RN.J Math Anal Appl,2010,370:639-648
[3]Bartsch T,Pankov A,Wang Z Q.Nonlinear Schrödinger equations with steep potential well.Comm Contemp Math,2001,4:549-569
[4]do O J M,Severo U.Quasilinear Schrödinger equations involving concave and convex nonlinearities.Comm Pure Appl Anal,2009,8:621-644
[5]Canino A,Degiovanni M.Nonsmooth critical point theory and quasilinear elliptic equations//Granas A,Frigon M,Sabidussi G,eds.Topological Methods in Di ff erential Equations and Inclusions,Montreal,1994,NATO ASI Series.Dordrecht:Kluwer Academic Publishers,1995:1-50
[6]Corvellec J N,Degiovanni M,Marzocchi M.Deformation properties for continuous functionals and critical point theory.Topol Methods Nonl Anal,1993,1:151-171
[7]Degiovanni M,Marzocchi M.A critical point theory for nonsmooth functional.Ann Mat Pura Appl,1994,167(4):73-100
[8]Arcoya D,Boccardo L.Critical points for multiple integrals of the calculus of variations.Arch Rational Meth Anal,1996,134:249-274
[9]Arcoya D,Boccardo L,Orsina L.Existence of critical points for some noncoercive functionals.Ann I H Poincaré-AN,2001,18(4):437-457
[10]Arioli G,Gazzola F.Quasilinear elliptic equations at critical growth.NoDEA Nonl Ei ff er Equ Appl,1998,5:83-97
[11]Canino A.Multiplicity of solutions for quasilinear elliptic equations.Topol Methods Nonl Anal,1995,6:357-370
[12]Shen Y.Nontrivial solution for a class of quasilinear equation with natural growth.Acta Math Sinica,Chinese Series,2003,46:683-690
[13]Li Z,Shen Y,Yao Y.Nontrivial solutions for quasilinear elliptic equations with natural growth.Acta Math Sinica,Chinese Series,2009,52:785-798
[14]Shen Y,Li Z,Wang Y.Sign-changing critical points for noncoercive functionals.Topol Methods Nonl Anal,2014,43:373-384
[15]Squassina M.Existence,multiplicity,perturbation,and concentration results for a class of quasi-linear elliptic problems.Electronic Journal of Di ff erential Equations,Monograph 7,2006
[16]Abdellaoui B,Boccardo L,Peral I,et al.Quasilinear elliptic equations with natural growth.Di ff er Integr Equ,2007,20:1005-1020
[17]Boccardo L,Spagnolo S.Positive solutions for some quasilinear elliptic equations with natural growths.Rend Mat Acc Lincei,2000,11:31-39
[18]Li Z.Existence of nontrivial solutions for quasilinear elliptic equations at critical growth.Appl Math Comput,2011,218:76-87
[19]Pellacci B,Squassina M.Unbounded critical points for a class of lower semicontinuous functionals.J Di ff er Equ,2004,201:25-62
[20]Arioli G,Gazzola F.On a quasilinear elliptic differential equation in unbounded domains.Rend Istit Mat Univ,Trieste,1998,30:113-128
[21]Conti M,Gazzola F.Positive entire solutions of quasilinear elliptic problems via nonsmooth critical point theory.Topol Methods Nonl Anal,1996,8:275-294
[22]Gazzola F.Positive solutions of critical quasilinear elliptic problems in general domains.Abstr Appl Anal,1998,3(1/2):65-84
[23]Liu J Q,Wang Z Q,Guo Y X.Multibump solutions for quasilinear elliptic equations.J Funct Anal,2012,262:4040-4102
[24]Shen Y,Wang Y.Soliton solutions for generalized quasilinear Schr´odinger.Nonl Anal TMA,2013,80:194-201
[25]Li Z,Shen Y,Zhang Y.An application of nonsmooth critical point theory.Topol Methods Nonl Anal,2010,35:203-219
[26]Boccardo L,Murat F.Almost everywhere convergence of the gradients of solutions to elliptic and parabolic equations.Nonl Anal TMA,1992,19:581-597
[27]Pucci P,Serrin J.A general variational identity.Indiana Univ Math J,1986,35(3):681-703
[28]Degiovanni M,Musesti A,Squassina M.On the regularity of solutions in the Pucci-Serrin identity.Calc Var Partial Di ff erential Equations,2003,18:317-334
 Acta Mathematica Scientia(English Series)2016年1期
Acta Mathematica Scientia(English Series)2016年1期
- Acta Mathematica Scientia(English Series)的其它文章
- SOME STABILITY RESULTS FOR TIMOSHENKO SYSTEMS WITH COOPERATIVE FRICTIONAL AND INFINITE-MEMORY DAMPINGS IN THE DISPLACEMENT∗
- STABILITY OF VISCOUS SHOCK WAVES FOR THE ONE-DIMENSIONAL COMPRESSIBLE NAVIER-STOKES E QUATIONS WITH DENSITY-DEPENDENT VISCOSITY∗
- STABILITY ANALYSIS OF A COMPUTER VIRUS PROPAGATION MODEL WITH ANTIDOTE IN VULNERABLE SYSTEM∗
- STABILITY OF A PREDATOR-PREY SYSTEM WITH PREY TAXIS IN A GENERAL CLASS OF FUNCTIONAL RESPONSES∗
- NORMAL FAMILIES OF MEROMORPHIC FUNCTIONS WITH SHARED VALUES∗
- EDELSTEIN-SUZUKI-TYPE RESULTS FOR SELF-MAPPINGS IN VARIOUS ABSTRACT SPACES WITH APPLICATION TO FUNCTIONAL EQUATIONS∗
