凯撒问题的哲学意义

刘靖贤（辽宁大学哲学与公共管理学院，辽宁沈阳110136）



凯撒问题的哲学意义

刘靖贤
（辽宁大学哲学与公共管理学院，辽宁沈阳110136）

摘要：凯撒问题是当代分析哲学中的热门话题，许多学者都尝试为凯撒问题提供解决方案，林奈博给出关于区分范畴种类的元语义学方案、乌兹奎亚纳给出关于区分必然对象和偶然对象的模态方案、库克给出关于区分抽象原则的等价关系和等价类方案。然而，这些方案都不能最终解决凯撒问题。凯撒问题的哲学意义在于解决这个问题的尝试为我们带来了新的研究方法和新的研究方向，从而把分析哲学的研究引向深入。

关键词：凯撒问题；元语义学；必然对象；抽象原则

弗雷格的哲学目标是为了探求算术真理的本体论和认识论地位，他在语言哲学方面的工作（例如涵义和指称的区分）以及在逻辑哲学方面的工作（例如概念和对象的区分）事实上都是为了这个数学哲学的目标而服务的。他认为，所有算术符号都可以通过逻辑符号定义出来，所有的算术语句都可以从逻辑语句推导出来，所以算术真理既不依赖于直观，也不依赖于经验，而是仅仅依赖于理性。然而，弗雷格在定义算术符号时遇到了所谓的凯撒问题。

凯撒问题是说，如何确定凯撒这个人是不是3这个数。[1]从直观上看，这个问题是简单的，任何具有基本常识的人都知道凯撒这个人不是3这个数；但是在弗雷格那里，这是一个非常困难的问题，无论是概念分析的方法还是形式系统的方法，都不能解决凯撒问题。特别地，弗雷格建议通过休谟原则给出数的定义，休谟原则是说，属于概念F的数与属于概念G的数相等当且仅当F与G等数，

其中#是数算子，把一个概念映为属于这个概念的数，»是等数关系，表示存在两个概念之间的一一对应。但是，根据弗雷格的解释，对于任意变元x来说，休谟原则不能确定同一陈述x = #F的真值。如果x是属于某个概念的数，即x形如#G，那么休谟原则可以确定x = #F的真值；如果x不是属于某个概念的数，即x并非形如#G，那么休谟原则不能确定x = #F的真值。

凯撒问题是当代分析哲学中的热门话题，许多学者都尝试为凯撒问题提供解决方案，虽然所有这些解决方案都隐含着某种假设，这些假设都在某种程度上有不合理之处，但是凯撒问题的哲学意义并不在于这个问题是否得到最终解决，而是在于解决这个问题的尝试是否为我们带来了新的研究方法和新的研究方向，从而把分析哲学的研究引向深入。本文将讨论三种新近的关于凯撒问题的解决方案：林奈博关于区分范畴种类的元语义学方案、乌兹奎亚纳关于区分必然对象和偶然对象的模态方案、库克关于区分抽象原则的等价关系和等价类方案。在评述这些解决方案的基础上，我将揭示凯撒问题的哲学意义，特别是它对当代分析哲学的深远影响。

一、林奈博关于区分范畴种类的元语义学方案

林奈博认为，凯撒问题的解决必须依赖于我们关于人范畴和数范畴区分的直观，但是这个直观在弗雷格的概念分析中被瓦解了。在林奈博看来，弗雷格在《算术基础》中对数的概念分析是建立在如下原则基础上的：为了全面理解一个单称词项a，人们需要拥有适用于a的同一标准。这个原则被称为弗雷格原则。什么是同一标准？如何给出同一标准？或者说，如何确定同一陈述的真值条件？

根据现代语义学，真值条件是由如下原则确定的：一个语句S的真值条件直接包含所有外延地出现在S中的单称词项的指称，这些指称的名称必须外延地出现在S真值条件的元语言刻画中。这个原则被称为真值条件包含指称原则（Truth-condition Involve Referents），它在实质上是组合原则的特例。在这个一般原则的指导下，有两种关于同一标准的观点。一种观点被称为极小主义观点：包含两个单称词项的同一陈述是真的，当且仅当，它们的指称是相同，即

但是这种观点完全没有提供任何信息，仅仅把语法问题转化为语义问题。另一种观点被称为形而上学观点：任给分类概念F中的两个对象，它们的同一标准是它们处于某个等价关系中，即

然而，形而上学观点把同一问题转化为更复杂的等价关系问题，难道任何概念都对应于一个等价关系吗？因此，无论极小主义观点还是形而上学观点都不能合理地说明同一问题，这似乎表明，弗雷格原则与真值条件包含指称原则是相互矛盾的，也就是说，凯撒问题的困难来源于一个两难困境：一方面，为了知道包含两个单称词项的同一陈述的真值条件必须已经知道这两个单称词项指称什么对象；另一方面，弗雷格原则要求，理解单称词项如何指称的关键在于已经知道适用于这些单称词项的同一标准。

林奈博通过语义学和元语义学的区分来消解这个困境。[2]语义学说明，复杂表达式的语义值如何依赖于其简单成分的语义值，语义结构作为一个语义函数通过简单成分的语义值确定复杂表达式的语义值；而元语义学（meta-semantics）说明，为什么一个表达式具有特定的语义性质，由于什么原因一个表达式具有它的语义结构和语义值。从这个角度看，真值条件包含指称原则是一个语义原则，而弗雷格原则是一个元语义原则，因为前者假定简单表达式都有适当的语义值，它们确定了复杂表达式的真值条件，而后者通过同一标准来解释单称词项之所以指称对象的原因。因此，根据语义学和元语义学之间的区分，真值条件包含指称原则和弗雷格原则分别处于不同的层次，它们之间不存在冲突。凯撒问题虽然披着语义学的外衣，但它实质上是一个元语义学问题。

根据元语义学观点，单称词项的指称包含两个要素：指称媒介（referential intermediaries）和统一关系（unity relations）。前者说明指称的呈现方式，后者说明两个指称媒介的同一标准。林奈博把指称媒介和统一关系构成的序对称为指称尝试（referential attempt）。假设a是一个单称词项，其指称尝试是（u，R），其中u确定指称是如何呈现的，R确定两个指称是否相同。再假设b也是一个单称词项，其指称尝试是（v，R），而且a和b指称相同种类的对象。通过如下条件可以解释一个单称词项如何指称：

这被称为归约真值条件（reduced truth-condition），事实上，它定义了一个函数f，

这被称为个体原则，其中f把一个指称媒介映为一个指称。因此，语义学是语词与其指称之间的桥梁，它解释一个语词指称什么对象，而元语义学是指称与其指称尝试之间的桥梁，它解释一个语词为什么指称一个对象。

根据指称尝试这个辅助手段，如果我们理解归约真值条件，那么我们不仅能够追溯a的指称，也能够把它与其他同类对象区分开来。然而，所有对象都与指称尝试有关吗？日常经验给出的答案似乎是否定的。有些对象是直接通过知觉给予我们的，例如，在看到和摸到一块石头时，我们识别出这块石头；但是有些对象不能直接通过知觉给予我们，而是需要某些辅助概念，例如，为了识别出一块石头的下半部分，我们需要凭借“下”、“半”这些概念。林奈博把前者称为自然对象，把后者称为非自然对象。针对这种区别，他提出了一个根本性的观点：所有对象都是通过某种概念化过程才给予我们的，有些时候我们意识到这个过程，但有些时候没有意识到这个过程。即使对于自然对象来说，虽然我们直接知觉到一块石头，但是为了指称这块石头，我们需要以时空部分为媒介，我们与时空部分处于因果关系中，而且我们通过时空的连续性来识别这块石头与其他石头的同一和差异。因此，所有对象的指称都需要指称媒介和统一关系，也就是说，任何对象的指称都依赖于从元语义学角度给出的指称尝试。

在林奈博看来，不同的范畴种类对应于不同的指称尝试，例如，方向的指称媒介是直线，方向相同当且仅当直线平行；形状的媒介是轮廓，形状相同当且仅当轮廓重叠；语法类型的媒介是标记，类型相同当且仅当标记相同；数的指称媒介是数词在序列中的位置，数相同当且仅当数词的位置相似；集合的指称媒介是元素，集合相同当且仅当构成的元素相同；物体的指称媒介是时空部分，物体相同当且仅当时空部分以某种适当的方式是连续的。根据元语义学，林奈博给出了范畴的定义。首先，一个谓词是分类的（sortal），当且仅当，其涵义关联于某个指称媒介和某个统一关系。换言之，从直观角度看，一个谓词是分类的，当且仅当，这个谓词在使用中需要不定冠词。例如，我们说约翰是一只猫，但是我们不说约翰是一个“重”，所以猫是分类谓词，但是“重”不是分类谓词。其次，一个分类谓词F是极大的，当且仅当，不存在其他分类谓词包含在F中，而且它们关联于相同的指称媒介和相同的统一关系。最后，范畴被定义为极大的分类谓词。根据上述定义，不同范畴之间不存在重合，一个范畴规定了隶属于这个范畴的对象的本质。因此，对于凯撒问题来说，“凯撒这个人是不是3这个数”不是一个内范畴同一陈述，而是一个跨范畴同一陈述，所有跨范畴同一陈述的真值都是假。

在我看来，林奈博的方案没有从根本上解决凯撒问题。他强调所有对象的指称都依赖于某个概念化过程或某个指称尝试，但他忽视了同一个对象的认识过程有可能依赖于不同的概念化过程或不同的指称尝试。正如弗雷格所说，“对象的给出方式不是对象的固有性质”[3]，同一个对象既可以通过这样的方式给出，也可以通过那样的方式给出。例如，弗雷格明确提到，真值既可以通过对象的方式给出，也可以通过集合的方式给出。[3]如果以对象的方式给出，那么两个真值a和b的指称尝试分别是（s，R1）和（t，R1），其中s和t是命题，R1是命题之间的等价关系，也就是说，a这个真值b和这个真值相等，当且仅当，s这个命题和t这个命题等价。如果以集合的方式给出，例如真值被看做它们自身的单元集，那么两个真值a和b的指称尝试分别是（m，R2）和（n，R2），其中m和n是单元集，R2是集合之间的相等关系，也就是说，a这个真值b和这个真值相等，当且仅当，m这个集合与n这个集合相等。由此可见，相同种类的对象以不同方式给出，很难确定究竟哪个范畴描述了这个对象的本质，也就是说，很难确定究竟真值隶属于命题的范畴还是单元集的范畴，在这种情况下跨范畴同一问题仍然是无法解决的问题。

二、乌兹奎亚纳关于区分抽象对象和具体对象的模态论证

虽然同样面对凯撒问题，但是与林奈博不同，乌兹奎亚纳思考的出发点是，为什么算术语词的日常使用能够排除凯撒这样物理对象作为数词的指称。在乌氏看来，数学对象和物理对象的区别在于，前者是必然对象，而后者是偶然对象，所以解决凯撒问题的关键在于，如何区分必然对象和偶然对象。

在乌氏之前，泰南特曾经给出算术对象必然性的论证。[4]他首先给出数的定义：

为了论证算术对象的必然性，乌氏给出了一个全新的模态论证，[5]这个论证的直观背景是：不仅在现实情形中而且在反事实情形中我们都用数来计数落在一个概念中的对象的数目。我们以天王星的卫星为例。天王星的5颗主要卫星是：米兰达、艾瑞尔、乌姆柏里厄尔、泰坦尼亚和欧贝隆。乌氏从相关反事实情形出发，推出的结论是：艾瑞尔作为天王星的卫星之一（也作为物理对象或偶然对象）不是“4”这个数词的指称的候选者。首先，我们在反事实情形的设想中得出如下两个命题：

第一，如果艾瑞尔不存在，那么天王星恰好有4颗主要的卫星。

第二，如果天王星恰好有4个主要的卫星，那么天王星主要卫星的数是4。

其中第二要求4这个数即使在反事实情形中也能够计数天王星主要卫星的数目，也就是说，我们假设4这个数即使在反事实情形中也能够扮演它在现实应用中的角色。从第一和第二可以逻辑地得出：

第三，如果艾瑞尔不存在，那么天王星主要卫星的数是4。

显然，从“天王星主要卫星的数是4”可以推出“4存在”，也就是说，从a = 4可以推出$x(x = 4)。因此，从第三得到：

第四，如果艾瑞尔不存在，那么4仍然存在。

第四相当于说，存在一个可能世界，艾瑞尔不在其中存在，但是4在其中存在，所以有可能4不是艾瑞尔，即

经过假言易位和模态词转换，我们从（2.6）得到：

经过分离规则，从（2.5）和（2.7）得到：

因为4这个数不同于艾瑞尔这颗卫星，所以如果天王星主要卫星的数是4，那么天王星主要卫星的数不是艾瑞尔，也就是说“4”这个数词不能指称艾瑞尔。类似于上面推理，如果把“艾瑞尔”替换为“凯撒”，那么我们也可以得出结论：4这个数不同于凯撒这个人，“4”这个数词不能指称凯撒。

然而，乌氏认为，上述论证隐含了不合理的假设，即数词是严格指示词，“4”这个数词在任何可能世界中都指称相同的对象。我们在泰南特的论证中也看到这个不合理的假设。事实上，乌氏的论证并不实质性地依赖于“数词是严格指示词”这个假设，如果用概念词（描述词）来表示数词，即数词不是作为专名出现而是作为概念词出现，那么乌氏的论证仍然成立。首先，我们在反事实情形的设想中得出：

第九，存在一个数，它是天王星除艾瑞尔外主要卫星的数，而且如果艾瑞尔不存在，那么这个数也是天王星主要卫星的数。

这里的第九相当于前面的第三。类似于从第三得出第四，从第九得出：

第十，存在一个数，它是天王星除艾瑞尔外主要卫星的数，而且如果艾瑞尔不存在，那么这个数也存在。

类似于从第四得出第五，从第十得出：

第十一，存在一个数，它是天王星除艾瑞尔外主要卫星的数，而且它可能不同于艾瑞尔。

最后，类似于从第五得出第八，根据同一的必然性，从第十一得出

第十二，存在一个数，它是天王星主要卫星的数，而且它不同于艾瑞尔。

在上述论证中，“4”这个专名被替换为“存在一个如此这般的数”这个描述词。因此，乌氏的模态论证在实质上并不依赖于“数词是严格指示词”这个假设。基于乌氏的论证，我们可以得出一般性的结论：对于任何现实并且偶然的对象，例如伊丽莎白女王，4这个数不同于伊丽莎白女王，“4”这个数词不指称伊丽莎白女王；对于任何非现实但偶然的对象，例如飞马（Pegasus），4这个数不同于飞马，“4”这个数词不指称飞马。

在乌氏看来，上述论证反驳了所谓的语义唯名论。语义唯名论认为，虽然从语法上看，数词指称抽象对象，其他语词指称具体对象，但是从语义上看，根本不存在抽象对象，物理对象或偶然对象有资格成为数词的指称。因此，在语义唯名论看来，4这个数词有可能指称凯撒这个人。为了彻底反驳语义唯名论，乌氏设计了一个语义唯名论者可能采取的反驳策略，即把第九替换为：

第十三，存在一个数，它是天王星除艾瑞尔外主要卫星的数，而且如果艾瑞尔不存在，那么这个相同的数是天王星主要卫星的数。

其中“相同的数”是一个跨世界关系，它在不同世界中把相同的数词与不同的指称关联起来。例如，“4”在现实世界中指称凯撒，但是在另一个可能世界w中指称木星，w与现实世界几乎一样，唯一的例外是，凯撒在现实世界中存在，但是在w中不存在。如果这样，那么在现实世界中“4”指称凯撒，凯撒是木星卫星的数，但是在w中这个相同的数词指称木星，木星是木星卫星的数。如果这种改写成立，那么在不同的可能世界中，跨世界关系把的不同偶然对象赋予数词。所以即使在反事实情形的谈论中仍然不能排除偶然对象作为数词指称的候选者。然而，在乌氏看来，这个改写不符合我们在反事实情形中关于数词的用法，所以语义唯名论者不能反驳乌氏的模态论证。

在我看来，乌氏的方案也不能从根本上解决凯撒问题。乌氏本人也承认，数的本质在于同构性，即数在数序列中的位置。我们假设在任何可能世界中数的本质保持不变，所以只要保持数的本质不变，我们可以设想任何反事实情形。我将通过新的论证揭示乌氏模态方案的矛盾之处。以“大于等于1并且小于等于4”这个概念为例，恰好有4个对象落在这个概念中，即1、2、3、4。类似于第三，我们在反事实情形的设想中得出：

第十四，如果3不存在，那么“大于等于1并且小于等于4”这个概念的数是4。

因为在我们设想的可能世界w中3不存在，在自然数序列中，4占据了3的位置，所以w中4的本质是现实世界中3的本质。如果3不存在，那么落在“大于等于1并且小于等于4”这个概念中的对象的数目是3，即1、2、4，但是w中，因为4占据了3的位置，所以落在这个概念中的对象的数目是4。类似于从第三得到第四，从第十四得到：

第十五，如果3不存在，那么4仍然存在。

也就是说，在w中， 4不是3，但也正是在w中， 4是3，因为4占据了3的位置，矛盾。

三、库克关于区分抽象原则的等价关系和等价类方案

像休谟原则这样的抽象原则具有的一般形式是：

其中@是抽象算子，它把一个概念映为一个抽象对象，E( ,)是两个概念之间的等价关系。抽象原则通过两个概念之间的等价关系给出了两个抽象对象是否相等的充分必要条件。相应地，凯撒问题的一般形式是：对于任意变元x，抽象原则如何确定同一陈述x = @Y的真值。如果x是形如@X的抽象对象，那么抽象原则可以确定x = @Y的真值；如果x不是形如@X的抽象对象，那么抽象原则不能确定x = @Y的真值。在库克看来，即使x是抽象对象，某个版本的凯撒问题依然存在。对于如下两个抽象原则来说：

虽然@1F和@2P都是抽象对象，但是我们仍然不能确定的@1F = @2P真值。库克把这个版本的凯撒问题称为跨抽象原则的同一问题。他给出了两类解决方案。[6]

第一类解决方案是利用等价关系来确定抽象对象的同一。在库克看来，@1F与@2P是否相同的充分必要条件是E1(F,G)和E2(P,Q)是否表达了相同的等价关系，也就是说，@1F = @2P的充分必要条件

第一类解决方案是利用等价关系来确定抽象对象的同一。在库克看来，@1F与@2P是否相同的充分必要条件是E1(F,G)和E2(P,Q)是否表达了相同的等价关系，也就是说，@1F = @2P的充分必要条件是：

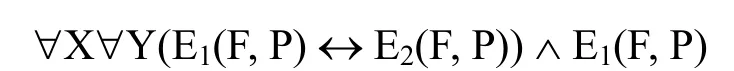
或者等价地，

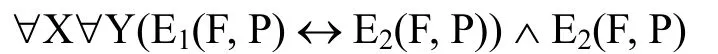
换言之，从两个概念得到的抽象对象是相同的，当且仅当，相应的等价关系是相同的并且这两个概念处于这个等价关系中。

第二类解决方案是利用等价类来确定抽象对象的同一。根据抽象原则，从一个概念F得到的抽象对象都关联于一个等价类，这个等价类包括所有其抽象对象与F的抽象对象相等的概念，也就是说，

因此，从一个概念F得到的抽象对象被定义为所有与F处于等价关系的概念的类。

库克在第二类方案的框架下给出了三个具体方案。第一，如果把抽象对象定义为等价类，那么因为等价类是类或集合，所以类或集合作为抽象对象也需要通过抽象原则给出同一标准。一般来说，类或集合的同一标准是：

其中{ :}是类算子，它把一个概念映为一个类或集合。这个同一标准恰好是弗雷格的第五公理。根据抽象原则，F的抽象对象被定义为：

也就是说，F的抽象对象被定义为与F具有等价关系的概念的抽象对象的类或集合。如果再给出P的抽象对象的定义：

那么根据抽象对象的定义，我们可以确定的@1F = @2P真值。第二，不把抽象对象定义为等价类，而是通过等价类给出抽象对象的同一标准：

也就是说，我们对抽象对象同一标准的理解先于对抽象对象本身的理解。第三，彻底放弃集合或类，把抽象对象的同一标准定义为等值式：

因为@1F = @1X等价于E1(F,X)，并且@2P = @2X等价于E2(F,X)，所以为了确定@1F = @2P的真值，即{X:@1F = @1X} = {X:@2P = @2X}的真值，仅仅需要确定{X:E1(F,X)} = {X:E2(F,X)}的真值，即X(E1(F,X)E2(P,X))的真值。

然而，库克的解决方案也不能从根本上解决凯撒问题。他的第一类解决方案诉诸于等价关系来区分抽象对象，但是等价关系不能把抽象对象完全区分开来。比较休谟原则和有穷休谟原则：

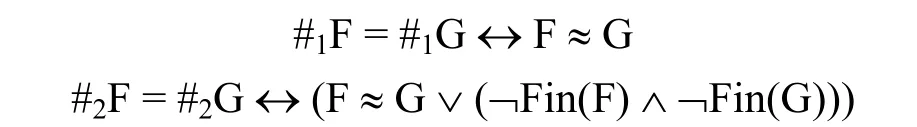
其中Fin(F)表示F是有穷概念，即仅仅有穷个对象落在F中。休谟原则是说，两个概念的数相等，当且仅当，这两个概念等数；而有穷休谟原则是说，如果两个概念都是有穷概念，那么这两个概念的数相等，当且仅当，这两个概念等数；如果两个概念都是无穷概念，那么这两个概念的数不足道地相等[7]。虽然对于有穷概念来说，从休谟原则和有穷休谟原则得到的抽象对象是相同，但是，对于无穷概念来说，从它们得到的抽象对象是不同的，因此，休谟原则和有穷休谟原则是不同的。但是，等价关系不能把休谟原则和有穷休谟原则完全区分开来。

在库克的第二类解决方案中，第一个具体方案把抽象对象定义为等价类，所以集合或类也可以被

定义为等价类：

也就是说，如果把集合或类也定义为等价类，那么一个集合相当于由这个集合构成的单元集，即a = {a}，这显然是不合理的。更为严重的是，第一个具体方案诉诸于第五公理，但是第五公理与二阶逻辑导致臭名昭著的罗素悖论，因此，从一致性角度看，第一个具体方案也是不合理的。虽然第二个具体方案没有直接诉诸于第五公理，但是在表述抽象对象同一标准时仍然使用了类算子，而第五公理是关于类算子的公理，所以，第二个具体方案也间接地使用了第五公理，也将导致罗素悖论。因此，从一致性角度看，第二个具体方案也是不合理的。第三个具体方案完全摆脱了类算子，但是仍然导致不合理的结果。比较休谟原则和第五公理：

根据第三个具体方案，数和类都是抽象对象，它们的区分标准是：

如果X是空概念，即任何对象都不落在其中的概念，那么因为F和X等数，所以F也是空概念，而且因为X和P等价，所以P也是空概念。由此得到：

也就是说，F的数和P的类是相等的，当且仅当，F和P都是空概念，换言之，因为空概念的数是0，而空概念的类是空类，所以只有0这个数和这个空类是相等的，任何其他数和其他类都是不相等的。显然，这是一个不合理的结果。

四、结语

与大多数哲学问题类似，凯撒问题的意义不在于它本身是否得到解决，而在于它是否把哲学研究引向更为深刻的维度。事实上，凯撒问题是一个全方位多角度的问题，不仅与形而上学有关， 而且与认识论有关，还与语义学有关。从语义学角度看，凯撒问题要求我们确定“3这个数是凯撒这个人”这个陈述的真值条件，也就是说，确定形如“a = b”这个等式的真值条件。从认识论角度看，凯撒问题要求我们的知识能够识别出3这个数和凯撒这个人的差异，也就是说，我们认识3这个数的过程不同于认识凯撒这个人的过程。从形而上学角度看，凯撒问题要求我们给出对象的同一标准，也就是说，把3这个数的本体论地位与凯撒这个人的本体论地位区分开来。

本文评述了凯撒问题的三种解决方案，虽然这些方案不能从根本上解决凯撒问题，但是它们把分析哲学的研究引向了更为深刻的维度。林奈博的方案把3和凯撒之间区分看做不同范畴之间的区分，并且通过元语义学给出范畴的刻画和定义。与语义学相比，元语义学通过指称媒介更为紧密地把语词和事物、符号和对象关联起来，这也更为深刻地触及到语言哲学的根本问题——语言和世界的关系。然而，仅凭指称媒介和统一关系还不能把握语言和世界的内在关联。乌兹奎亚纳的方案在模态形而上学中讨论凯撒问题，他把3和凯撒之间的区分看做必然对象和偶然对象之间的区分，然后，他在反事实设想中从“凯撒可能与3不同”推出“凯撒与3不同”，即凯撒不是“3”这个数词指称的候选者。然而，正如有可能不存在人，也有可能不存在数。反事实设想的界限在哪里？可设想蕴涵可能吗？这是关于可能世界的难题。库克把数学对象看做抽象对象，而抽象对象是通过抽象原则给出的，他把凯撒问题看做如何通过抽象原则来区分抽象对象的问题。抽象对象的本体论和认识论地位是数学哲学中的主要问题，他通过抽象原则解释抽象对象的做法为数学哲学的研究提供了新的角度。然而，对于他的方案来说，无论诉诸于等价关系还是诉诸于等价类，要么得出违反直观的结论，要么陷入罗素悖论的泥潭。

在我看来，凯撒问题不仅渗透到分析哲学的各个方面，而且也揭示出分析哲学本身的局限性。逻辑分析和哲学分析从亚里士多德到弗雷格经历了两千多年的发展演变，在这个过程中函数和主目（概念和对象）的分析取代了传统的主词和谓词的分析，其意义不亚于相对论和量子力学取代牛顿力学、非欧几何取代欧几里得几何。然而，亚里士多德的主词和谓词分析不仅保留了常识而且体现了直观，在亚里士多德的分析框架下，根本不存在凯撒问题，因为凭借直观和常识可以把人和数区分为不同的范畴。但是，弗雷格的哲学革命把直观和常识驱逐到哲学领域之外，一切哲学问题都在理性和推理的框架下展开讨论，当他通过概念和对象的分析来说明算术对象时，凯撒问题突显出来，而且时至今日依然是分析哲学中的难题。随着分析哲学研究的深入，将出现更多有关凯撒问题的解决方案，但是这个问题的根本解决必将迎来分析哲学中的又一次脱胎换骨的革命。

参考文献：

[1]Gottlob Frege.The Foundations of Arithmetic[M].trans.J.Austin,Blackwell:Blackwell,1950:77-78.

[2]Oystein Linnebo.To Be Is to Bean F[J].Dialectica,2005(59):201-222.

[3]Gottlob Frege.The Basic Laws of Arithmetic[M].trans.M.Furth.Berkeley:University of California Press,1964:48.

[4]Neil Tennant.On the Necessary ExistenceofNumbers[J].Nous,1997(31):307-336.

[5]GabrielUzquiano.Semantic Nominalism[J].Dialectica,2005(59):265-282.

[6]Roy Cook and Philip Ebert.Abstraction and Identity[J].Dialectica,2005(59):121-139.

[7]Richard Heck.Finitude and Hume’s Principle[J].Journalof Philosophical Logic,1997(26):589-617.

（责编：彭麟淋谭本龙郎禹叶莉责校：明茂修）

The Philosophical Significance of Caesar Problem

LIU Jing-xian
(College of Philosophy and Public Administration,Liaoning University,Shenyang,Liaoning110136,China)

Abstract:Caesar Problem is a hot topic in contemporary analytic philosophy.Many scholars try to pro⁃vide solutions to Caesar problem.Linnebo proposes meta-semantics to make a distinction between categories; Uzquiano suggests a modal differentiation between necessary objects and contingent objects; Cook offers crite⁃ria of equivalence relation and equivalence class.After showing all these methods cannot solve Caesar prob⁃lem,it points out that the philosophical significance of Caesar Problem is the new method and strategy which will promote the development of analytic philosophy.

Key words:Caesar Problem;Meta-semantics;Necessary Objects;Abstraction Principle

作者简介：刘靖贤（1982-），男，河北唐山人，辽宁大学哲学与公共管理学院讲师，美国布朗大学哲学系访问学者（2011年9月至2012年8月），哲学博士。研究方向：分析哲学。

基金项目：国家社科基金青年项目“弗雷格哲学著作编译研究”，项目编号：15CZX035。

收稿日期：2015-09-10

中图分类号：B81

文献标识码：A

文章编号：2096-0239（2016）01-0048-08