加权局部方差优化初始簇中心的K-means算法*
蔡宇浩,梁永全,樊建聪,李 璇,刘文华
加权局部方差优化初始簇中心的K-means算法*
蔡宇浩,梁永全,樊建聪+,李璇,刘文华
山东科技大学信息科学与工程学院,山东青岛266590
ISSN 1673-9418 CODEN JKYTA8
Journal of Frontiers of Computer Science and Technology 1673-9418/2016/10(05)-0732-10
http://www.ceaj.org Tel: +86-10-89056056
* The National Natural Science Foundation of China under Grant No. 61203305 (国家自然科学基金). Received 2015-09,Accepted 2015-11.
CNKI网络优先出版: 2015-11-24, http://www.cnki.net/kcms/detail/11.5602.TP.20151124.1354.002.htm l
CAI Yuhao, LIANG Yongquan, FAN Jiancong, et al. Optim izing initial cluster centroids by weighted local variance in K-meansalgorithm. Journal of Frontiersof Computer Scienceand Technology, 2016, 10(5):732-741.
摘要:在传统K-means算法中,初始簇中心选择的随机性,导致聚类结果随不同的聚类中心而不同。因此出现了很多簇中心的选择方法,但是很多已有的簇中心选择算法,其聚类结果受参数调节的影响较大。针对这
一问题,提出了一种新的初始簇中心选择算法,称为WLV-K-means(weighted local variance K-means)。该算法采用加权局部方差度量样本的密度,以更好地发现密度高的样本,并利用改进的最大最小法,启发式地选择簇初始中心点。在UCI数据集上的实验结果表明,WLV-K-means算法不仅能够取得较好的聚类结果,而且受参数变化的影响较小,有更加稳定的表现。
关键词:K-means算法;方差;加权;最大最小法;簇初始中心点
1 引言
聚类是一种无监督的学习方法,主要目的是把数据对象划分为多个不同的簇或者子集,使得同一簇内的样本彼此之间具有较高的相似度,而不同簇的样本之间相似度较低。聚类的实用性得到了非常广泛的认可,应用领域也很多,包括商务智能、图像识别、Web搜索、生物学和信息安全等。常用的聚类方法根据其特性可以被划分为划分方法、层次方法、基于密度的方法、基于网格的方法等[1]。
K-means算法[2]是一种应用广泛的基于划分的聚类方法,具有简洁、通用以及快速等优点。然而传统K-means算法中,初始中心点的随机选取,将导致聚类结果随初始点的不同而不同。如果选择的初始中心点导致算法收敛至局部最优,聚类结果可能会很不理想[3]。
针对K-means算法的缺点,以及K中心点选择优化算法中存在的问题[4],本文从两个方面进行改进:(1)定义了加权局部方差作为样本密度衡量的标准;(2)改进了最大最小法,进一步选择密度大且分隔较远的初始中心点。
本文组织结构如下:第2章介绍优化初始中心点K-means算法近期的相关工作;第3章介绍本文算法的基本概念;第4章介绍基于加权局部方差的改进K-means算法(weighted local variance K-means,WLV-K-means);第5章给出实验结果及分析比较;第6章为结束语。
2 相关工作
为克服传统K-means算法的这一不足,很多研究者对其进行不断改进。Katsavounidis等人[5]提出基于最大最小法的初始中心点选择方法。该方法首先选择具有最大欧几里德范数的对象作为第一个初始中心点,利用最大最小法逐个找到初始中心点。Wang[6]利用相异度矩阵构造哈夫曼树,从而选择K-means算法的初始中心点。Erisoglu等人[7]通过选择两个样本坐标的主轴,从而计算出样本在这两个主轴对应分量的均值。初始中心由两个主轴确定,第一个初始中心为到主轴均值距离最大的样本,第二个为主轴分量距离第一个初始中心距离最大的样本。后续聚类中心为与已经选中的初始中心距离之和最大的样本,重复该过程,直到获得指定个数的初始中心。Khan和Ahmad[8]提出了一种新的初始中心点方法(cluster center initialization algorithm,CCIA)。该方法通过对样本每一维分别进行聚类,发现K′(K′>K)类具有相同模式的点,分别得到K′类的中心点,再利用文献[9]的数据压缩方法,通过合并高密度样本的邻域,最终得到K个初始中心点。Rahman等人[10]提出了一种新的初始中心点选择技术DenClust。Den-Clust利用密度的方法,将距样本最小距离的样本数作为该样本的密度,进而选择高质量的初始种子集作为K-means算法的初始聚类中心。汪中等人[11]采用敏感的相似性度量来计算点的密度,找到K个初始中心,并以均衡化函数准则为标准,自动生成聚类数目。熊忠阳等人[12]提出了最大距离积法,根据密度参数找到高密度集合,分别找到两个聚类中心,搜索到聚类中心集合距离乘积最大的点作为下一个聚类中心,直到聚类中心的个数达到K。陈光平等人[13]提出了一种改进的初始中心点选择方法。该方法利用距离最大的两个样本作为初始的聚类中心,将剩余样本按距离划分。样本数较多的一簇,再找出相距最远的两个样本作为聚类中心,划分该簇。以此类推,直到找到K个聚类中心为止。曹永春等人[14]提出一种基于K-means的人工蜂群聚类算法,在每次迭代过程中,利用改进人工蜂群算法优化各聚类中心,分别对每个聚类中心进行K-means聚类。两个算法交替进行,直到聚类结束。文献[15-18]分别采用计算样本密度的不同方法,选择距离最远并且具有高密度的样本作为K-means算法的初始中心点。其中,文献[15]和[18]采用设定阈值的方式计算邻域密度,并选择相互距离最远的高密度区域作为初始中心点。文献[17]利用全局方差计算样本的邻域密度,选择方差小且相距一定距离的样本作为初始中心点。对K-means算法中的K值进行设定同样也是一个重要问题,孙镇江等人[19]提出了基于密度的循环首次适应K值优化算法。该算法通过设置密度阈值,将样本划分为多个簇集,从而确定K的个数。本文假设K已知。
3 基本概念
3.1 K-means算法
K-means算法的目的是为了使各簇中的样本到其簇中心的误差平方之和最小,算法首先从数据集D中随机选择K个样本,每个对象代表一个簇的初始中心点,分别计算D中剩余对象到各簇中心点的欧式距离,并将其分配到最相近的簇中,然后更新各簇的中心点,重新分配D中对象,迭代该过程直至收敛。K-means算法伪代码如下所示。
算法1 K-means算法
输入:聚类簇的数目K;包含n个对象的数据集D。输出:聚类结果集。
从D中任意选出K个对象作为初始中心点;
repeat
将每个对象划分到距离它最近的簇中心所在的簇中;重新计算每个簇中对象的均值,更新中心点;
until簇中点不再发生变化;
3.2样本方差
通过计算数据和期望之间的偏离程度得到方差,用于度量数据之间的离散程度,计算方法为求取各数据与期望之差的平方和的平均值,方差s2如式(1)所示:

其中,n为样本个数;xi为第i个样本;为样本均值,如式(2)所示:

方差越大,说明样本数据越分散,反之则说明越密集。在已知每个样本邻域的情况下,样本到其邻域内各样本距离的方差,能够反映出该样本邻域内密度的大小。
3.3最大最小法
最大最小法是文献[5]提出的初始聚类中心点选择方法,中心点的选择过程为:首先选择第一个中心点c1,然后计算数据集D中其他对象与c1之间的欧式距离,选择距离最大的对象作为下一个中心点c2。选择第i(i>2)个中心点ci时,计算数据集中剩余对象与之前中心点之间距离,将最近的欧式距离作为该对象的最大最小值,然后将最大最小值最大的对象作为下个中心点。重复该过程,直至选择出指定个数的初始中心点,如式(3)所示:
其中,mj为样本j的最大最小值;N为样本个数;mj如式(4)所示:

其中,ct为初始中心点集合T中的对象;d(ct,xj)为初始中心点ct与样本xj之间的欧式距离。
最大最小法可以找到相距较远的初始中心点,然而仅从距离判断,很有可能会将离群点作为初始中心点,从而导致K-means算法局部收敛。
4 W LV-K-means算法
4.1算法思想
在传统的K-means算法中,初始中心点选择的随机性,导致了聚类结果的不稳定性。由于中心点在迭代过程中不断更新,如果初始中心点选择不理想,会导致更新簇时,中心点偏离簇的真实值,从而最终收敛于局部最优解。因此中心点选择的主要问题是,除去噪声数据以及离群点,并发现分散且具有高密度邻域的初始点。
为度量样本邻域的密度,文献[11,18]通过设定参数调节样本的邻域半径,并计算邻域内样本数目作为邻域的密度。这类方法存在参数调节缺少客观性的问题。文献[16]将全部样本之间距离的平均值作为邻域半径,计算邻域内样本数作为邻域密度。该方法对各类分布均匀的样本效果较好,然而对于分布不均匀的样本,更应考虑局部的相关信息。文献[9]定义样本与距其第N近的样本之间距离作为该样本的密度,距离越小密度越大。然而该方法只考虑样本与距其第N近的样本之间的距离,而忽略与其他N-1个样本之间的距离。文献[17]通过计算样本到所有样本的距离方差,从而判断其邻域密度大小。然而对于邻域过于紧密或者过于稀疏的点均会被认为方差较大,将会忽略一些密集区域,影响聚类精度。
针对上述问题,本文提出了WLV-K-means算法,计算样本的邻域半径以及半径内样本至中心距离的方差,将加权局部方差作为新的密度度量标准。方差作为一种度量样本分布的概率统计量,可以客观地反映样本的离散程度。本文采用局部方差,一方面比计算全局变量的方法更具有适用性,另一方面方差的引入提高了密度计算的准确性。参数调节被映射到(0,1)范围内的子区间,因此更具客观性。局部方差的加权进一步提高了算法的抗噪能力。加权局部方差综合考虑样本分布问题及客观性等问题,将其作为密度度量标准更具合理性。
计算得到样本的加权局部方差后,对其排序,将最小值对应的样本作为第一个初始中心点。利用改进的最大最小法,在计算最大最小值时,将加权局部方差的倒数作为密度系数,对最大最小值加权,使得算法优先选择具有高密度的样本。逐个找出其他初始中心点,最终将初始中心点用到K-means算法中。
在改进的最大最小法中,密度系数的加入虽然提高了最大最小法的抗噪能力,但同时会增加算法的计算量,从而增加算法的时间复杂度。存储各样本的密度系数也会带来算法空间复杂度的增加。
4.2基本定义
对于一个数目为n的样本集(x1,x2,…,xn),每个样本xi为m维空间数据(xi1,xi2,…,xim)。
定义1样本xi的邻域半径ri如式(5)所示:
其中,D为样本集的距离矩阵;Di为样本xi到其他样本的距离按照从小到大排序后的行向量。因此Diëθ×n û表示样本xi到其他样本距离中第ëθ×n û近的距离,θ为邻域半径调节系数,取值范围为(0,1)。由上式可以得出,每个样本的邻域半径都是不同的,邻域半径小的样本处于高密度区域的可能性更大。
定义2样本xi的加权局部方差ρi如式(6)所示:
ρi=ωi×vi(6)
其中,vi为邻域半径内的局部方差;ωi为样本xi局部方差的权重。ρi越小,说明样本邻域内密度越大,vi和ωi如式(7)及式(8)所示:
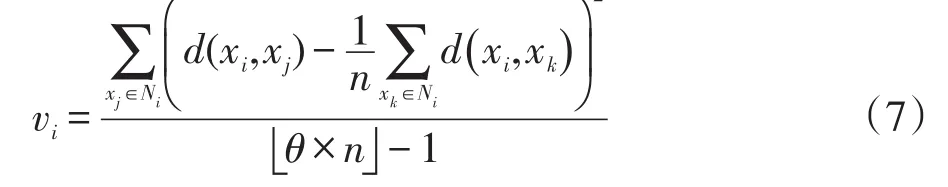
其中,Ni为样本xi邻域半径内的样本集合;d(xi,xj)表示样本xi与xj的欧式距离。
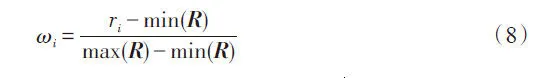
其中,R表示样本集的邻域半径向量,将样本xi的邻域半径ri归一化,使ωi∈[0,1]。
定义3加权最大最小值gi如式(9)所示:
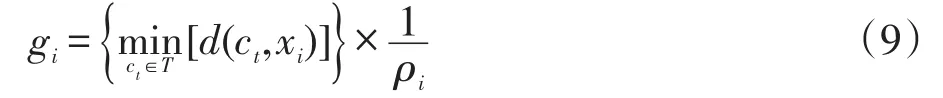
其中,T为初始中心点集合;ρi为式(6)求得的加权局部方差。样本xi的最大最小值gi为xi到中心点集中最近的距离乘以xi的加权局部方差的倒数1 ρi,加权局部方差越小,样本密度越大,则被选中的可能性越大。
4.3算法描述
算法中初始中心点选择主要分为两个阶段:第一个阶段是计算加权局部方差,判断样本的密度,并找出密度最大,即加权局部方差最小的样本。此过程中加入权值,能够进一步减小误选噪音点或者离群点的可能性。第二阶段为了防止所选中心点出现在同一类簇中,同样在最大最小法中利用密度加权,从而更有效地避免K-means算法中最终收敛于局部最优值。算法的伪代码如下所示。
算法2 WLV-K-means算法
输入:聚类簇的数目K;包含n个对象的数据集D;邻域半径调节参数θ。
输出:聚类结果集。
For D中的每个对象xi
根据式(5)计算xi的邻域半径ri;
将xi邻域半径内对象x′加入到集合Ni中;根据式(6)~(8)计算xi的加权局部方差ρi;end for
选择具有最小ρi的数据点p作为第一个初始中心点,加入集合T,并将p从D中删除;将p邻域内的对象从集合D中删除;while集合T中元素的个数小于K
for D每个对象x
根据式(9)计算x的加权最大最小值g;
end for
选择具有最大g对应的数据点p′作为下一个初
始中心点,加入集合T,并将p′从D中删除;
将p′邻域内的对象从集合D中删除;
end while
集合T作为初始中心点;
repeat
将数据集中对象划分到距其最近的中心点所在的簇中;
将各簇的均值作为更新的中心点;
until聚类的误差平方和不再发生变化;
4.4算法分析
传统K-means算法的时间复杂度为O(nKT),其中n为数据集中样本个数,K为簇数,T为迭代次数。本文提出的WLV-K-means算法由两部分组成,分别是计算加权局部方差以及利用改进最大最小法选择初始中心点。其中计算加权局部方差部分,由于需要计算样本间的距离矩阵,其时间复杂度为O(n2)。为计算距离样本第K近的距离,需对样本到其他样本距离进行排序,每个样本距其他样本距离的最优排序时间复杂度为O(n lb n),总的排序时间复杂度为O(n2lb n)。因此,计算加权局部方差的时间复杂度为O(n2(1+lb n))。利用改进最大最小法选择初始中心点部分的时间复杂度为O(K2n)。由于K,T≪n,算法整体的时间复杂度为O(n2(1+lb n)),空间复杂度为O(n2)。
为提高算法整体的效率,减少时间空间复杂度,可以将距第K近样本计算问题转化为K近邻查询,利用数据结构k-d树,计算距查询样本第K近的样本。从而减少计算距离矩阵的时间复杂度和存储距离矩阵的空间复杂度,进而降低算法整体的时间及空间复杂度。
5 实验分析
为验证WLV-K-means算法的聚类效果及稳定性,在UCI数据集上进行测试,并与传统K-means算法、文献[5]提出的算法Generalized Lloyd Iteration (GLI-K-means)、文献[11]提出的优化初始中心点的K-means算法(optim ized initial center points,OICP-K-means)、文献[15]提出的初始聚类中心优化的K-means算法(optim ization study on initial center,OS-K-means)以及文献[17]提出的最小方差优化初始聚类中心的K-means算法(m inimum deviation initialized clustering centers,MD-K-means)进行对比。
为更客观地对比,取100次实验的平均值作为传统K-means算法的聚类评价结果,其他几种对比算法的聚类结果,均取调参后的最佳结果。
实验结果的评价指标采用聚类准确率、聚类的误差平方和以及标准化互信息(normalized mutual information,NM I)[20]。
设样本集X包括k个类,聚类准确率的表示如式(10)所示:

其中,ai表示被正确划分到类Ci中的样本数;|| X表示样本总数。
聚类的误差平方和(sum of squared errors, SSE)的表示如式(11)所示:

其中,‖·‖为2-范数,C={ck,k=1,2,…,K}为K个簇集;xi为第k簇中的样本;μk为第k簇的簇中心。
NM I的表示如式(12)所示:
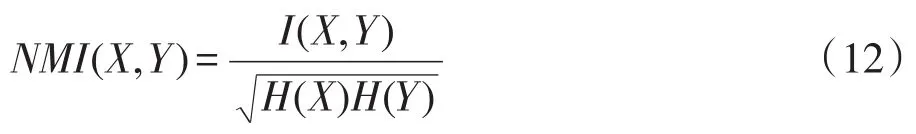
其中,X、Y为随机变量;I(X,Y)为X和Y之间的互信息;H(X)和H(Y)分别表示X和Y的熵,如式(13)~ (15)所示:
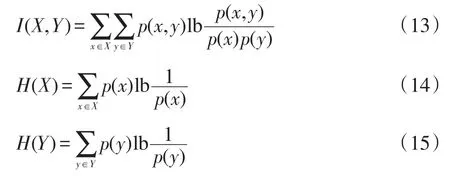
其中,p(x,y)为x和y的联合概率函数;p(x)和p(y)分别为x和y的概率函数。
5.1数据集描述
本文采用10个UCI数据库中聚类常用的数据集,如表1所示。
5.2实验结果及分析
实验的准确率、误差平方和以及NM I的对比结果如表2、表3和表4所示,其中加粗部分为最佳的聚类结果。
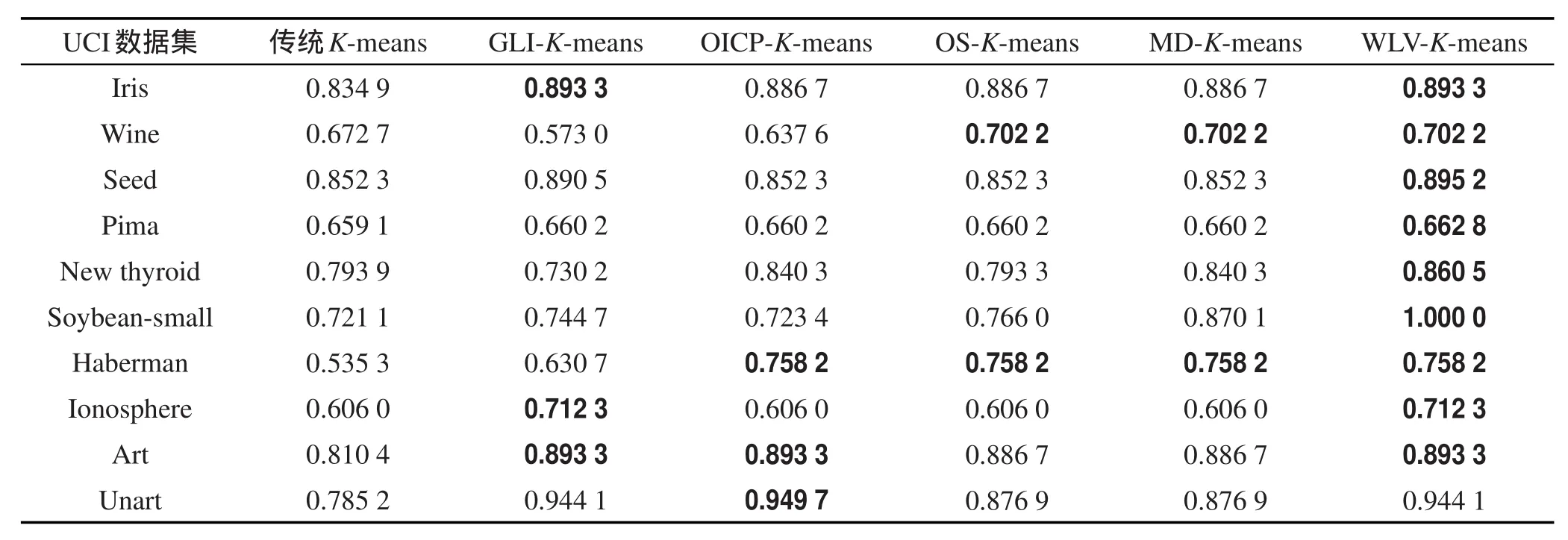
Table 2 Comparison of accuracy on UCI datasets between each algorithm表2 各算法在UCI数据集的准确率比较
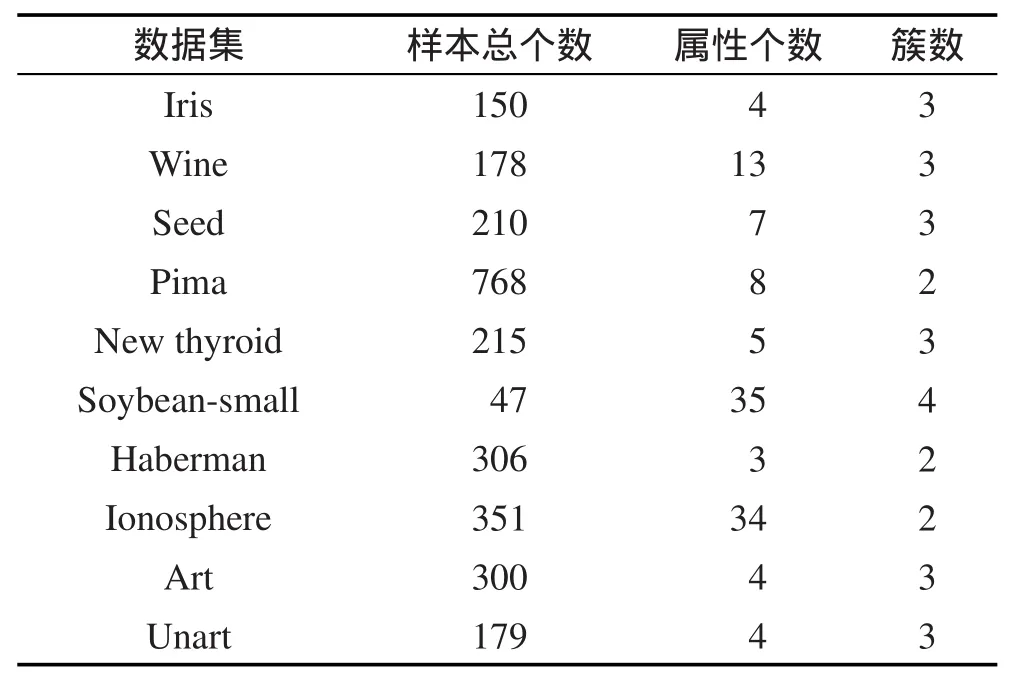
Table 1 Description of UCI datasets表1 UCI数据集描述
分析表2可以得出,WLV-K-means算法在Seed、Pima、New thyroid和Soybean-small数据集上的聚类准确率要高于其他5种算法,在Soybean-small数据集上的聚类准确率达到了100%。在Iris、seed和Ionosphere数据集上聚类准确率与GLI-K-means算法相同,高于其他4种算法。在W ine、Haberman和Art数据集上聚类准确率与其他对比算法的最大聚类准确率相等。
由表3误差平方和比较可以得出,WLV-K-means算法在Iris和Haberman数据集上的聚类误差平方和优于其他5种算法。在New thyroid,Soybean-small数据集上的误差平方和与MD-K-means算法相等,优于其他4种算法。在其他数据集上除Soybean-small、Unart及Ionosphere上聚类误差平方和略大于最优值,其他结果不差于传统K-means算法以及另外4种优化算法。
从表4中NM I的比较结果可以看出,WLV-K-means算法在除Unart数据集之外的其他UCI数据集上都有较好的聚类结果。
WLV-K-means算法对密度的计算以及中心点选取两个阶段进行改进。从实验结果可以得出,WLVK-means算法及对比算法在3种指标的比较中,在大多数数据集上都有较好的表现。
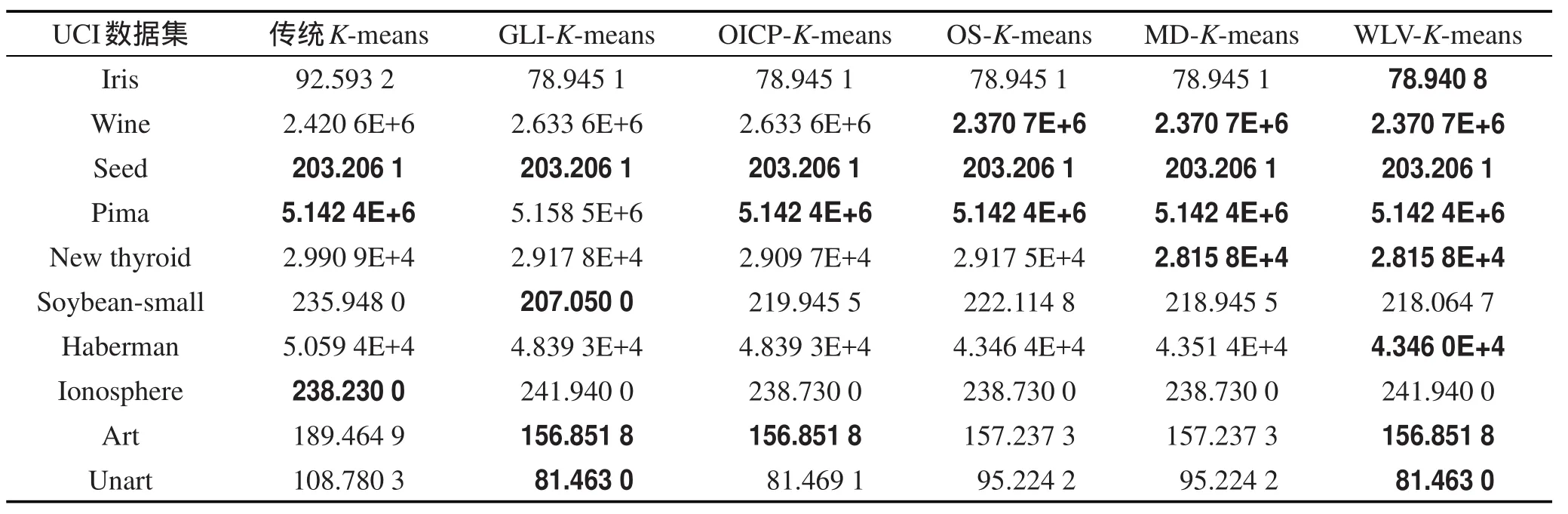
Table 3 Comparison of sum square error on UCI datasets between each algorithm表3 各算法在UCI数据集的误差平方和比较
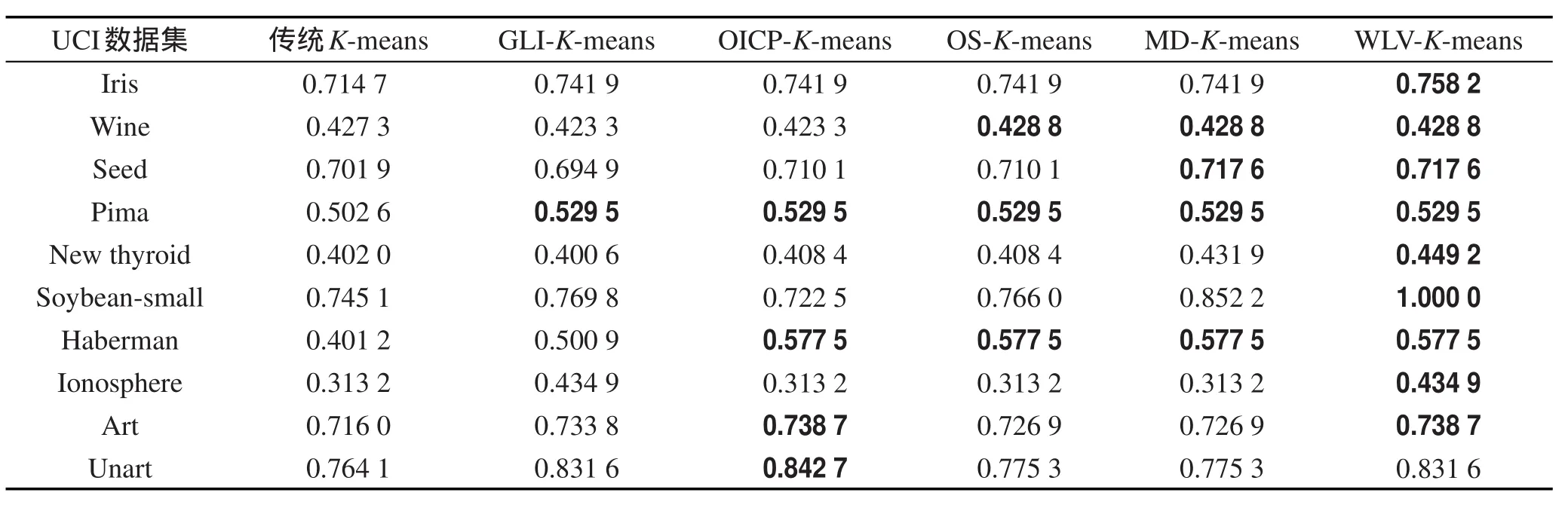
Table 4 Comparison of NM I on UCI datasets between each algorithm表4 各算法在UCI数据集的NM I比较
5.3参数调节
数据集中样本的数目及分布不同,WLV-K-means算法中最优半径调节参数θ也相应不同。半径调节参数θ取值范围为(0,1),而且其取值与数据集的个数N以及簇数K有关。对各类数据个数接近N/ K的数据集,最理想状态为样本邻域内样本数为N/ K,此时合适的中心点可以分别表示各个类簇。为了防止不同数据集中存在一定的偏差,将θ的取值范围设置为[N/ K -0.15,N/ K]。对于各类数据比例相差较大的数据集,如果取θ接近N/ K,个数较少类中的样本会被忽略。因此θ将从最小值开始逐步递增,取值范围为[0.01,0.15]。在两种取值范围内,以0.01为步长,在UCI数据集上,不同参数对应的聚类准确率如图1所示。
从图1中可以得出,各数据集在对应的区间中均能找到最优准确率。第一类数据集在N/ K处,准确率达到收敛状态。第二类数据集中,当θ取较小值时的聚类效果要优于其取较大值的聚类效果。聚类准确率在参数变化区间内的变动幅度较小,说明本文算法的稳定性更好,不会出现由于参数选择不合适而导致聚类结果过大的变化。
数据集Soybean-small的实验中,当θ取值较小时,聚类效果更理想。在计算样本的加权局部方差时,样本的邻域半径依赖于θ。由于数据集Soybeansmall的数据量较小且各类数据量分布不均匀,当θ取较小值时才能保证样本的邻域半径处于较小范围内,从而更好地发现分布密集的区域,并且能够找到样本数较少的类的中心点。如果θ取值过大,会导致邻域半径过大,一方面使得样本邻域半径内部包含其他类的样本或者噪声数据,另一方面在利用加权最大最小法选择中心时会将样本数较少的类忽略,从而不能准确地发现各类的初始中心点。
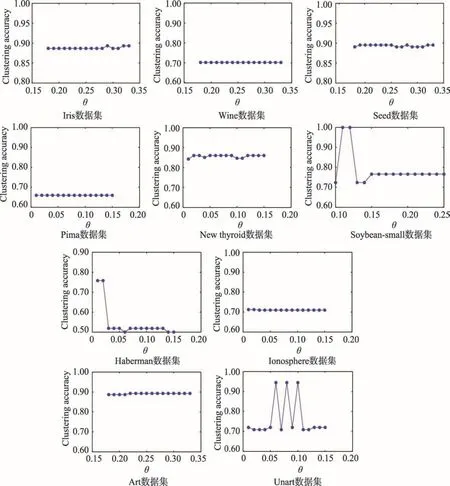
Fig.1 Variation trend of clustering accuracy on UCI datasets w ith the change of parameter图1 UCI数据集聚类准确率随参数变化趋势
6 结束语
传统K-means算法过程中,初始中心点选择的随机性,使得聚类结果不稳定,并且容易使聚类结果达到局部最优,难以得到理想的聚类结果。而已有的基于密度选择中心点的优化算法,算法的聚类效果过度依赖阈值的设定,具有一定的局限性。本文提出了一种基于加权局部方差的密度计算方法,并利用改进的最大最小法,启发式地选择初始中心点。在UCI数据集上的实验结果证明了本文算法提高了聚类的质量,具有较好的稳定性。
References:
[1] Han Jiawei, Kamber M, Pei Jian. Data mining concepts and techniques[M]. 3rd ed. Fan M ing, Meng Xiaofeng. Beijing: China Machine Press, 2012: 288-290.
[2] Jain A K. Data clustering: 50 years beyond K-means[J]. Pattern Recognition Letters, 2010, 31(8): 651-666.
[3] Sun Jigui, Liu Jie, Zhao Lianyu. Clustering algorithm research[J]. Journal of Software, 2008, 19(1): 48-61.
[4] Celebi M E, Kingravi H A, Vela P A. A comparative study of efficient initialization methods for the K-means clustering algorithm[J]. Expert Systems w ith Applications, 2012, 40 (1): 200-210.
[5] Katsavounidis I, Jay Kuo C C, Zhang Zhen. A new initialization technique for generalized Lloyd iteration[J]. Signal Processing Letters, 1994, 1(10): 144-146.
[6] Wang Shunye. An improved k-means clustering algorithm based on dissim ilarity[C]//Proceedings of the 2013 International Conference on Mechatronic Sciences, Electric Engineering and Computer, Shengyang, China, Dec 20-22, 2013. Piscataway, USA: IEEE, 2013: 2629-2633.
[7] Erisoglu M, Calis N, Sakallioglu S. A new algorithm for initial cluster centers in k-means algorithm[J]. Pattern Recognition Letters, 2011, 32(14): 1701-1705.
[8] Khan S S, Ahmad A. Cluster center initialization algorithm for K-means clustering[J]. Pattern Recognition Letters, 2004, 25(11): 1293-1302.
[9] Mitra P, Murthy C A, Pal S K. Density-based multiscale data condensation[J]. IEEE Transactions on Pattern Analysis and Machine Intelligence, 2002, 24(6): 734-747.
[10] Rahman M A, Islam M Z, Bossomaier T. DenClust: a density based seed selection approach for K-means[C]//LNCS 8468: Proceedings of the 13th International Conference on Artificial Intelligence and Soft Computing, Zakopane, Poland, Jun 1-5, 2014. [S.l.]: Springer International Publishing, 2014: 784-795.
[11] Wang Zhong, Liu Guiquan, Chen Enhong. A K-means algorithm based on optim ized initial center points[J]. Pattern Recognition and Artificial Intelligence, 2009, 22(2): 299-304. [12] Xiong Zhongyang, Chen Ruotian, Zhang Yufang. Effective method for cluster centerƳs initialization in K-means clustering[J]. Application Research of Computers, 2011, 28 (11): 4188-4190.
[13] Chen Guangping, Wang Wenpeng, Huang Jun. Improved initial clustering center selection method for K-means algorithm[J]. Journal of Chinese Computer Systems, 2012, 33 (6): 1320-1323.
[14] Cao Yongchun, Cai Zhengqi, Shao Yabin. Improved artificial bee colony clustering algorithm based on K-means[J]. Journal of Computer Applications, 2014, 34(1): 204-207.
[15] Lai Yuxia, Liu Jianping. Optim ization study on initial center of K-means algorithm[J]. Computer Engineering and Applications, 2008, 44(10): 147-149.
[16] Han Lingbo, Wang Qiang, Jiang Zhengfeng, et al. Improved K-means initial clustering center selection algorithm[J]. Computer Engineering and Applications, 2010, 46(17): 150-152.
[17] Xie Juanying, Wang Yan Ƴe. K-means algorithm based on minimum deviation initialized clustering centers[J]. Computer Engineering, 2014, 40(8): 205-211.
[18] Fu Desheng, Zhou Chen. Improved K-means algorithm and its implementation based on density[J]. Journal of Computer Applications, 2011, 31(2): 432-434.
[19] Sun Zhenjiang, Liang Yongquan, Fan Jiancong. Optimization study and application on the K value of K-means algorithm[J]. Journal of Bioinformatics and Intelligent Control, 2013, 2(3): 223-227.
[20] Fan Jiancong. OPE-HCA: an optimal probabilistic estimation approach for hierarchical clustering algorithm[J]. Neural Computing and Applications, 2015.
附中文参考文献:
[1] Han Jiawei, Kamber M,Pei Jian.数据挖掘概念与技术[M].范明,孟小峰. 3版.北京:机械工业出版社, 2012: 288-290.
[3]孙吉贵,刘杰,赵连宇.聚类算法研究[J].软件学报, 2008, 19(1): 48-61.
[11]汪中,刘贵全,陈恩红.一种优化初始中心点的K-means算法[J].模式识别与人工智能, 2009, 22(2): 299-304.
[12]熊忠阳,陈若田,张玉芳.一种有效的K-means聚类中心初始化方法[J].计算机应用研究, 2011, 28(11): 4188-4190.
[13]陈光平,王文鹏,黄俊.一种改进初始聚类中心选择的K-means算法[J].小型微型计算机系统, 2012, 33(6): 1320-1323.
[14]曹永春,蔡正琦,邵亚斌.基于K-means的改进人工蜂群聚类算法[J].计算机应用, 2014, 34(1): 204-207.
[15]赖玉霞,刘建平. K-means算法的初始聚类中心的优化[J].计算机工程与应用, 2008, 44(10): 147-149.
[16]韩凌波,王强,蒋正锋,等.一种改进的K-means初始聚类中心选取算法[J].计算机工程与应用,2010,46(17):150-152.
[17]谢娟英,王艳娥.最小方差优化初始聚类中心的K-means算法[J].计算机工程, 2014, 40(8): 205-211.
[18]傅德胜,周辰.基于密度的改进K均值算法及实现[J].计算机应用, 2011, 31(2): 432-434.

CAI Yuhao was born in 1990. He is an M.S. candidate at College of Information Science and Engineering, Shandong University of Science and Technology. His research interests include machine learning and data m ining, etc.
蔡宇浩(1990—),男,山东青州人,山东科技大学信息科学与工程学院硕士研究生,主要研究领域为机器学习,数据挖掘等。

LIANG Yongquan was born in 1968. He is a professor at College of Information Science and Engineering, Shandong University of Science and Technology, and the senior member of CCF. His research interests include machine learning, data mining, distributed artificial intelligence and intelligent multimedia information processing, etc.
梁永全(1968—),男,山东聊城人,博士,山东科技大学信息科学与工程学院教授,CCF高级会员,主要研究领域为机器学习,数据挖掘,分布式人工智能,多媒体信息智能处理等。

FAN Jiancong was born in 1977. He is an associate professor at College of Information Science and Engineering, Shandong University of Science and Technology, and the member of CCF. His research interests include machine learning, data m ining, evolutionary computation and mass data processing, etc.
樊建聪(1977—),男,山东青岛人,博士,山东科技大学信息科学与工程学院副教授,CCF会员,主要研究领域为机器学习,数据挖掘,演化计算,海量信息处理等。

LI Xuan was born in 1993. She is an M.S. candidate at College of Information Science and Engineering, Shandong University of Science and Technology. Her research interests include machine learning and data m ining, etc.
李璇(1993—),女,山东宁阳人,山东科技大学信息科学与工程学院硕士研究生,主要研究领域为机器学习,数据挖掘等。

LIU Wenhua was born in 1990. She is an M.S. candidate at College of Information Science and Engineering, Shandong University of Science and Technology. Her research interests include machine learning and data mining, etc.
刘文华(1990—),女,山东烟台人,山东科技大学信息科学与工程学院硕士研究生,主要研究领域为机器学习,数据挖掘等。
Optim izing Initial Cluster Centroidsby Weighted Local Variance in K-means Algorithmƽ
CAI Yuhao, LIANG Yongquan, FAN Jiancong+, LI Xuan, LIU Wenhua
College of Information Science and Engineering, Shandong University of Science and Technology, Qingdao, Shandong 266590, China
+ Corresponding author: E-mail: fanjiancong@sdust.edu.cn
Key words:K-means algorithm; variance; weighting; max-m in method; initial cluster centroids
Abstract:The selection of initial cluster centroids in the classical K-means algorithm is random, which causes that the clustering results vary w ith different selections of cluster centroids. Thereby many selection approaches of initial centroids are devised and applied. However, most of them are affected by parameters design and parameter values. To overcome this problem, this paper proposes a novel initial cluster centroids selection algorithm, called WLV-K-means (weighted local variance K-means). The WLV-K-means algorithm employs the weighted local variance to measure the density of each sample, which can find samples w ith higher density. This algorithm also uses the improved max-min method to select cluster centroid heuristically. The experiments are made on UCI datasets and the results show that the WLV-K-means algorithm outperforms some improved K-means algorithms and is more stable and robust.
doi:10.3778/j.issn.1673-9418.1509024 E-mail: fcst@vip.163.com
文献标志码:A
中图分类号:TP181

