利用图形旋转变换解题的思路探索

张建能

摘 要：这一轮课程改革，对几何作了较大幅度的调整，印象较深之一是加强了“几何变换”的内容，即从变换的角度去认识传统几何中的证题术。初中几何涉及的变换主要有平移、对称和旋转，本文从“旋转”这一角度举些例子，供大家参考。

关键词：数学；旋转；解题

中图分类号：G632 文献标识码：B 文章编号：1002-7661（2016）11-319-01

例1、如图〔1〕分别以正方形ABCD的边AB、AD为直径画半圆，若正方形的边长为 ，求阴影部分的面积。

解：连AC、BD如右图，则绕AD中点将图中②逆时针旋转 到图中③，将图中①绕AB中点顺时针方向旋转 到图中④，则原图中阴影部分的面积就和△DBC的面积相等，所以图中阴影部分的面积=S⊿DCB = S 正方形ABCD= 。这里我们用旋转变换的方法改变了图中①和②的位置，从而顺利地完成了计算。

例2、如图⑵所示，在⊿ABC中，AB=AC，∠BAC= ，D是BC上任一点，试说明 。

证法一（非旋转法）：过A点作

AE⊥BC于E，如图⑶，则容易证明AE=BE=EC，又BD=BE-DE，DC=CE+DE，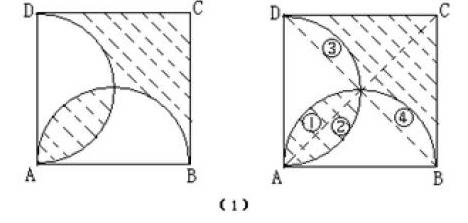

所以 ， ，所以 = + = ，而在直角三角形ADE中，存在 ，所以 ，这是传统的证明方法。

本题考虑到BD、DC、AD三线段分散在两个三角形中，而且构成平方和的条件不明显，若利用旋转变换，将BD、DC放到一个三角形中，若这个三角形是直角三角形，则创造 就更能接近所证的目标了。

证法二（旋转法）： 将△ADC绕A点顺时针方向旋转 到△AEB，如图⑷， 连DE， 易知△ADE、△DBE均为直角三角形，且AE=AD，BE=DC， 所以在Rt△EBD中有 ，在Rt△AED中有 ，所以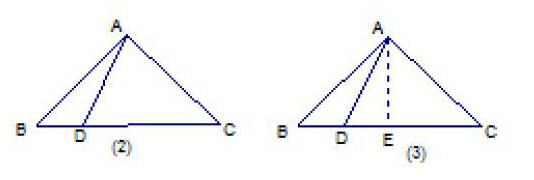

例3、如图⑸所示，P为正方形内一点，且PA=1，BP=2，PC=3，求∠APB的大小

解： 如图（6），将⊿BPC绕B点逆时针旋转 到△BEA， 连EP易知∠PBE= 且AE=PC=3 BE=BP=2，在Rt⊿BEP中， ， 且∠EPB= ，在⊿AEP中 ，又 ，所以△APE是直角三角形，即∠APE= ，∠APB=∠APE+∠EPB= + = ，即∠APB为

传统几何中，有许多旋转的例子，尤其是正方形和等腰三角形中。如图（7），正方形ABCD的边长为1，AB、AD上各有一点P、Q，如果△APQ的周长为2，求∠PCQ的度数。

将△CDQ绕C点逆时针旋转90°像图（8）那样，立刻可得QA+AB+BE=2，由△APQ周长为2得 PQ=PE，进一步可得△CPQ≌△CPE，∠PCQ=∠PCE，又∠QCE=90°，所以∠PCQ=45°

又如图（9），△ABC中，AB=AC，P为三角形内一点，且∠APB>∠APC，求证：PC>PB。将△APB绕A点逆时针旋转成右图那样，不难得到条件∠APB>∠APC变成了∠PQC>∠QPC，从而PC>CQ，由旋转关系，PC>PB。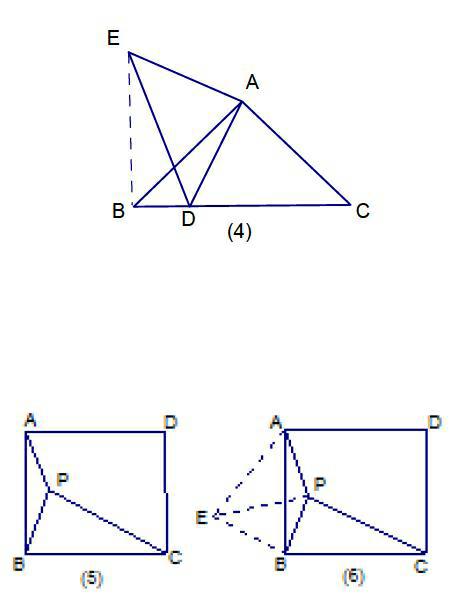

最能体现旋转法的莫过于下面这个问题了：如图（10），四边形ABCD中，AB=AD，∠A=∠C=90°，其面积为16，求A到BC的距离。通过旋转变换，将图（10）变成图（11），答案可以脱口而出：距离为4！类似的例子可以举出许多，这里不再赘述。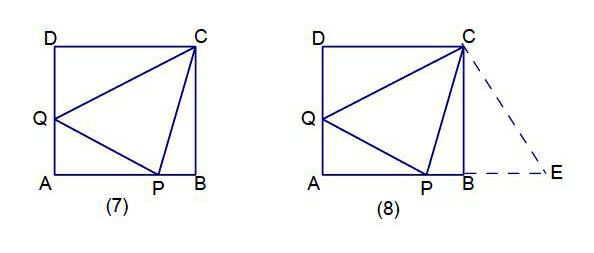

综上可见，正确利用图形的旋转变换可大大提高解题效率，不过在使用这一方法解题时还需注意图形旋转变换的基础，即存在相等的线段，故这种方法一般常用于等腰三角形，正方形图形中。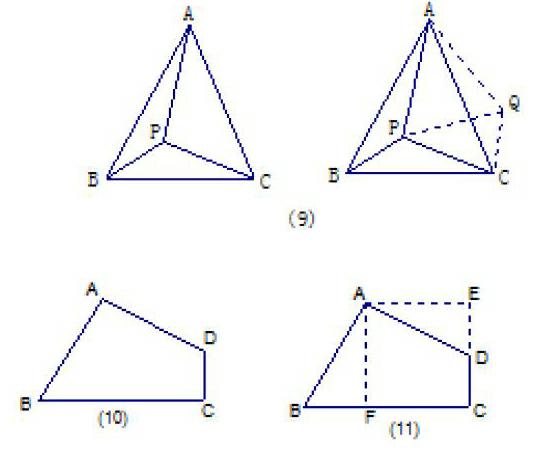

参考文献：

[1] 吴秀明.加强基本图形研究，有效实施初中数学图形归纳[J].数理化学习：初中版，2015（3）.

[2] 桑高峰.浅析初中数学图形类问题教学[J].中学时代，2014（16）