空间中特定自仿测度的谱性质分析

李　敏

(陕西师范大学 数学与信息科学学院,陕西 西安 710062)



空间中特定自仿测度的谱性质分析

李敏

(陕西师范大学 数学与信息科学学院,陕西 西安 710062)

摘要:在三维空间R3中，当M=1/2[p1+p2,p1-p3,p2-p3;p1-p2,p1+p3,-p2+p3;-p1+p2,-p1+p3,p2+p3],D={0,e1,e2,e3}时,其中pj∈Z{0,±1}(j=1,2,3),e1,e2,e3是R3中的单位向量,对迭代函数系{φd(x)}d∈D产生的自仿测度μM,D的谱性质进行分析.得到:(1)当pj∈2Z{0,2}(j=1,2,3)或p1=p2=p3=2时,μM,D是谱测度;(2)当p1,p2,p3至少有一个数是偶数时,空间L2(μM,D)中存在无限正交系E(Λ)且Λ⊆Z3;(3)当pj∈2Z+1{±1}(j=1,2,3)时,μM,D不是谱测度,且空间L2(μM,D)中正交指数函数系至多包含4个元素,且数字“4”是最好的.

关键词:谱测度;正交指数函数系;数字集

1引言及主要结论

设M∈Mn(Z)为n阶整数扩张矩阵,D⊂Zn为有限数字集且基数为|D|.由仿射变换组成的迭代函数系{φd(x)=M-1(x+d)}d∈D产生的自仿测度μ:=μM，D是满足等式

(1)

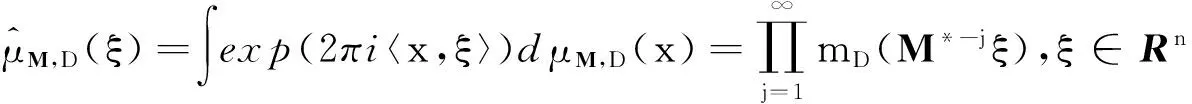
(2)

这里M*表示M的共轭转置矩阵(实际上,M*=Mt)，且

(3)

关于自仿测度的谱与非谱问题还有以下两个猜测:

猜测1[10]设M∈Mn(Z)为扩张矩阵,D⊂Zn为有限数字集且0∈D,如果存在S⊂Zn,0∈S,使得(M-1D,S)为和谐对,则μM，D是谱测度.

猜测2[11]设M∈Mn(Z)为扩张矩阵,D⊂Zn为有限数字集,如果|D|∉W(m),这里W(m)是|det(M)|=m的素数因子的非负整数组合,则μM，D不是谱测度,且空间L2(μM，D)中正交指数函数系至多有有限个.

猜测1和猜测2只能在一定条件下证明其成立[7，10-12]，对于一般情况下是否成立还有待进一步的研究.对于上述M,D,S,由迭代函数系{Ψs(x)=M*-1(x+s)}s∈S产生的吸引子为T:=T(M*,S),且

(4)

自仿测度的谱与非谱问题主要在平面上进行讨论,而且结论比较完善[13].而空间上仅对M是对角矩阵或上三角矩阵讨论过[14].对M是任意的三阶矩阵还有一定的难度与复杂性.本文在此基础上,对特殊的三阶矩阵进行讨论,推广文献[14]的结论并得到如下定理.

定理1对于如下形式的扩张矩阵和数字集

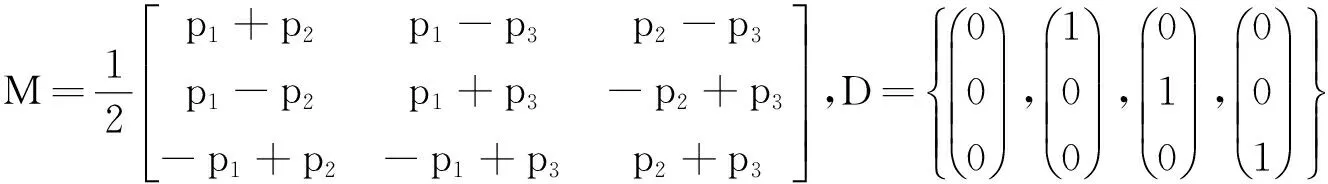
(5)

其中pj∈Z{0,±1}(j=1,2,3),下列结论成立:

(1)当pj∈2Z{0,2}(j=1,2,3)或p1=p2=p3=2时,μM，D是谱测度;

(2)当p1,p2,p3中至少有一个数是偶数时,空间L2(μM，D)中存在无限正交系E(Λ)且Λ⊆Z3;

(3)当pj∈2Z+1{±1}(j=1,2,3)时,μM，D不是谱测度,且空间L2(μM，D)中正交指数函数系至多包含4个元素,且数字“4”是最好的.

2定理1的证明

设M∈Mn(Z)为n阶整数扩张矩阵,D⊂Zn为有限数字集，且0∈D.若存在S⊂Zn为有限子集且0∈S,使得(M-1D,S)为和谐对,则由共轭迭代函数系{φs(x)=M*x+s}s∈S产生的不变子集为Λ(M,S),且M*Λ(M,S)+S=Λ(M,S).当用Λ(M,S)表示0在迭代函数系{φs(x)}s∈S下的扩张轨迹时,

(6)

E(Λ(M,S))是空间L2(μM，D)的无限正交系,但不一定是空间L2(μM，D)的正交基[15].为了确保E(Λ(M,S))在空间L2(μM，D)中的完备性,Strichartz[5]得到如下定理.

定理A设M∈Mn(Z)为扩张矩阵,D,S⊂Zn为有限子集,使得(M-1D,S)为和谐对且0∈D∩S.假设函数mM-1D(x)的零点集Z(mM-1D(x))与T(M*,S)不相交,则Λ(M,S)是μM，D的谱.

该定理也是证明μM，D为谱测度的常用方法，对于形如式(5)中的M和D，令

从而有

(7)

由相似变换不改变自仿测度的谱性质可知,μM，D与μM0,D0的谱性质相同.因此可以通过证明μM0,D0的谱性质,来得到μM，D的谱性质,即得到定理1的证明.

定理2对于式(7)中的整数扩张矩阵M0和数字集D0,有下列结论成立:

(1)当pj∈2Z{0,2}(j=1,2,3)或p1=p2=p3=2时,μM0,D0是谱测度;

(2)当p1,p2,p3中至少有一个数是偶数时,空间L2(μM0,D0)中存在无限正交系E(Λ0)且Λ0⊆Z3;

(3)当pj∈2Z+1{±1}(j=1,2,3)时,μM0,D0不是谱测度,且空间L2(μM0,D0)中正交指数函数系至多包含4个元素,且数字“4”是最好的.

证明(1)证明当pj∈2Z{0,2}(j=1,2,3)时，μM0,D0是谱测度.令

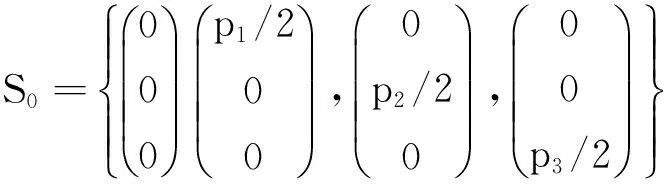
(8)

(9)

(10)

(11)

对于式(7)中的数字集D0,由

x=(x1,x2,x3)t∈R3.

(12)

可得

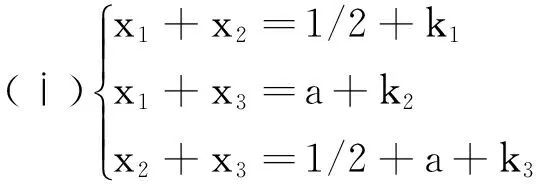
(13)

其中k1,k2,k3∈Z,a∈R.解式(13)可得

(14)

其中k1,k2,k3∈Z,a∈R.化简式(14)即可得式(12)的解为A1∪A2…∪A6,其中:

(15)

由式(12)和(15)可得

Z(mD0(x))={x∈R3:mD0(x)=0}=A1∪A2…∪A6.

(16)

(17)

又因为

(18)

(19)

由式(11)和(19),以及定理A可知,对于式(8)中的S0⊂Z3,Λ0(M0,S0)是μM0,D0的谱.即μM0,D0是谱测度且谱为Λ0(M0,S0).

其次,当p1=p2=p3=2时,由文献[16]可知μM0,D0的谱测度.综上证明可知结论(1)成立.

(2)当p1,p2,p3中至少有一个数是偶数时,设p1∈2Z{0}.因为

且M0α1∈Z3,则由文献[17]的定理2可知,空间L2(μM0,D0)中存在无限正交系E(Λ0)且Λ0⊆Z3.同理可证其他情形,故该结论成立.

(3)由式(16)可知，

Θ0:=Z(mD0(x))=A1∪A2…∪A6,

(20)

令

(21)

再令B=R(Z∪(1/2+Z)).则

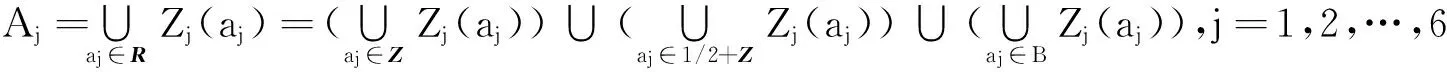
(22)

由式(21),经过计算可知

(23)

记

(24)

由式(20)～(24),可得

(25)

因为pj∈2Z+1{±1}(j=1,2,3)，所以计算可得

(26)

(27)

其中

(28)

计算可得以下引理.

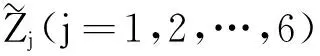
(h) Z1-Z3=Z6,Z1-Z4=Z5,Z1-Z5=Z4,Z1-Z6=Z3,Z2-Z3=Z5,Z2-Z4=Z6,Z2-Z5=Z3,Z2-Z6=Z4,Z3-Z5=Z2,Z3-Z6=Z1，Z4-Z5=Z1,Z4-Z6=Z2;

假设λ1，λ2,…,λ5∈R3是使得下面的5个指数函数

exp(2πi〈λ1,x〉),exp(2πi〈λ2,x〉),exp(2πi〈λ3,x〉),exp(2πi〈λ4,x〉),exp(2πi〈λ5,x〉)

(29)

由式(27)和(29)可知，下面的10个差

(30)

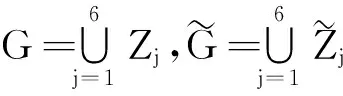
(31)

则

(32)

结合式(31)分以下几个情形证明该定理.

通过下面的步骤1,2,3说明情形1,2,3均不成立,即可证得定理2(3).

步骤1集合G至多包含式(32)中的3个差.

证明首先证明Zj(j=1,2,…,6)至多包含式(32)中的一个差.假设存在某个j∈{1,2,…,6},使得Zj包含式(32)中的2个差,设λ2-λ1,λ3-λ1∈Z1,则由引理1(c)可知

λ3-λ2=(λ3-λ1)-(λ2-λ1)∈Z1-Z1⊆Z3,

再由引理1(b)及式(29)即可推出矛盾.

其次证明Zj与Zj+1(j=1,3,5)不能同时包含式(32)中的差.假设Z1与Z2包含式(32)中的差,设λ3-λ1∈Z1,λ2-λ1∈Z2,则

λ3-λ2=(λ3-λ1)-(λ2-λ1)∈Z1-Z2,

由引理1(f)及式(29)即可推出矛盾.

由以上分析可知,集合G至多包含式(32)中的3个差.

(33)

(34)

由式(33),(34)以及引理1(c)可知

λ3-λ2=(λ4-λ2)-(λ4-λ3)∈Z5-Z5⊆Z3,

再由引理1(b)及式(29)即可推出矛盾.

由引理1(e)及式(29)即可推出矛盾.

由引理1(e)可知

(35)

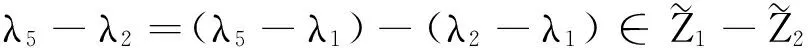
(36)

结合引理1(c)以及式(35)，(36)，可得

λ3-λ2=(λ5-λ2)-(λ5-λ3)∈Z6-Z6⊆Z3,

步骤3结合步骤1,2以及式(32),分下面两种情形证明该定理:

并且这两种情形均不可能成立.

综上证明可知,当pj∈2Z+1{±1}(j=1,2,3)时,μM0,D0不是谱测度,且空间L2(μM0,D0)中至多有4个正交指数函数系.而且可以找到4个正交指数函数系,如对式(8)中的S0,指数函数系E(S0)就是空间L2(μM0,D0)正交系.从而可知数字“4”是最好的.

根据相似变换不改变谱性质以及定理2,即可得到定理1的结论.

例1对如下形式的扩张矩阵和数字集

则空间L2(μM，D)中存在无限正交系E(Λ)且Λ⊆Z3.

证明因为

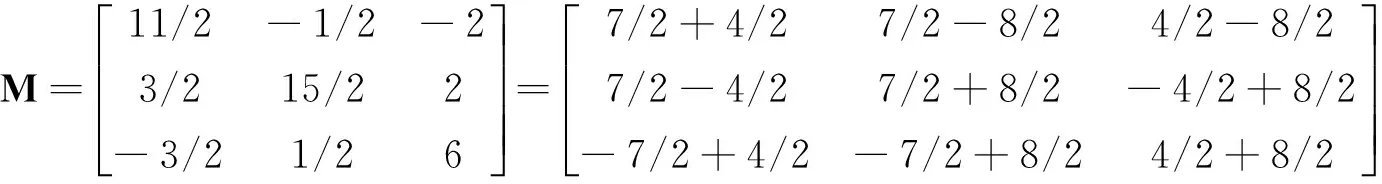
故可作相似变换,令

从而有

由定理2可知,空间L2(μ(M0,D0))中存在无限正交系E(Λ0)且Λ0⊆Z3,从而空间L2(μM，D)中存在无限正交系E(Λ)且Λ⊆Z3.

参考文献:

[1]FUGLEDEB.Commutingself-adjointpartialdifferentialoperatorsandagrouptheoreticproblem[J].JFunctAnal,1974,16(1):101-121.

[2]JORGENSENPET,PEDERSENS.DenseanalyticsubspacesinfractalL2-spaces[J].JAnalMath,1998,75(1):185-228.

[3]张陇生.自仿测度的谱性质[J]. 纺织高校基础科学学报 ,2009，22(4) ：445-448.

ZHANGLongsheng．Spectralpropertiesofself-affinemeasure[J]．BasicSciencesJournalofTextileUniversities,2009，22(4) ：445-448.

[4]高桂宝.R3中共线数字集自仿测度的谱性质[J].吉林大学学报:理学版,2014，52(2):2-6.

GAOGuibao.Spectralityofself-affinemeasureswithcollineardigitsetonR3[J].JournalofJilinUniversity:ScienceEdition,2014,52(2):2-6.

[5]STRICHARTZR.Remarkson"DenseanalyticsubspacesinfractalL2-spaces"[J].JAnalMath,1998,75(1):229-231.

[6]STRICHARTZR.MockFourierseriesandtransformsassociatedwithcertainCantormeasures[J].JAnalMath,2000,81(1):209-238.

[7]LABAI,WANGYang.OnspectralCantormeasures[J].JFunctAnal,2002,193(2):409-420.

[8]DUTKAYDE,JORGENSENPET.Dualityquestionsforoperatorsspectrumandmeasures[J].ActaApplMath,2009,108(3):515-528.

[9]张陇生.一类三元素数字集的平面自仿测度的非谱性质[J].山东大学学报:理学版,2011,46(2):5-8.

ZHANGLongsheng.Non-spectralityofaclassofplanarself-affinemeasureswiththree-elementdigitset[J].JournalofShandongUniversity:NaturalScience,2011,46(2):5-8.

[10]DUTKAYDE,JORGENSENPET.Fourierfrequenciesinaffineiteratedfunctionsystems[J].JFunctAnal,2007,247(1):110-137.

[11]LIJianlin.Non-spectralproblemforaclassofplanarself-affinemeasures[J].JFunctAnal,2008,255(11):3125-3148.

[12]LIJianlin.Spectralself-affinemeasuresinRn[J].Pro Edinburgh Math Soc,2007,50 (1):197-215.

[13]LI Jianlin,WEN Zhiying.Spectrality of planar self-affine measures with two-element digit set[J].Sci China Math,2012,55(3):593-605.

[14]LI Jianlin.Spectrality of self-affine measures on the three-dimensional Sierpinski gasket[J].Pro Edinburgh Math Soc,2012,55(3):477-496.

[15]JORGENSEN P E T,PEDERSEN S.Harmonic analysis of fractal measures[J].Constr Approx,1996,12(1):1-30.

[16]DUTKAY D E,JORGENSEN P E T.Analysis of orthogonality and of orbits inaffine iterated function systems[J].Math Z,2007,256(4):801-823.

[17]LI Jianlin.On the μM，D-orthogonal exponentials[J].Nonlinear Analysis,2010,73(4):940-951.

编辑：武晖；校对：师琅

文章编号:1006-8341(2016)02-0152-09

DOI：10.13338/j.issn.1006-8341.2016.02.004

收稿日期:2015-03-15

作者简介:李敏(1989—),女,河南省焦作市人,陕西师范大学硕士研究生,研究方向为谱自仿测度理论. E-mail:limin.good@snnu.edu.cn

中图分类号：O 174.2

文献标识码：A

Analysis of spectral for the certain spatial self-affine measure

LIMin

(College of Mathematics and Information Science, Shaanxi Normal University, Xi′an 710062，China)

Abstract:The spectrality of the affine-measures μM,Dproduced from iterated function system {φd(x)}d∈Dis analyzed when M=1/2[p1+p2, p1-p3, p2-p3; p1-p2, p1+p3,-p2+p3;-p1+p2,-p1+p3, p2+p3], D={0, e1,e2,e3} are in the space R3, where pj∈ Z{0,±1}(j=1,2,3), e1, e2, e3 are the standard basis of unit column vectors in R3.It is obtained that (1) if pj∈ 2Z{0, 2}(j=1,2,3) or p1=p2=p3=2, then μM,Dis a spectral measure; (2) if there is at least one even number among p1, p2, p3, then there are infinite families of orthogonal exponentials E(Λ) and Λ⊆Z3;(3)if pj∈ 2Z+1{±1}(j=1,2,3), then μM,Dis a non-spectral measure, and there exist at most 4 mutually orthogonal exponential functions in L2(μM,D), where the number 4 is the best.

Key words:spectral measures;orthogonal exponentials;digital set

引文格式：李敏.空间中特定自仿测度的谱性质分析[J].纺织高校基础科学学报,2016,29(2)：152-160.

LI Min.Analysis of spectral for the certain spatial self-affine measure[J].Basic Sciences Journal of Textile Universities,2016,29(2):152-160.