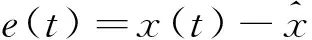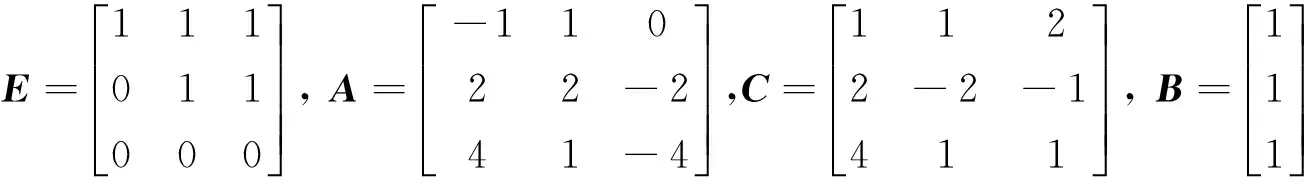分数阶不确定奇异系统的镇定

李路路,吴保卫,曹　晔,马亚静

(陕西师范大学 数学与信息科学学院,陕西 西安 710062)



分数阶不确定奇异系统的镇定

李路路,吴保卫,曹晔,马亚静

(陕西师范大学 数学与信息科学学院,陕西 西安 710062)

摘要:研究阶数0<α<1的分数阶不确定奇异系统的鲁棒镇定问题.利用矩阵奇异值分解和线性矩阵不等式方法提出新的基于观测器的鲁棒状态反馈镇定的充分条件, 同时给出该条件下观测器和状态反馈控制器的具体求解方法.最后通过数值例子验证该方法的有效性.

关键词:分数阶不确定奇异系统; 观测器; 反馈控制器; 线性矩阵不等式

0引言

利用分数阶模型能够更精确地描述一些复杂系统(如粘弹性材料电子电路和热传导等). 因此, 分数阶微积分作为一个有效的数学工具, 已被广泛应用于生物科学及工业工程等领域[1-2]. 稳定性问题是控制理论的一个重要分支,近年来分数阶系统稳定性研究受到学者们的关注[3-4].但是在实际系统中, 由于各种不可避免的因素,使得系统模型的建立常带有不确定性.文献[3]用Lyapunov方法研究了区间不确定分数阶系统的稳定性. 文献[4-5]分别给出了当0<α<1和1<α<2时区间不确定分数阶系统鲁棒稳定的充要条件.文献[6-8]用线性矩阵不等式的方法给出了设计分数阶系统的状态反馈或输出反馈控制器的充要条件.

奇异系统由微分方程描述的子系统和代数方程描述子系统构成, 分别表示状态变量的动态特征和静态关系. 与标准系统相比,奇异系统能更好地表示系统的物理特性, 且奇异系统的描述更为直接和适用. 因而奇异系统被广泛应用于电力系统[9], 经济系统等领域. 文献[10] 研究了分数阶奇异系统的稳定性, 文献[12-13]研究了0<α<2的分数阶不确定奇异系统的鲁棒渐进稳定性问题.以上方法均在状态已知的前提下使用，在实际中系统状态并不完全可知，因此需要基于观测器的控制.文中考虑基于观测器的不确定分数阶奇异系统的镇定问题.运用矩阵奇异值分解和线性矩阵不等式方法给出分数阶不确定奇异系统鲁棒渐进稳定的充分条件.采用以下记号: MT是M的转置,sym{X}=XT+X,⊗表示kronecker积.

1问题描述与预备知识

首先, 给出分数阶微分的Caputo定义:

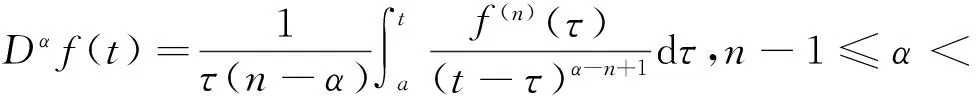
(1)

考虑如下分数阶奇异系统

(2)

其中α∈(0,1)为分数阶系统的阶数,E∈Rn×n为奇异矩阵,且rank(E)=r

定义1[6]对于分数阶奇异系统(2), 如果∃λ∈C, 使得|λαE-A|≠0,即|λαE-A|不恒为零, 那么(E,A)是正则的.

定义2对分数阶奇异系统(2), 如果系统是正则的, 脉冲自由且稳定的, 那么称系统是可容许的.

引理1[6,10]分数阶奇异系统(2)是可容许的, 如果下列条件同时成立:

(ⅰ) 若存在2个非奇异矩阵P和Q使得

PEQ=diag(Ir,N),PAQ=diag(A1,In-r),

(3)

其中A1∈Rr×r,N∈R(n-r)×(n-r)是幂零矩阵,系统(2)是正则的.

(ⅱ) 若deg(det(βE-A))=rank(E), 则系统(2)是脉冲自由的.

(ⅲ) 若系统(2)的有限特征值满足|arg(λ)|>πα/2,i=1,2,…,r,则系统(2)是稳定的.

考虑如下不确定分数阶奇异系统

(4)其中α∈(0,1)为分数阶系统的阶数,x(t)∈Rn是状态变量,u(t)∈Rm是控制输入,y(t)∈Rp是控制输出,A∈ Rn×n,C∈ Rp×n,E∈ Rn×n是系统矩阵, 且E为奇异矩阵, 并且rank(E)=r

系统(4)的观测器

(5)

(6)

其中

(7)

则系统(6)对应的自治系统为

(8)

其中

(9)

引理3[7]对任意矩阵Π∈ Rm × n且m

Π =U[S0]VT.

(10)

其中S=diag{σ1,σ2,…,σm}∈Rm× m,σ1≥σ2≥ ,…,≥σm>0,U∈ Rm× m,V∈ Rn×n是酉矩阵.

(11)

其中X11∈ Rm× m,X22∈R(n-m)× (n-m),V∈ Rn×n是酉矩阵.

引理5[13]对任意矩阵X,Y和合适维数的正定矩阵Q,有

XTY+YTX≤ XTQX+YTQ-1Y.

(12)

特别地, 当Q=εI时,有

XTY+YTX≤εXTX+(1/ε)YTY.

(13)

2主要结果

定理1对于正则系统(8),如果存在正定矩阵P1∈ Rn×n,P2∈ Rn×n,Q∈R2(n-r)×2n, 以及正数εi(i=1,2,3),使得矩阵

(14)

成立,则闭环系统(8)是鲁棒可容许的.其中

证明如果存在2个正定矩阵Q11和Q21, 2个反对称矩阵Q12和Q22以及Q∈R2(n-r)× 2n,使得

(15)

那么由引理2得系统(8)是可容许的.

令Q11=Q21=P0=diag(P1,P2),Q22=Q12=0,得

(16)

将

代入式(16)可得

(17)

应用引理5得

(18)

由F(t)FT(t)≤I得

(I2⊗F(t))⊗(I2⊗F(t))T=I2⊗(F(t)FT(t))≤I.

(19)

注意到θi1θi1T=I2(i=1,2),ΔA=MFN,由引理5,∀εi>0(i=1,2),有

(20)

类似以上讨论,可得

(21)

则

(22)

运用Schur补得不等式(22)等价于不等式(14).定理1证毕.

由于存在非线性项P1BK与P1L,P2L, 所以不等式(14)不是LMI. 通过奇异值分解方法,可将式(14)转换成LMI.

定理2对系统(4), 假设行满秩的矩阵B的奇异值分解为

(23)

其中，S1=diag(σ1,σ2,…,σm)∈Rm×m,σ1≥σ2≥…≥σm>0,U1∈Rm×m,V1∈Rn×n是酉矩阵.如果存在2个对称正定矩阵P1∈ Rn×n,P2∈ Rn×n和矩阵X1∈Rn×p,X2∈Rm×n,X3∈Rm× n,Q∈R2(n-r)×2n, 以及实常数εi(i=1,2,3),使得矩阵

(24)

成立.则闭环系统(8)是鲁棒可容许的.其中

其中P11∈ Rm× m,P22∈R(n-m)×(n-m),V∈ Rn×n是酉矩阵.

特别地, 在系统(8)的Acl的中去掉第二行第二列,容易得到如下推论.

推论1阶数0<α<1 的分数阶奇异不确定线性系统(4)在状态反馈输入u(t)=Kx(t)下是渐近稳定的,当且仅当存在一个矩阵X∈Rm×n, 一个对称正定矩阵P0∈Rn×n, 矩阵Q∈R(n-r)×n,3个标量εi>0(i=1,2,3),使得

其中

3数值算例

考虑形如式(4)的分数阶奇异不确定线性系统:α=0.8,

F(t)=diag(sin(0.1πt),cos(0.2πt),sin(0.1πt)).

A有2个稳定特征值-2.4142,-3.000和1个不稳定特征值0.414 2.不满足引理3中线性矩阵不等式(9),即当u(t)=0时, 系统(4)不稳定. 对矩阵BT作奇异值分解, 则

利用Matlab中LMI工具箱进行验证,不等式(14)是可行的, 这表明基于观测器的不确定系统(9)在状态反馈下是鲁棒渐进稳定的, 其中一个可行解为

K=[0.834 7-0.756 7-1.178 2], L=[1.270 9-0.177 2-0.401 6]T.

上述分数阶系统在状态反馈控制器下的时间响应曲线如图1所示.

4结束语

研究了阶数0<α<1的分数阶不确定奇异系统的鲁棒镇定问题. 用矩阵奇异值分解和线性矩阵不等式方法提出了新的基于观测器的鲁棒状态反馈镇定的充分条件, 同时给出了该条件下观测器和状态反馈控制器具体的求解方法.

参考文献(References):

[1]HILFERR.Applicationoffractionalcalculusinphysics[M].Singapore:WordSciencePublishing,2000.

[2]ORTIGUEIRAMD,MACHADOJAT.Specialissueonfractionalsignalprocessingandapplications[J].SignalProcessing,2003,83(11):2285-2480.

[3]TRIGEASSOUJC,MAAMRIN,SABATIERJ,etal.ALyapunovapproachtothestabilityoffractionaldifferentialequations[J].SignalProcessing,2011,91(3):437-445.

[4]AXTELLM,BISEEM.Fractionalcalculusapplicationsincontrolsystems[C]//ProceedingsoftheIEEE1990NationalAerospaceandElectronicsConference,Naecon,1990:563-566.

[5]SABATIERJ,MOZEM,FARGESC.Onstabilityoffractionalordersystems[C]//ProcessingoftheThirdIFACWorkshoponFunctionalDifferentiationanditsApplication,2008:1566-1576.

[6]YUYao,JIAOZhuang,SUNChangyin.Sufficientandnecessaryconditionofadmissibilityforfractionalordersingularsystem[J].ActaAutomSin,2013,39(12):2160-2164.

[7]LANYH,HUANGHX,ZHOUY.Observer-basedrobustcontrolofa(1≤α<2)fractional-orderuncertainsystems:Alinearmatrixinequalityapproach[J].ControlTheoryApplIET,2012,6(2):229-234.

[8]SABATIERJ,MOZEM,FARGESC.LMIstabilityconditionsforfractionalordersystems[J].ComputersandMathmaticsandApplications,2010,59(5):1594-1609.

[9]PARKJuH.DesignofrobustH∞filterforaclassofneutralsystems:LMIoptimizationapproach[J].MathematicsandComputersinSimulation,2005,70(2):99-109.

[10]DOYEIN,ZASASZINSKIM,DAROUACHM,etal.Stabilizationofsingularfractional-ordersystems:AnLMIapproach[C]//ProceedingsoftheIEEEMediterraneanConferenceonControlandAutomation,Marrakesh,2010:209-213.

[11]BOYDS,VANDENBERGHEL.Convexoptimization[M].Cambridge:CambridgeUniversityPress,2004.

[12]DOYEN,ZASADZOMSKIM,DAROUACHM,etal.Regularizationandrobuststabilizationofuncertainsingularfractional-ordersystem[C]//Preprintsofthe18thIFACWorldCongress,Milano,2011:15031-15036.

[13]DOYEIN,ZASADZINSKIM,DAROUACHM,etal.Observer-basedcontrolforfractional-ordercontinuous-timesystems[C]//Processingsofthe48thIEEEConferenceonDecisionandControl& 28thChineseControl,Shanghai,2009:1932-1938.

编辑、校对：师琅

文章编号:1006-8341(2016)02-0190-07

DOI：10.13338/j.issn.1006-8341.2016.02.010

收稿日期：2015-09-06

基金项目:国家自然科学基金资助项目(61403241，11771233)

通讯作者:吴保卫 (1963—),男,陕西省咸阳市人，陕西师范大学教授,研究方向为控制理论.

中图分类号：O 231

文献标识码：A

Stabilization of fractional-order singular uncertain systems

LILulu,WUBaowei,CAOYe,MAYajing

(College of Mathematics and Information Science, Shaanxi Normal University, Xi′an 710062, China)

Abstract:The stabilization for fractional-order singular(FOS) uncertain linear systems with the fractional commensurate order 0<α<1 was researched.By using the matrix singular value decomposition(SVD)and linear matrix inequality (LMI) technics, the sufficient conditions for robust state feedback stabilization based on the state observer were derived.The efficient approach were also presented for designing the observer and the state feedback controller under this condition. Finally, numerical example demonstrates the validity of this approach.

Key words:fractional-order singular uncertain systems; observer; feedback controller; linear matrix inequality (LMI)

E-mail:wubw@snnu.edu.cn

引文格式：李路路,吴保卫,曹晔,等.分数阶不确定奇异系统的镇定[J].纺织高校基础科学学报,2016,29(2)：190-196.

LI Lulu,WU Baowei,CAO Ye,et al.Stabilization of fractional-order singular uncertain systems[J].Basic Sciences Journal of Textile Universities,2016,29(2):190-196.