贝叶斯原理的不确定度评定方法比较
姜 瑞,陈晓怀
(合肥工业大学 仪器科学与光电工程学院,安徽 合肥 230009)
贝叶斯原理的不确定度评定方法比较
姜瑞,陈晓怀
(合肥工业大学 仪器科学与光电工程学院,安徽 合肥 230009)
针对仅依据测量样本信息进行不确定度评定的局限性,利用贝叶斯信息融合原理,分别研究了基于无信息先验、共轭先验和最大熵先验分布的测量不确定度评定与更新方法,使评定过程充分融合历史先验信息和当前样本信息,提高了测量不确定度评定的可靠性。仿真实例表明:无信息先验方法没有将各组测量数据融合,其仿真结果波动最大;共轭先验方法仿真结果波动较大,经过多次数据融合逐渐趋于理论值;最大熵先验方法仿真结果波动较小,经过数据融合逐渐趋近于理论值。
不确定度评定;贝叶斯原理;无信息先验;共轭先验;最大熵先验
0 引言
测量不确定度作为反映测量结果质量水平及可靠程度的重要指标,其评定方法越来越受到国内外学者的关注[1-5]。现有研究在评定测量不确定度时,有些仅依据历史经验、专家意见和先验资料[6],忽略了测量系统实测数据;有些仅依据测量样本信息,忽略了与测量系统历史信息的结合[7-9]。这些方法均不能充分反映测量系统的最新状态,影响了不确定度评定结果的可靠性和合理性。
基于贝叶斯信息融合的不确定度评定方法以贝叶斯统计推断原理为基础,能够充分融合历史先验信息和当前样本信息[10-12]。根据历史信息确定先验分布,通过贝叶斯模型融合先验分布和当前样本数据,继而推导出后验分布,实现对测量不确定度的评定及更新。
贝叶斯评定方法的关键在于根据历史信息合理确定先验分布,先验分布是贝叶斯统计模型的重要组成部分。现有文献对于贝叶斯先验分布有一定研究[13-15],但多数文献只是简单介绍某种先验分布方法,对于其优势、局限性以及适用范围并没有进行深入分析[13-14]。此外,很少有研究将贝叶斯及其先验分布方法应用于测量不确定度的评定及更新。因此,本文对基于无信息先验、共轭先验和最大熵先验的贝叶斯评定方法进行对比分析,对于合理测量不确定度评定具有重要的实际意义。
1 贝叶斯不确定度评定方法
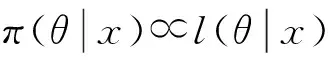
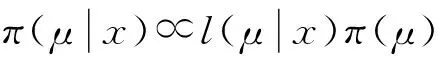

(1)
2 基于无信息先验的贝叶斯不确定度评定
2.1无信息先验分布

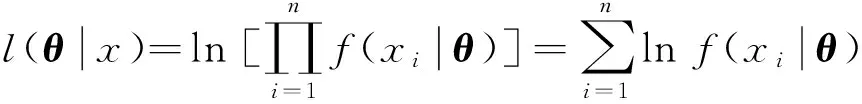
其Fisher信息阵为:
I(θ)=(Iij(θ))p×p;

则θ的无信息先验密度为:
π(θ)=[detI(θ)]1/2,
其中:detI(θ)表示p阶方阵I(θ)的行列式。
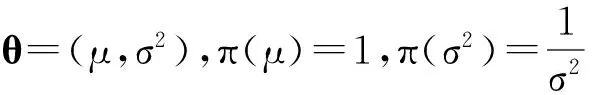

(2)
2.2无信息先验下的后验分布及不确定度
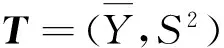
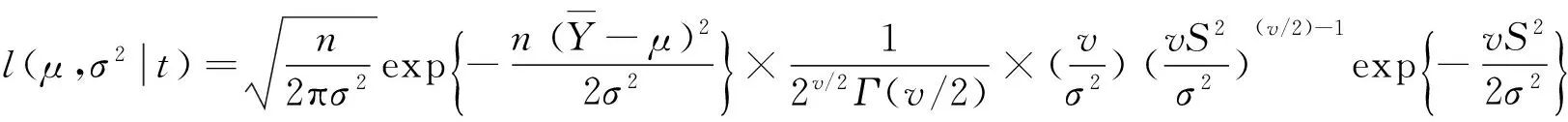
(3)
其中:μ为正态总体均值;σ为正态总体标准差;v为自由度。
结合式(2),由贝叶斯公式获得μ和σ2联合后验密度函数为:

(4)
即后验分布服从:
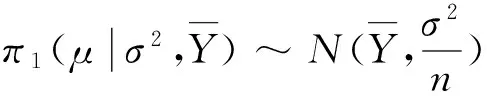
根据GUM和式(1)可知,基于无信息先验分布的后验分布最佳估计值及其标准不确定度为:

(5)
3 基于共轭先验的贝叶斯不确定度评定
在已知一定的先验信息和样本分布的情况下,可利用共轭贝叶斯方法进行不确定度评定。共轭贝叶斯方法的特点在于先验分布和后验分布形式相同,即后验分布融合了先验信息与样本信息之后只是相应地改变了其分布参数值,仍然与先验分布属于同一分布函数形式。另外,每一次信息融合后得到的后验分布可以作为后续评定的先验信息,如此反复应用,可以使测量信息得到持续更新。
3.1共轭先验分布
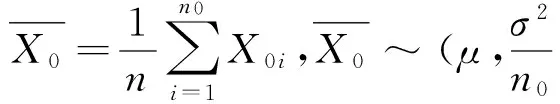
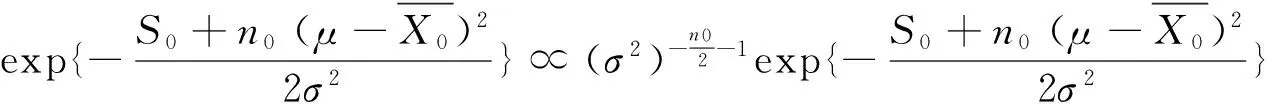
(6)
3.2共轭先验下的后验分布及不确定度
设样本的观测值为(X11,X12,…,X1n1),其似然函数为:
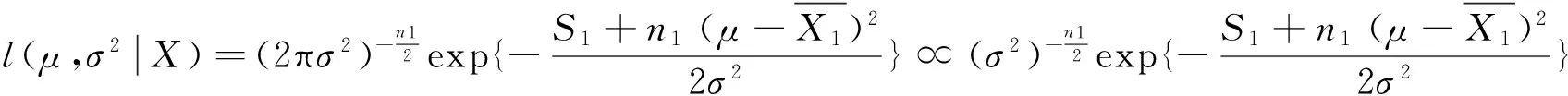
(7)
结合式(6),由贝叶斯公式获得μ和σ2联合后验密度函数为:

(8)

即后验分布服从:
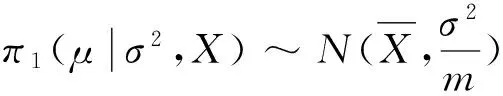
由GUM和式(1)可知,基于共轭先验分布下的后验分布最佳估计值及其标准不确定度为:
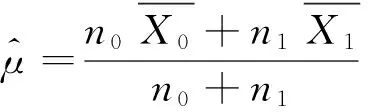
(9)
4 基于最大熵原理的贝叶斯不确定度评定
针对随机变量概率分布难以确定,且通常只能获得测量结果的均值和方差等特征值的局限性,采用最大熵原理确定先验分布和样本信息概率密度函数(probabilitydensityfunction,PDF),能够降低对随机变量概率分布的预测风险,使测量不确定度评定结果更加客观合理。
4.1最大熵原理确定先验分布和样本分布
假设一个随机变量x,其唯一的PDF即f(x)可以由最大熵函数H(x)获得:

f(x)约束条件为:

(10)
在熵函数中引入Lagrange乘子λi(i=1,2,…,n),得到:
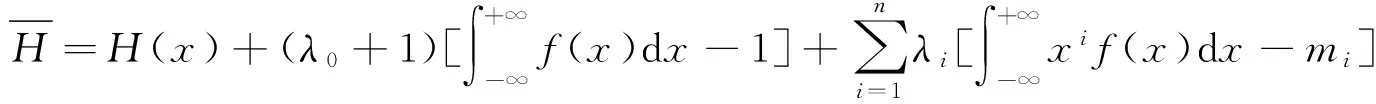
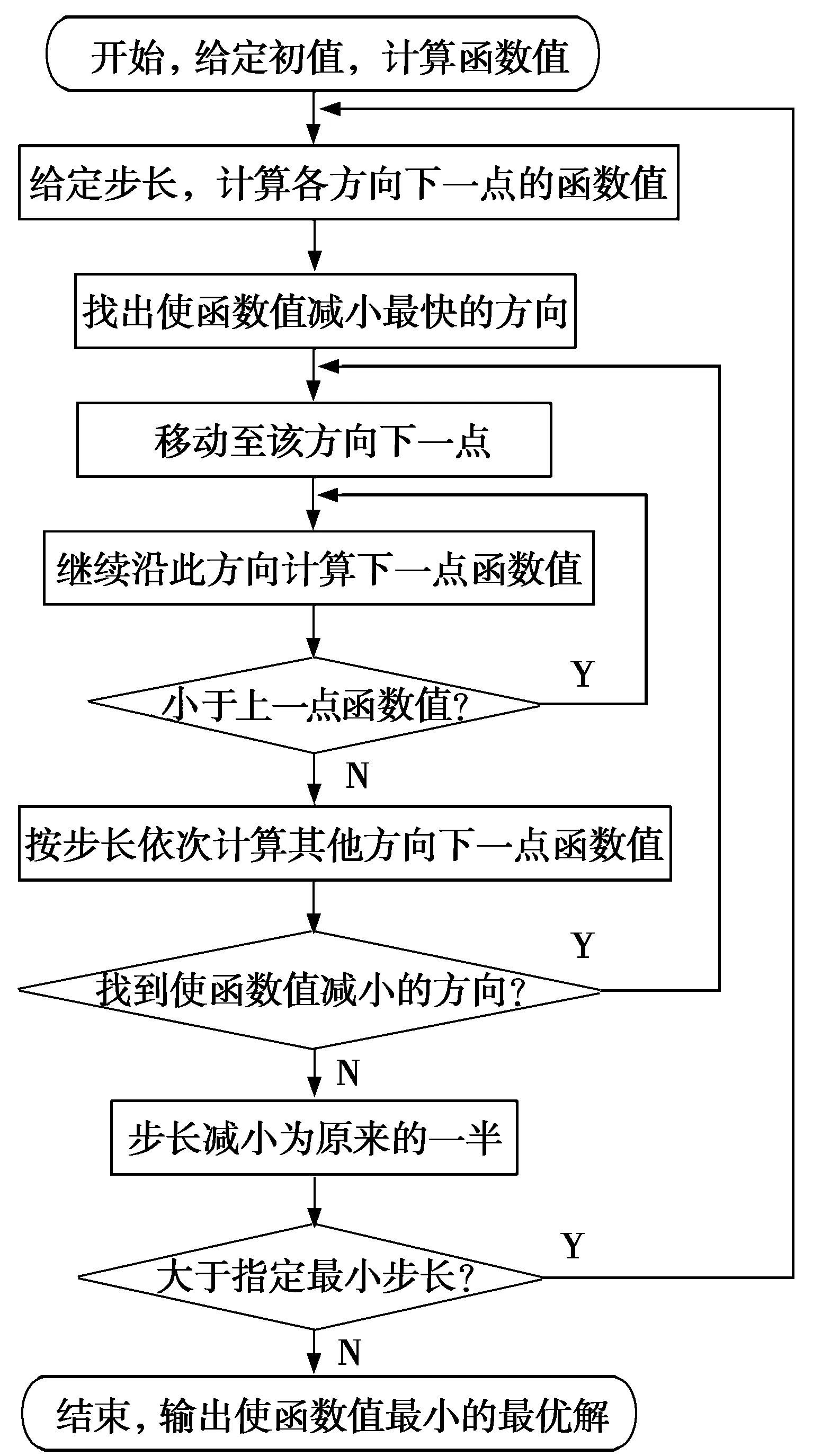
图1 爬山算法程序流程
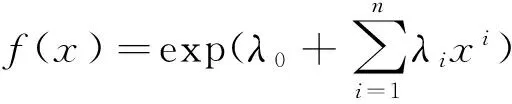
结合式(10),整理得:
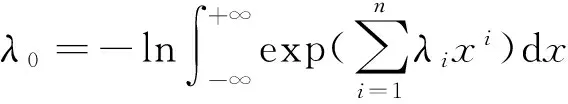
(11)
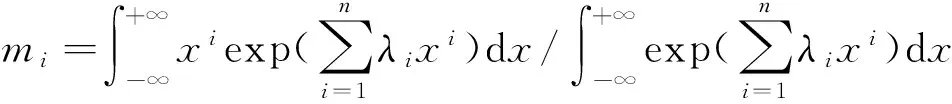
记残差ri为:
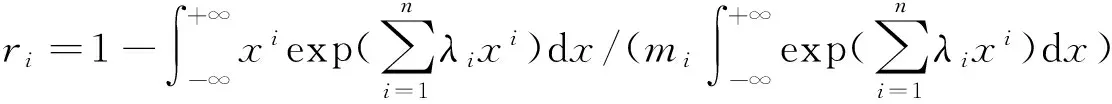

4.2最大熵先验下的后验分布及不确定度
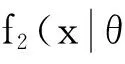
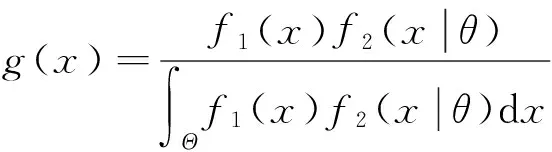
(12)
其中:Θ为参数空间。
由GUM可知,基于最大熵原理的后验分布最佳估计值及其标准不确定度表示为:

(13)
基于式(12)获得的后验分布,可作为后续评定的先验信息。结合式(13),可随着测量过程不断融入测量系统的最新信息,实现不确定度评定的连续更新。
5 MATLAB仿真
假设一个随机变量X服从正态分布N(30,0.022),利用MATLAB对X~N(30,0.022)随机抽样,按照抽样顺序得到8组随机数,见表1。
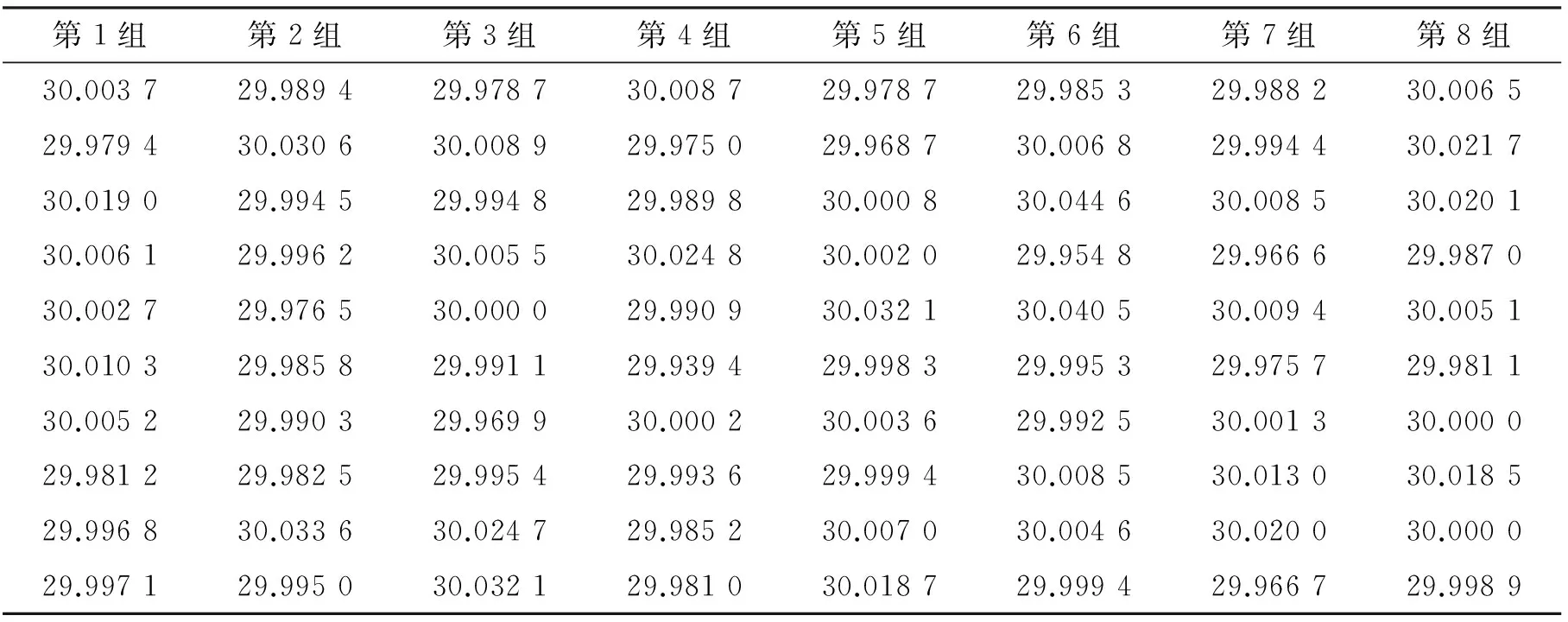
表1 MATLAB仿真随机抽样数据
5.1无信息先验贝叶斯不确定度评定
5.2共轭先验贝叶斯不确定度评定
以第1组数据为先验信息,计算其均值μ0、标准差σ0、方差S0及标准不确定度u0为:
μ0=30.000 15; σ0=0.012 3; S0=0.001 35; u0=0.012 3。
根据第2组数据得到S1=0.003 34,由式(9)求得融合先验数据和第1组数据的测量信息标准不确定度u1=0.016 7。
以第1次信息融合后的后验分布作为先验信息,根据第3组数据即新样本数据得到S2=0.003 25,由式(9)求得融合前3组数据的测量信息标准不确定度u2=0.019 7。重复上述计算过程,获得共轭先验贝叶斯不确定度评定与更新的仿真结果,见表2。
5.3最大熵先验贝叶斯不确定度评定
以第1组数据为先验信息,确定其积分区间为[29.979 4,30.019 0]。
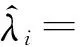
f1(x)=exp(221.962 8-19.315 4x+0.7x2-0.01x3)。
通过式(13)确定先验数据标准不确定度为:
u0=0.018 5。
将第2组数据作为样本信息,获得当前样本似然函数。首先确定其积分区间为[29.976 5,30.033 6],利用式(10)求得样本数据前3阶样本矩m′i=[30.028 4,900.950 3,27 015.105 4]。令
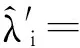
λ′0=-164.486,从而得出样本似然函数为:
f2(x)=exp(-164.486-21.430 7x+0.9x2),
代入式(12)求得后验分布PDF:g1(x)=exp(57.476 8-40.746 1x+1.6x2-0.01x3)。根据式(13)求得后验分布标准不确定度u1=0.022 6。
以融合前两组数据的后验分布g1(x)作为先验信息,同理获得第3组数据样本似然函数:f3(x)=exp(256.857 7-17.481 4x+0.9x2-0.02x3)。通过代入式(12)求得融合前3组数据的后验分布PDF:g2(x)=exp(315.614 5-56.227 5x+2.5x2-0.03x3)。根据式(13)求得后验分布标准不确定度u2=0.025 3。重复上述过程,获得最大熵先验贝叶斯不确定度评定与更新的仿真结果,见表2。

表2 3种贝叶斯不确定度评定方法仿真结果
5.4仿真结果分析
分析对比3种贝叶斯不确定度评定方法的仿真结果,如图2所示。
无信息先验贝叶斯不确定度只是通过贝叶斯统计推断获得每一组测量数据的不确定度,并没有将各组测量数据进行信息融合,该方法仿真结果波动大,适用于无任何先验信息或先验信息极少的情况。
共轭先验贝叶斯不确定度仿真结果波动较大,通过多次信息融合,能够逐渐趋于标准不确定度理论值。这种方法可利用历史数据和当前样本数据作为先验信息,即以后验分布作为进一步试验的先验信息,再进行评定试验,获得新的后验分布仍与先验分布属于同一个分布类型,可为后续不确定度评定提供合理前提。但共轭先验方法要求已知先验信息的具体分布类型,对于实际测量信息需要假定服从某种分布,产生一定主观风险。因此,共轭先验方法适用于已知测量信息分布类型的不确定度评定。

图2 3种贝叶斯不确定度评定方法仿真结果对比
最大熵先验贝叶斯不确定度评定仿真结果波动较小,通过信息融合能够趋近于标准不确定度理论值。这种方法不需要确定测量信息的具体分布类型,可有效避免因人为假定而引起的主观因素影响,提高先验分布和后验分布的可靠程度。引入最优化算法,利用计算机编程可以解决测量不确定度评定的最优化问题,使不确定度评定工作效率得到提高。实时融入最新测量数据,可实现评定结果的连续更新。最大熵先验不确定度评定方法对算法和编程能力有很高的要求,并且需要不断探索更加高效的最优化算法。
6 结束语
贝叶斯不确定度评定方法能够充分融合历史先验信息和当前样本信息,使测量信息的不确定度随测量过程实时连续更新,及时反映测量系统状态的最新信息。其中,无信息先验下的贝叶斯不确定度评定方法并没有融合实际测量数据,其不确定度评定和更新结果波动很大;而共轭先验和最大熵先验建立的贝叶斯不确定度动态评定模型,通过多次数据融合,不确定度趋于理论值,这两种方法下的不确定度评定和更新结果更加客观合理。
[1]中华人民共和国国家质量监督检验检疫总局.测量不确定度评定与表示:JJF1059.1—2012[S].北京:中国质检出版社,2012.
[2]李睿,曲兴华.工业机器人运动学参数标定误差不确定度研究[J].仪器仪表学报,2014,35(10):2192-2199.
[3]徐磊,陈晓怀.蒙特卡洛法评定坐标测量机直径测量不确定度[J].河南科技大学学报(自然科学版),2016,37(3):15-19.
[4]ELSTERC.BayesianuncertaintyanalysiscomparedwiththeapplicationoftheGUManditssupplements[J].Metrologia,2014,51(4):189-200.
[5]裴亚辉,张兵利.一种基于贝叶斯方法的多分类器组合优化算法[J].河南科技大学学报(自然科学版),2010,31(1):34-37.
[6]DESIMONIE,BRUNETTIB.Uncertaintyofmeasurementandconformityassessment:areview[J].Analyticalandbioanalyticalchemistry,2011,400(6):1729-1741.
[7]凌明祥,李会敏,黎启胜,等.含相关性的测量不确定度拟蒙特卡罗评定方法[J].仪器仪表学报,2014,35(6):1385-1393.
[8]李昕娣,罗怀洁.PTB220型压力传感器检定结果不确定度评估[J].气象科技,2014,42(6):983-985.
[9]BATTISTELLIL,CHIODOE,LAURIAD.Anewmethodologyforuncertaintyevaluationinriskassessment:Bayesianestimationofasafetyindexbaseduponextremevalues[C]//InternationalSymposiumonPowerElectronics,ElectricalDrives,Automation&Motion.IEEE,2008:439-444.
[10]IUCULANOG,NIELSENL,ZANOBINIA,etal.Theprincipleofmaximumentropyappliedintheevaluationofthemeasurementuncertainty[J] .IEEEtransactionsoninstrumentation&measurement,2007,56(3):717-722.
[11]ZHANGXM,ZHANGHZ.UncertaintyanalysisforpumptestbasedonmaximumentropyandMonteCarlomethod[C]//Proceedingsof2010IEEEthe17thInternationalConferenceonIndustrialEngineeringandEngineeringManagement.2010:1628-1631.
[12]FANGX,SONGM.Estimationofmaximum-entropydistributionbasedongeneticalgorithmsinevaluationofthemeasurementuncertainty[C]//IntelligentSystems(GCIS),2010SecondWRIGlobalCongressonIEEE.2010:292-297.
[13]杨颖涛,王跃钢,邓卫强,等.基于共轭先验分布的贝叶斯网络分类模型[J].控制与决策,2012,27(9):1393-1396.
[14]刘伯权,刘喜,吴涛.基于共轭先验分布的深受弯构件受剪承载力概率模型分析[J].工程力学,2015(4):169-177.
[15]SAIDAB,SHAHZADMK,ZAMAIE,etal.Experts’knowledgerenewalandmaintenanceactionseffectivenessinhigh-mixlow-volumeindustries,usingBayesianapproach[J].Cognitiontechnology&work,2016,18(1):193-213.
[16]刘彩丽,肖海林.基于布谷鸟搜索算法的认知车载网络频谱分配方法[J].桂林电子科技大学学报,2016,36(3):173-177.
[17]陈梦洁,万源,吴克风,等.混合鱼群优化算法的贝叶斯网络结构学习[J].河南科技大学学报(自然科学版),2016,37(4):41-45.
[18]IZBENKOY,KOVTUNV,KUZNETSOVA.ThedesignofBooleanfunctionsbymodifiedhillclimbingmethod[C]//InformationTechnology:NewGenerations,2009.ITNG'09.SixthInternationalConferenceonIEEE.2009:356-361.
国家自然科学基金项目(51275148);合肥工业大学青年教师创新基金项目(JZ2014HGQC0126)
姜瑞(1991-),女,山西霍州人,硕士生;陈晓怀(1954-),女,安徽怀宁人,教授,博士,博士生导师,主要研究方向为现代精度理论与应用.
2016-06-12
1672-6871(2016)06-0021-07
10.15926/j.cnki.issn1672-6871.2016.06.005
TB92
A

