基于相互作用积分法的压电裂纹边界元分析

雷 钧，刘和国，杨庆生

（北京工业大学机械工程与应用电子技术学院，北京 100124）

基于相互作用积分法的压电裂纹边界元分析

雷 钧，刘和国，杨庆生

（北京工业大学机械工程与应用电子技术学院，北京 100124）

为了获得更为精确高效的压电裂纹分析方法，推导了压电材料中基于相互作用积分计算裂尖场集中系数的计算公式，并成功应用于相应的边界元分析软件.应用此软件，对PZT-4压电材料在不同加载条件、不同的极化方向等情况下压电矩形板中的中心直裂纹以及边裂纹问题进行了分析，验证了相互作用积分法的路径无关性，并且计算出各型裂尖场集中系数，与相应的基于J积分法以及位移插值法获得的结果对比良好，说明该方法是一种高效准确的压电裂纹分析方法.

相互作用积分；边界元法；压电材料；强度因子；极化方向

压电材料因其独特的压电效应在智能材料与结构中得到了广泛的应用.但常见的压电陶瓷为脆性材料，断裂韧性低、缺陷敏感性高，在工作载荷下易发生断裂失效.因而对其进行断裂研究十分重要.

目前针对压电材料的断裂分析包括实验研究、理论分析以及数值模拟等.理论研究主要针对无限大压电体等特殊情况，如Suo等［1］和Pak［2］对无限大压电体绝缘裂纹平面问题给出了解析解.实验研究则主要针对静态断裂问题，如Park等［3-4］在1995年先后对PZT-4紧凑拉伸试件进行了断裂实验及三点弯实验.数值模拟方便快捷，具有重要的现实意义.Enderlin等［5］实现了压电J积分在有限元法中的运用.Rao等［6］和Yu等［7］实现了相互作用积分法在有限元法对压电材料断裂研究中的应用.Lei等［8-11］实现了 J积分法［12］、位移法、公式应力法在边界元法对压电材料断裂参数计算中的应用，数值验证了J积分法计算压电断裂参数的高精度.如Lei等［8］文中所述，由J积分计算各型场集中系数，有2种基本方法:一种是通过基于裂尖张开位移比率的插值公式获得；另一种是基于辅助场的解析公式提出的所谓相互作用积分法［13-14］获得.前者由于需要计算裂尖张开位移，这显然依赖于数值计算高应变梯度裂尖区域的应变分布精度，对于有限元等区域型数值方法而言，会严重依赖于局部网格划分.而后者相互作用积分法无需计算裂纹面参数，裂尖单元的选取对计算结果影响较小，在计算精度上更具优势.而与传统J积分法相比，相互作用积分法保留了J积分路径无关性的特点，同时与J积分法不同的是相互作用积分法可以直接得到各型应力强度因子，无需进一步分离，计算更为简单快捷.与传统位移法、公式应力法相比，相互作用积分法无需在裂纹面进行插值计算，计算结果具有更高的精度.J积分公式在有限元实现时，需引入一个光滑的权函数将围道积分转化为等效的区域积分，其迭代插值得到的计算结果对单元划分具有高敏感度.而边界元法可直接进行J积分中的围道积分，无需插值迭代，相对简单高效.而据作者所知，目前，还未见在边界元法中采用相互作用积分法计算压电断裂参数的相关文献.因此，本文将压电材料中基于相互作用积分公式，应用于相应的边界元分析软件，实现对压电材料中的裂尖断裂参数的计算，并与J积分、位移法等计算结果进行对比.

1　压电方程

令σ、u、D分别表示应力张量、弹性张量和电位移张量.在准静电场假设以及无体积力和体电荷情况下，二维线性均匀、各向异性压电体的平衡方程如下:

式中Δ表示哈密顿算子.

令ε、E分别表示应变张量和电场张量，它们分别为位移u和电势φ的梯度

压电体的本构方程可表示为

式中:C、e、κ分别为4阶弹性张量、3阶压电张量和2阶介电张量，三者满足对称性

2　边界积分方程

对于二维压电裂纹体，其外部边界记为∂Ω，裂纹面ΓC由上裂纹面Γ+C与下裂纹面Γ-C组成，即ΓC=Γ-C+Γ+C.引入广义位移张量u=［ui，φ］T，应力σ=［σij，Di］T，应变 ε=［εij，-Ei］T，面力 p= σiJn，并定义广义张开位移为ΔuJ=uJ（x∈Γ+C）-uJ（x∈Γ-C）.

假设压电裂纹满足Deeg［15］提出的绝缘型裂纹面电边界条件，借助Lei等［8］文中的对偶边界积分方程法，分别对外边界∂Ω与裂纹面Γ+C应用位移及面力边界积分方程式中:x和y分别表示源点和观察点；cIJ=δIJ/2是边界平滑参数；uGIJ和pGIJ分别为二维压电体静态位移与面力基本解；dGIJ和 sGIJ表示其高阶基本解，具体表达式可参考文献［16］.

3　相互作用积分

裂纹尖端的局部应变能释放率可由与积分路径无关的J积分公式计算获得，二维均匀压电介质的J积分表达式由Pak［12］给出:

式中:Γ为围绕裂尖的任意闭合积分路径；nj表示闭合积分路径的单位外法向量分量，W=σiJεiJ/2为线性压电的电焓密度.

考虑压电断裂模型2个独立的平衡状态:一个是基于实际加载条件下的真实场状态；另外一个是适用于任一断裂模型裂尖场的辅助场状态.定义在真实载荷与辅助场联合作用下的J积分记为JTol，表达式为

其中上标“aux”表示辅助场的力学与电学变量，

I表示相互作用积分，应用等式

相互作用积分I可表示为

Rao和Kuan［6］定义二维Griffith裂纹尖端场作为辅助场变量，具体表达式为

式中:裂尖场的强度因子K=［K∀，KⅠ，KD］T；fNiJ（θ）和dNI（θ）表示均匀压电体的标准角函数，具体表达式见文献［6］.

在数值计算时，可取围道积分路径，如图1所示.

进一步将围道离散成N个二次连续单元，每个单元取的高斯点的个数为k，则式（11）离散为

式中:L为雅克比矩阵；wm表示高斯点的权重.

与J积分类似，压电材料的相互作用积分可表示为

式中:Y为与材料参数的有关的Irwin矩阵，特殊地，如果取∀型裂纹的辅助场，即Kaux

∀=1，Kaux

Ⅰ=KauxD= 0，式（15）满足

同理，对于其他类型裂纹，可得

综上所述，广义应力强度因子可由求解下列方程得到:

4　数值算例

以下的算例中以常见的PZT-4压电材料作为研究对象，其材料参数为

裂尖场强度因子的量纲一计算公式为

4.1矩形压电板中心直裂纹强度因子计算

第1个算例取如图2所示含中心直裂纹的PZT-4矩形压电板，具体尺寸为:2W=1.0 m，2L= 2.0 m，2a=0.2 m，在x2方向施加载荷（σ022，D02），令加载参数为λ=c22D02/（e22σ022），取图3所示3个围道积分路径（以右裂尖为中心，边长分别为0.18、0.2、0.22 m的正方形围道路径1、路径2、路径3，在表1中记为P1、P2、P3），分别通过相互作用积分计算不同加载条件下的强度因子，并将结果与J积分及位移法结果进行对比，如表1所示.相互作用积分结果与J积分结果最大误差小于0.25%，充分证明了相互作用积分的高效准确性与路径无关性.

对上述含中心裂纹的PZT-4压电板，取路径2为计算路径，分别对每个二次单元取不同的高斯点数，力电强度因子变化情况如图4所示.由图4可以看出，在不同加载条件下，高斯点的选取对压电板不同加载条件下力电断裂参数的计算结果基本没有影响.

4.2矩形压电板边裂纹强度因子计算

图5所示含边裂纹的矩形压电板，极化方向为沿着x2轴方向，具体尺寸为:2W=5 cm，2L=4 cm，2a=1.2 cm，由于算例4.2中已经论证了相互作用积分的路径无关性，为减少计算量，取图5所示2条围道作为积分路径（以右裂尖为中心，边长分别为1.2 cm和1.6 cm的正方形围道P1、P2），每个单元取20个高斯点，分别计算在不同加载条件下含边裂纹PZT-4压电板的断裂参数，并将相关结果与位移法、J积分法结果进行对比，相互作用积分结果与J积分结果最大误差小于0.6%，充分证明了相互作用积分的高效准确性与路径无关性，如表2所示.

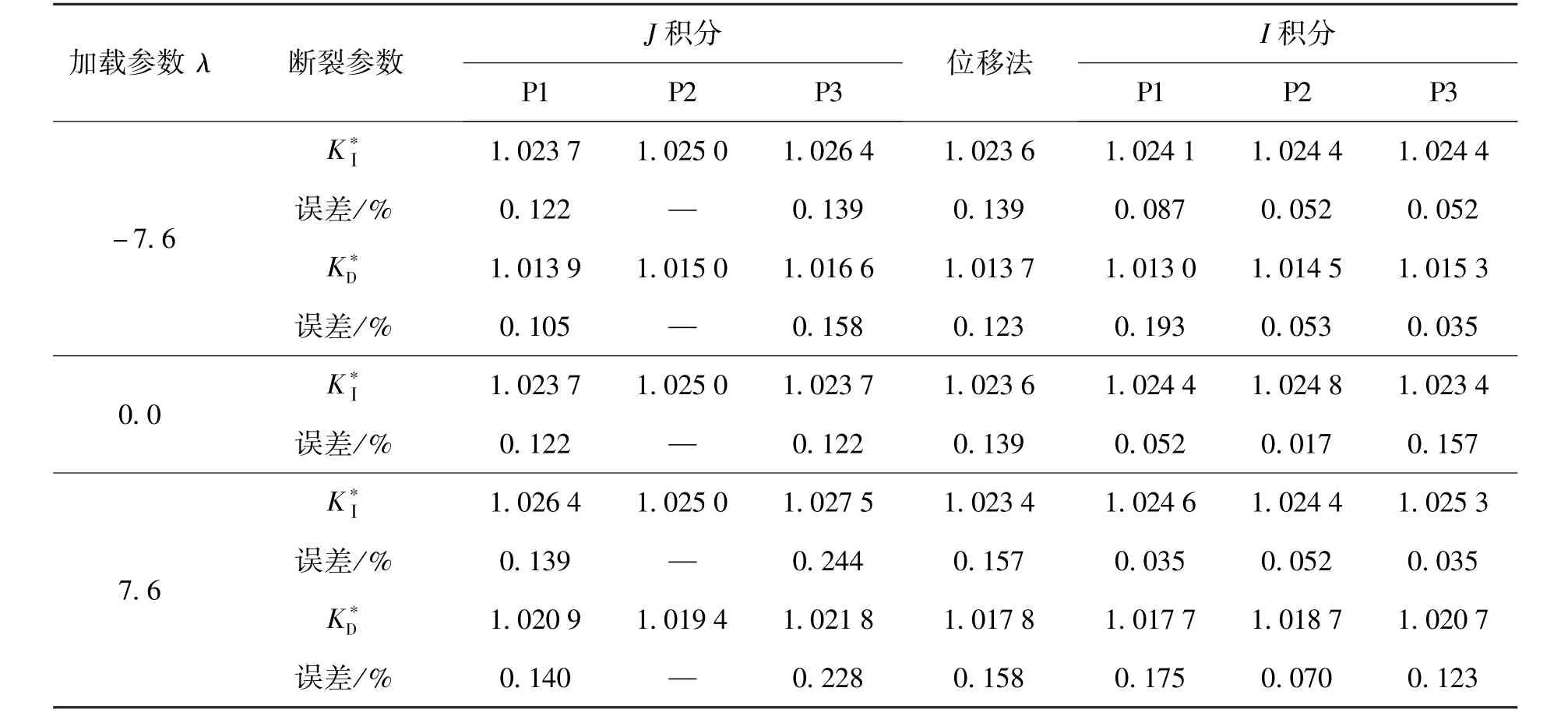
表1　中心直裂纹λ=-7.6,0,7.6加载断裂参数Table 1 Fracture parameter for the center crack under λ=-7.6,0,7.6 loading

表2　边裂纹λ=-7.6、0、7.6加载断裂参数Table 2 Fracture parameter for the edge crack under λ=-7.6,0,7.6 loading

4.3极化角度对断裂韧性的影响

对上述含中心裂纹的PZT-4压电板，取极化方向垂直于裂纹面方向为0°，于极化方向为90°，分别计算极化角度为0°～90°PZT-4压电板在力电耦合（σ022=1 GPa，D02=1 C/m2）作用下的断裂参数力电强度因子变化情况如表3所示.为减少计算量，相互作用积分结果只与位移法结果进行了对比.

由表3中数据可知，2种方法对比良好，最大误差不超过0.2%.2种计算方法均表明在相同加载条件下:PZT-4压电板在极化0°时电位移强度因子最大，而应力位移强度因子随着极化角度变化基本保持不变.

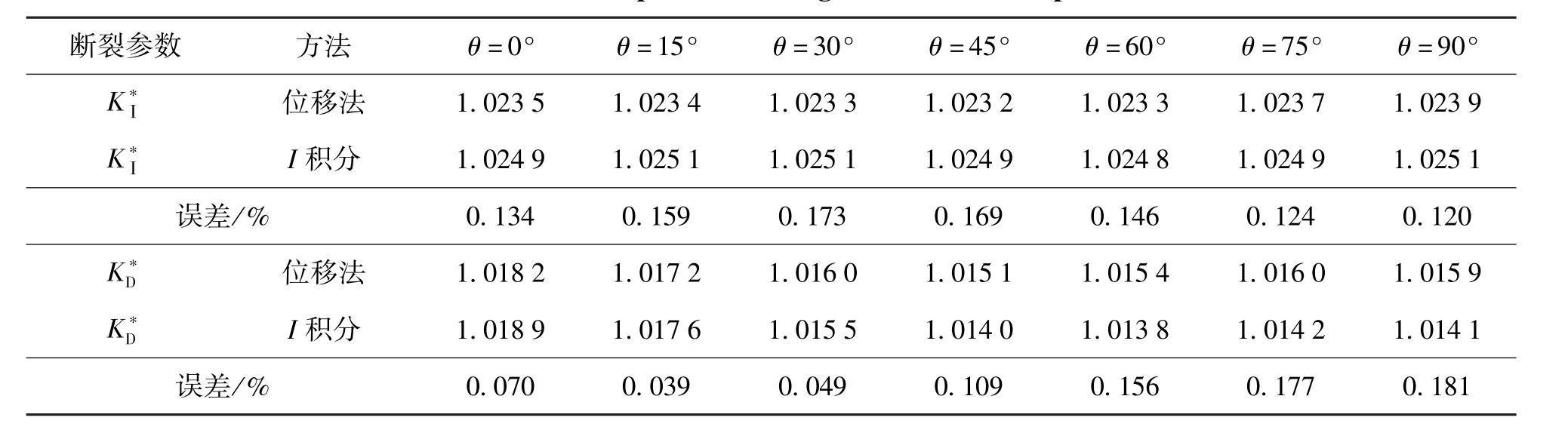
表3　极化角度对PZT-4压电板断裂参数的影响Table 3 Influence of polarization angle on the fracture parameter

5　结论

1）在计算压电材料断裂参数时，本文提出的基于边界元法的相互作用积分是精确高效的.

2）采用相互作用积分计算含中心裂纹及边裂纹PZT-4压电板在不同加载情况下的断裂参数时与J积分、位移法对比良好，且计算结果与围道积分路径无关.

3）相互作用积分采取了围道积分进行计算，围道积分上每个单元选取的高斯点的个数对不同加载情况下压电板断裂参数计算结果影响不大.

4）相互作用积分法与位移法均表明PZT-4压电板在极化0°时电位移强度因子最大，而应力位移强度因子随着极化角度变化基本保持不变.

［1］SUO Z G，KUO C M，BAMETT D M，et al.Fracture mechanics for piezoelectric ceramics［J］.Journal of the Mechanics and Physics of Solids，1992，40（4）:739-765.

［2］PAK Y E.Linear electroelatic fracture-mechanics of piezoelectricmaterials［J］.InternationalJournalofFracture，1992，54（1）:79-100.

［3］PARK S B，SUN C T.Fracture criteria for piezoelectric ceramics［J］.Journal of the American Ceramic Society，1995，78（6）:1475-1480.

［4］PARK S B，SUN C T.Effect of electric-field on fracture of piezoelectricceramics［J］.InternationalJournalof Fracture，1995，70（3）:203-216.

［5］ENDERLIN M，RICOEUR A，KUNA M.Finite element techniques for dynamic crack analysis in piezoelectrics ［J］.International Journal of Fracture，2005，134（3）: 191-208.

［6］RAO B N，KUNA M.Interaction integrals for fracture analysis of functionally graded piezoelectric materials［J］. International Journal of Solids and Structures，2008，45 （20）:5237-5257.

［7］YU H J，WU L Z，GUO L C，et al.A domainindependent interaction integral for fracture analysis of nonhomogeneous piezoelectric materials［J］.International Journal of Solids and Structures，2012，49（23）:3301-3315.

［8］LEI J，WANG H Y，ZHANG C Z，et al.Comparison of several BEM-based approaches in evaluating crack-tip field intensity factors in piezoelectric material［J］.International Journal of Fracture，2014，189（1）:111-120.

［9］LEI J，ZHANG C Z，FELIPE G S.BEM analysis of electrically limited permeable cracks considering Coulomb tractions inpiezoelectricmaterials［J］.Engineering Analysis with Boundary Elements，2015，54:28-38.`

［10］LEI J，WANG H Y，ZHANG C Z，et al.Crack-tip amplificationandshieldingbymicro-cracksin piezoelectric solids-Part I:Static case［J］.Engineering Analysis with Boundary Elements，2013，37（12）:1585-1593.

［11］LEI J，YANG Q S，ZHANG C Z.Transient response of a semi-permeablecrackbetweendissimilaranisotropic piezoelectriclayersbytime-domainBEM［J］. Engineering Analysis with Boundary Elements，2013，37 （10）:1205-1211.

［12］PAK Y E.Crack extension force in a piezoelectric material［J］.Journal of Applied Mechanics，1990，57 （3）:647-653.

［13］RAO B N，RAHMAN S.Mesh-free analysis of cracks in isotropic functionally graded materials［J］.Engineering Fracture Mechanics，2003，70（1）:1-27.

［14］RAO B N，RAHMAN S.An interaction integral method for analysis of cracks in orthotropic functionally graded materials［J］.Computational Mechanics 2003，32（1）: 40-51.

［15］DEEG W F J.The analysis of dislocation，crack，and inclusion problem in piezoelectric solids［D］.Stanford: Stanford University，1980.

［16］FELIPE G S，ZHANG C Z，ANDRES S.2-D transient dynamic analysis of cracked piezoelectric solids by a time-domain BEM［J］.Computer Methods in Applied Mechanics and Engineering，2008，197（33）:3108-3121.

（责任编辑 杨开英）

Analysis of Boundary Element for Piezoelectric Cracks Using an Interaction Integral Method

LEI Jun，LIU Heguo，YANG Qingsheng
（College of Mechanical Engineering and Applied Electronics Technology，Beijing University of Technology，Beijing 100124，China）

To get a more effective and accurate method to study the fracture behavior of the piezoelectric materials，a computational formula based on the interaction integral method to calculate the crack-tip field intensity factors was obtained in this paper.This method was successfully applied to the boundary element analysis software.With this software，the fracture behavior of PZT-4 made piezoelectric board's central crack and edge crack under different loading conditions was analyzed in different polarization directions. The path-independent characteristics of the interaction integral method was verified.The crack-tip field intensity factors obtained were compared well with the results of both the J integral method and the displacement interpolating method.This proves that this method is effective and accurate.

interaction integral；boundary element method；piezoelectric material；intensify factors；polarization direction

U 461；TP308

A

0254-0037（2016）02-0161-06

10.11936/bjutxb2015030009

2015-03-04

国家自然科学基金资助项目（11472021）

雷 钧（1976—），男，副教授，主要从事新型智能材料力学性能评价、数值计算技术方面的研究.E-mail:leijun@ bjut.edu.cn