基于提升小波的机械振动信号自适应压缩感知
王怀光,张培林,吴定海,范红波
(军械工程学院 车辆与电气工程系,河北 石家庄,050003)
基于提升小波的机械振动信号自适应压缩感知
王怀光,张培林,吴定海,范红波
(军械工程学院 车辆与电气工程系,河北 石家庄,050003)
针对复杂装备状态监测所面临的海量数据采样与传输问题,提出一种基于提升小波的自适应压缩感知方法。针对方法中提升小波信号处理中最优参数确定问题,利用稀疏度作为控制因子对提升小波滤波器和分解层数进行优选,并结合分块阈值降噪方法实现对机械振动信号的最佳稀疏分解。基于分块压缩感知的思想和满足RIP条件下观测次数下限的指导原则,解决提升小波分解各节点信号观测数据量的确定问题,构建基于提升小波的自适应压缩感知的机械状态监测体系。研究结果表明:该方法能够有效地减少压缩感知观测数据量,提高信号的重构速度和重构质量。
自适应压缩感知;稀疏度;提升小波;数据压缩;机械振动;状态监测
为了实时掌握装备运行状态信息,应用了基于CAN(controller area network)总线的分布式状态监测网络,其前端分布式节点通过传感器采集各关键部件的响应信息,所测数据不仅包含慢变信号,如油温、水温、油压、转速等,还包含机械振动等快变信号,机械振动信号多为动态复杂非平稳信号,传统的以Shannon或Nyquist采样定理为基础的信息获取对信号的采样频率要求越来越高,常常会造成海量数据,给数据通信带来一定的困难。压缩感知(compressed sensing)是近年来提出的一种集采样与压缩为一体的新的信息获取与信息处理理论[1−2],以远低于信号Nyquist频率的采样率对信号进行采样,可大大减少状态监测时所采集数据量。然而压缩感知与信号的最高频率无关,而与信号的稀疏性密切相关,而工程实测信号并非都是稀疏的,因此,首先需要将信号转换到具有稀疏特性的某已知变换域,利用信号在该域上的稀疏逼近来表示。信号的稀疏性是进行压缩感知准确重建的前提条件。文献[3−6]应用离散余弦变换、小波稀疏分解特性,对图像、语音等信号进行压缩感知,特别是文献[7]结合传统小波的多尺度分解,对高频系数进行压缩感知,以稀疏度的4倍来确定观测次数,并不具有广泛的适用性,常常导致数据的溢出,不适合机械振动监测领域等复杂信号的应用。本文作者针对机械状态监测信号的特点,利用提升小波变换提出了一种集信号降噪和数据压缩为一体的机械振动信号自适应多尺度压缩感知方法,分析了滤波器和分解层数对提升小波分解的稀疏度的影响,并结合分块阈值方法对分解系数进行降噪,提高了信号的稀疏度,借鉴分块压缩感知的思想并基于稀疏系数观测次数下界的指导原则,确定各层分解系数的压缩感知观测次数,能够在有效减少观测数据量,实现对振动信号数据压缩效果的同时预制噪声干扰,保留有用信息,提高压缩感知重构速度和重构质量,通过仿真信号和实测信号的对比分析验证了其有效性和良好的应用前景。
1 基于提升小波变换的信号稀疏表示
1.1提升小波变换
提升小波变换能够实现信号的稀疏分解,从而有利于信号的压缩等后续处理,数据长度为2M的提升小波分解过程为[8]:
1) 分裂。尺度j下低频系数cj[k]分裂为奇样本和偶样本。



提升小波继承了经典小波多分辨率特性,运算速度快,占用空间小,并且变换后数据长度不变。
1.2稀疏度控制因子
信号的稀疏程度直接关系到后续信号处理的质量,所分析的信号并非都是稀疏信号,这就需要先对信号进行稀疏分解。信号的稀疏表示具有很多的优良特性,能有效进行数据压缩和特征提取。
信号分解一般是基于完备正交基分解,设n维Hilbert空间中存在一组完备正交基{ϕi},则对任意一个n维信号s,下信号分解形式为

提升小波变换采用尺度滤波器和细节滤波器组成完备的小波基,提升小波对信号的分解,将信号在小波基上展开,其实是运用滤波器组去匹配原信号,若所选择的滤波器形貌与所要分析的信号最相似,则匹配效果好,分解变换后的小波系数的稀疏性更好,小波分解后,大的细节系数几乎都是成块出现的,体现了“稀疏簇聚”特征。由于小波滤波器有Haar,Daubechies,Symlet和Coiflets系列等,它们形态各异,不同滤波器的选择对信号分解的稀疏程度密切相关,分解层数越多,分解越细,分解层数也是需要考虑的另一个重要参数。
为合理确定滤波器和分解层数,定义了稀疏度来对信号分解的稀疏程度进行定量描述。
定义1 对于一个离散的真实信号x∈RN×1,信号的稀疏度K为

结合小波阈值处理的信噪分离原理,达到有效计算分解后提升小波系数的稀疏度,假设确定的阈值为T,则可计算分析信号S0的稀疏度:

提升小波分解信号的稀疏度等于各节点小波系数稀疏度之和。为实现对信号的最佳稀疏分解,便于后续的压缩感知,以稀疏度控制因子作为控制指标,优选提升小波变换的滤波器和分解层数,从而提高信号稀疏分解的效果。
1.3提升小波系数分块阈值降噪处理方法
状态监测信号难免含有噪声,为进一步提高信号稀疏度,抑制噪声干扰,将信号降噪融合于数据压缩过程,提高压缩感知的效果。分块阈值在阈值估计时考虑邻域小波系数的影响,提高了估计精度和收敛速度,具有较好自适应性、渐近最优性和均方误差特性,分块阈值具体算法如下[9]:
1) 对提升小波分解节点系数ωi进行分块bi,取块长度为L0=[(logn)/2],边界处的块长度取实际长度。
2) 对块长度进行扩展L=L0+2L1(其中L1=max(1,[L0/2]),为扩展块Bi)。
3) 利用扩展分块来估计块bi的收缩阈值


4) 对所有系数块bi,采用软阈值方法处理。

其中:kib∈ω。
2 提升小波自适应多尺度压缩感知
2.1压缩感知原理
在监测系统中,传统的数据压缩模式是先采样,编码压缩后进行数据传输,接收数据后进行解压缩,而压缩感知的核心思想是将压缩和采样合并进行,先对采集信号的非自适应线性投影(测量值),再根据相应重构算法由测量值重构原始信号。压缩传感理论主要包括信号的稀疏表示、观测采样和重构算法等3个方面[10−12]。
1) 稀疏信号。待测信号并非都是稀疏的,对于非稀疏信号需要进行稀疏变换,给定一组基,对于信号x可以表示为Ψ的线性组合形式:

2) 观测采样。对于在适当选择的基Ψ上具有稀疏描述的信号x∈RN,构建一个观测矩阵(M << N),获得信号x在观测矩阵Φ上的投影:

式中:y为测量向量;Φ为测量基,ΦΨ称为传感系统,从而实现对原信号的压缩采样,常用的观测矩阵有随机矩阵和确定性观测矩阵两大类。
3) 信号重构。信号的重建本身是一个欠采样条件(M << N)病态的求逆问题,结合信号稀疏性的优势,通过寻找满足y中的M个测量向量的最稀疏信号,即信号x是下列l0最小化问题的解:

为了方便求解,一般将上述NP-hard问题转化为最小化l1问题进行求解,目前信号重构已有很多算法,主要包括凸优化方法、贪婪算法和组合算法3类。
2.2自适应多尺度压缩感知
提升小波对信号进行分解后,各层节点的信号的稀疏度是不同的,采用同样的观测次数显然不合适,为了保证信号能够精确重构,必然要采用较高的观测次数,这对于稀疏度较大的节点信号来说,造成计算资源的浪费。因此,本文提出一种提升小波自适应多尺度压缩感知,如图1所示。

图1 提升小波自适应多尺度压缩感知Fig. 1 Adaptive multiscale compressed sensing of lifting wavelet transform
图1所示为基于提升小波自适应多尺度压缩感知的分布式机械状态监测数据采集传输过程。首先,前端的智能节点对信号进行多层提升小波分解,计算各层节点信号的稀疏度,并反馈控制提升小波滤波器和分解层数的优化选择,同时,节点信号的稀疏度也正好指导下一步压缩感知的观测次数的确定,从而在保证信号重构精度的条件下,实现对测试信号的最大限度压缩,减少后续CAN总线所需传输的数据量。CAN总线将观测数据传输到上位机后,利用上位机强大计算能力,重构出各节点的细节或近似信号,再利用提升小波重构得到原测试信号,进而进行相关的信号处理,实现对机械运行状态的实时监测和故障诊断。
对于稀疏度为k的节点信号,需要知道观测次数的下限,才能够合理确定观测次数。
2.3观测次数下限
对于k稀疏信号x可以实现精确重构的充分条件是观测矩阵Φ对于任意和常数δk∈(0,1)有k阶约束等距性,即
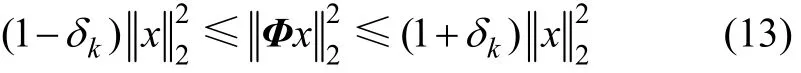
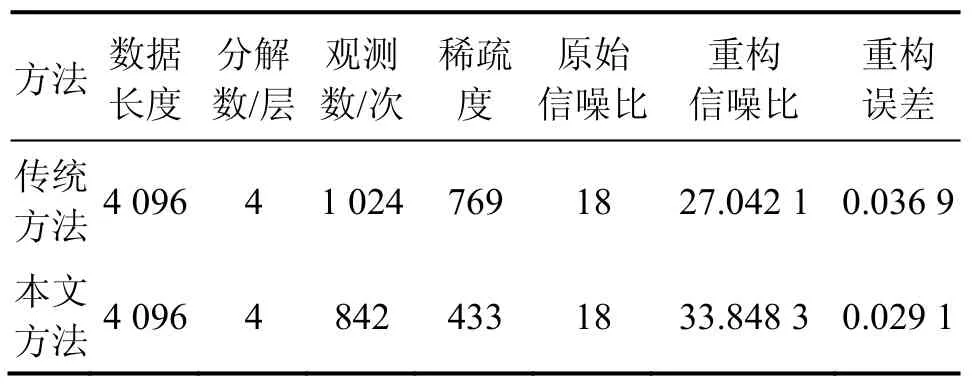
对于观测矩阵Am×n满足以上RIP准则时,如果k 结合观测矩阵的RIP准则和上述特性,可以得出: 进而推导出满足精确重构条件下的观测数下限为[13] 其中,0.28C≈。 因此,对于本文所提的基于提升小波自适应多尺度的机械振动信号压缩感知各节点观测次数取值如下: 在合理选取阈值,确定稀疏度的条件下,为保证重构质量,其中:C1取1.1C~1.5C,C2可取1.0~1.2。 3.1仿真信号分析 下面运用仿真信号来验证上述方法的有效性。产生含噪信号Blocks信号,长度为4 096,信噪比为18,如图2所示。 图2 含噪仿真信号Fig. 2 Simulated signal containing noise 为确定提升小波变换各参数,对含噪信号进行提升小波分解,以稀疏度因子为控制指标,试验中所选用的滤波器为Matlab库函数中常用的提升cdf4.6,haar,db7,sym6,bs3和9/7小波,分解层数设置为1~8层分解,对分解信号各节点进行的分块阈值降噪,计算其稀疏度,如图3所示。 图3 滤波器与分解层数对分解信号稀疏度的影响Fig. 3 Signal sparsity influence factors of filters and decomposition layers 从图3可见:不同的滤波器对分析信号的表现差异较大,有的滤波器随小波分解数的增加,稀疏度几乎不变,另外,也并非分解数越多就越稀疏,为了达到定量描述,表1所示为不同滤波器和分解数下的信号稀疏度。可见:对于Blocks信号,haar滤波器能够实现对分析信号的最佳匹配,实现最佳稀疏分解,从分解层数和计算量综合考虑,4层分解便可实现稀疏度高、效果好的稀疏分解。 表1 不同滤波器和分解数的信号稀疏度Table 1 Signal sparsity of different filters and decomposition layers 图4 重构信号效果比较Fig. 4 Comparison of signal reconstruction of different methods 从图4可以看出:传统的压缩感知方法重构的信号还存在许多毛刺,平滑性差,而本文压缩感知方法的重构信号更好地保留了原信号的特征,有效地抑制了噪声的影响。 表2所示为传统压缩感知方法与本文方法对仿真信号的分析结果。由表2可见:同样采用haar滤波器进行4层分解,本文采用的自适应多尺度压缩感知,提高了分解后信号的稀疏度,结合观测数下限的估计,自适应确定观测数,在较小的观测数下,能够更好地重构出原信号。 表2 仿真信号压缩感知效果比较Table 2 Compressed sensing results of simulated signal 3.2实测信号分析 实测齿轮振动信号来自于一个二级传动齿轮箱,包含2对齿轮副,齿数分别为25/50和18/91,输入轴转速为1 491 r/min,采样频率为6.4 kHz。实验中采集了齿轮5种状态下的振动加速度信号,即正常状态、中间轴齿轮齿根裂纹、中间轴齿轮齿面磨损、输出轴齿轮齿根裂纹和输出轴齿轮齿面磨损。本文以中间轴齿轮齿面磨损为例,振动信号取自相应齿轮轴的轴承座上方。计算可以得到齿轮啮合频率为621 Hz,中间轴齿轮故障频率为12.5 Hz。如图5(a)所示为故障信号的时域波形。可见:实测信号虽然能够看出机械冲击特征,但是被背景噪声干扰较为严重。 根据本文的方法,经过优选的滤波器为提升db5小波,能够很好地匹配机械振动信号冲击衰减特性,并确定最佳分解数为5层,获得各节点数据为[128,128,256,512,1 024,2 048],经提升小波分解后总稀疏度为3 126,由本文方法得到各小波树节点观测数为[82,80,169,352,706,797],即观测数据点数仅为2 186,由标准的匹配追踪重构算法重构得到原信号如图5(b)所示。从图5可知:压缩感知重构信号在大幅度压缩信号长度的情况下仍有效地保留了原信号的冲击形貌特征,抑制了噪声的干扰。 图5 齿轮箱实测信号及压缩感知重构信号Fig. 5 Reconstruction of gear box vibration signal 为进一步验证该压缩感知方法重构信号的质量,对重构信号进行进一步分析,在机械状态监测领域,主要是分析齿轮箱的频谱,查看相应的故障频率,因此,在本文中由于故障频率主要在于低频,故取其保留信号作频谱图局部放大如图 6(b)所示。从图6可以看出:在频域上轴承外圈故障特征频率12.5 Hz及倍频非常明显,压缩感知信号有效地保留了原信号的故障信息,体现了本文方法的有效性。 图6 压缩感知重构信号的包络及其频谱Fig. 6 Envelope curve and frequency spectrum of signal reconstruction 1) 从信号稀疏分解的角度出发,结合分块阈值自适应降噪方法,提出了稀疏度控制因子,解决了提升小波分解中滤波器选择和最佳分解层数的难题。 2) 以利用观测次数下限为指导,结合提升小波多尺度分解特性,自适应确定提升小波各节点的观测数,在减少观测数据量的同时,提高了重构的速度和精度。 3) 仿真信号和实测信号验证了本文方法的有效性以及良好的抗噪性能,在机械状态监测和数据通讯等领域具有广阔的应用前景。 [1] 戴琼海, 付长军, 季向阳. 压缩感知研究[J]. 计算机学报, 2011, 34(3): 425−435. DAI Qionghai, FU Changjun, JI Xiangyang. Research on compressed sensing[J]. Chinese Journal of Computers, 2011, 34(3): 425−435. [2] DONOHO D, TSAIG Y. Extensions of compressed sensing[J]. Signal Processing, 2006, 86(3): 533−548. [3] 郭海燕, 王天荆, 杨震. DCT域的语音信号自适应压缩感知[J]. 仪器仪表学报, 2010, 31(6): 1262−1268. GUO Haiyan, WANG Tianjing, YANG Zhen. Adaptive speech compressed sensing in the DCT domain[J]. Chinese Journal of Scientific Instrument, 2010, 31(6): 1262−1268. [4] 王伟伟, 廖桂生, 吴孙勇, 等. 基于小波稀疏表示的压缩感知SAR成像算法研究[J]. 电子与信息学报, 2011, 33(6): 1440−1447. WANG Weiwei, LIAO Guisheng, WU Sunyong, et al. A compressive sensing imagine approach based on wavelet sparse representation[J]. Journal of Electronics and Information Technology, 2011, 33(6): 1440−1447. [5] 罗武骏, 陶文凤, 左加阔, 等. 自适应语音压缩感知方法[J].东南大学学报(自然科学版), 2012,42(6): 1027−1031. LUO Wujun, TAO Wenfeng, ZUO Jiakuo, et al. Adaptive compressed sensing method for speech[J]. Journal of Southeast University (Natural Science Edition), 2012, 42(6): 1027−1031. [6] 王楠, 孟庆丰, 郑斌. 振动信号无线传输的数据压缩编码算法[J]. 振动、测试与诊断, 2013, 33(2): 236−241. WANG Nan, MENG Qingfeng, ZHENG Bin. Data compression and coding algorithm used in wireless transmission of vibration signal[J]. Journal of Vibration, Measurement & Diagnosis, 2013, 33(2): 236−241. [7] 孙林慧, 杨震, 叶蕾. 基于自适应多尺度压缩感知的语音压缩与重构[J]. 电子学报, 2011, 39(1): 40−46. SUN Linhui, YANG Zhen, YE Lei. Speech compression and reconstruction based on adaptive multiscale compressed sensing theory[J]. Acta Electronica Sinica, 2011, 39(1): 40−46. [8] 季忠, 黄捷, 秦树人. 提升小波在齿轮箱故障诊断中的应用[J]. 振动、测试与诊断, 2010, 30(3): 291−294. JI Zhong, HUANG Jie, QIN Shuren. Application of gear box fault diagnosis based on lifting wavelet transform[J]. Journal of Vibration, Measurement & Diagnosis, 2010, 30(3): 291−294. [9] LI Linyuan. On the block thresholding wavelet estimators with censored data[J]. Journal of Multivariate Analysis, 2008, 99(8): 1518−1543. [10] BARANIUK R G. Compressive sensing[J]. IEEE Signal Processing Magazine, 2007, 24(4): 118−121. [11] 吴光文, 张爱军, 王昌明. 一种用于压缩感知的投影矩阵优化算法[J]. 电子与信息学报, 2015, 37(7): 1681−1687. WU Guangwen, ZHANG Aijun, WANG Changming. Novel optimization method for projection matrix in compress sensing theory[J]. Journal of Electronics & Information Technology, 2015, 37(7): 1681−1687. [12] 荆楠, 毕卫红, 胡正平, 等. 动态压缩感知综述[J]. 自动化学报, 2015, 41(1): 22−37. JING Nan, BI Weihong, HU Zhengping, et al. A survey on dynamic compressed sensing[J]. Acta Automatica Sinica, 2015, 41(1): 22−37. [13] MARK A D. Random observations on random observations: sparse signal acquisition and processing[D]. Houston: Rice University. School of Electrical and Computer Engineering, 2010: 29−99. (编辑 赵俊) Adaptive compressed sensing of machinery vibration based on lifting wavelet transform WANG Huaiguang, ZHANG Peilin, WU Dinghai, FAN Hongbo In order to solve the problem of mass data acquisition and transmission of complicated equipment condition monitoring, a method of adaptive compressed sensing of machinery vibration based on lifting wavelet transform was put forward. Taking account of optimal parameters selection problem of lifting wavelet signal process, the lifting wavelet filter and layer numbers were optimally chosen by considering the factor of sparseness, then combined with block threshold noise reduction method to implement the sparseness decomposition of machinery vibration signal. Based on the block compressed sensing and the least quantity of measured data, which satisfy the restricted isometry property, the problem of measured data quantity of node signal based on lifting wavelet transform was solved, and the machine condition monitoring system of adaptive compressed sensing based on lifting wavelet transform was built. The results show that the proposed method can reduce the quantity of measured data and enhance the reconstruction speed and performance. adaptive compressed sensing; sparseness; lifting wavelet transform; data compression; machinery vibration; condition monitoring TN919.3;TP277;TN911.72 A 1672−7207(2016)03−0771−06 10.11817/j.issn.1672-7207.2016.03.009 2015−03−06; 2015−06−20 国家自然科学基金资助项目(51305454) (Project(51305454) supported by the National Natural Science Foundation of China) 张培林,博士,教授,博士生导师,从事机械维修理论与技术的研究;E-mail: ZPL1955@163.com
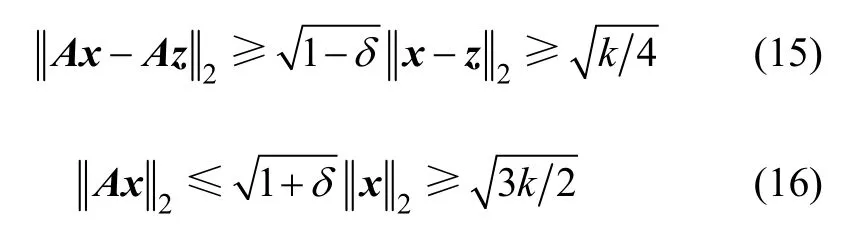


3 计算结果分析






4 结论
(Department of Vehicle and Electrical Engineering, Ordnance Engineering College, Shijiazhuang 050003, China)

