基于Bootstrap技术的相干信源数估计

刘鲁涛，冯凯

(哈尔滨工程大学 信息与通信工程学院，黑龙江 哈尔滨，150001)

基于Bootstrap技术的相干信源数估计

刘鲁涛，冯凯

(哈尔滨工程大学 信息与通信工程学院，黑龙江 哈尔滨，150001)

针对信号源相干的问题，采用空间平滑技术对信号源去相关得到等效协方差矩阵，提出2种信源数检测的方法，一种是基于等效协方差矩阵特征值的一系列假设检验，另一种是将等效阵列信号协方差矩阵分别投影到信号的特征子空间和噪声的特征子空间，以特征空间投影为基础的假设检验。数据的分布未知，并且应用Bootstrap方法估计零假设下提出的检测统计量的分布。通过信噪比(RSN)、快拍数、角度分辨率变化等情况下的仿真，验证所提方法的有效性。研究结果表明：所提算法在低信噪比及小样本数量的情况下，性能比其他算法的性能好。

相干源；空间平滑；Bootstrap；假设检验

空间谱估计在许多应用领域有着重要作用。信源数检测作为信号参数估计的先决条件，是空间谱估计中的热点问题。近年来，空间谱估计研究领域取得了快速的发展，大量改进算法丰富了子空间类算法[1−3]。但信源在多径传播和复杂电磁干扰的背景下，会产生大量的相干和强相关信号，相干源个数估计是信源数检测问题中的难点。目前，针对信源的解相干问题相关学者提出不少算法[4−8]，最为常见的为空间平滑及其改进算法。近几年来提出了不少利用Toeplitz矩阵的结构特点来构造数据矩阵的算法：梁浩等[5]采用垂直放置的L型阵列，通过对重构的Toeplitz矩阵进行特征分解，得到对应的噪声子空间；甄佳奇等[6]针对大多数解相干算法只能应用线阵而不能应用于均匀圆阵，利用空间差分方法和矩阵重构相结合来估计相干信号；闫康等[7]提出基于面阵的相干信源解相干问题，利用矩阵重构降低相干源对阵列协方差矩阵的秩的影响；王凌等[8]利用阵列接收数据之间的互相关信息，构造出2个Toeplitz矩阵形式的等效协方差矩阵，通过对新矩阵做一次特征值分解，即可实现解相干；毛维平等[9]沿轴向对阵列进行虚拟平移，利用空间平滑技术处理数据以恢复协方差矩阵的秩，实现相干信号解相干。在许多实际系统中，高斯数据和大样本数量的假设无法满足，GU等[10]提出了一种基于假设检验的替代方法，首先通过空间平滑对信号源去相关，然后进行假设检验。本文作者同样对信号源采用空间平滑技术去除相关性，得到等效协方差矩阵，对等效协方差矩阵进行变换，得到不同的变量，分别进行假设检验。在零假设下检验统计量的分布使用Bootstrap方法来估计[11−12]，这种方法对高斯分布和大部分非高斯分布均有效。因此，新方法的优点是可以解决不满足高斯分布和渐进条件下的问题。

1　数据模型

考虑N个远场窄带信号，入射到M维空间均匀线阵，d=λ/2，且入射方向为。假设M＞N，信源数N为未知估计量，从传感器阵列接收的快拍数为L的零均值数据[13]表示为

式中：(⋅)H为矩阵的共轭转置算子；I为单位矩阵。

信号和噪声假设是不相关的，且各自分布未知，阵列协方差矩阵为

2　空间平滑技术去相关

空间平滑算法在一般情况下只适合于均匀线阵，应用在相干信号或相关性较强的信号去相关性时效果较好。空间平滑算法主要是把线阵分割为彼此重叠的几个子阵列，它们有着相同的阵列流型，再把所有子阵列的协方差矩阵求平均，就可以去除信号的相干性。

2.1前向平滑

空间平滑算法将其均匀分为相互交错的p个子阵，每个子阵的阵元数为m，即M=m+p−1，对每个子阵列逐步地右移，每个子阵列的输出矢量表示为

若子阵列阵元数m＞N，子阵列数p≥N，则可将N个相干信源转变为N个独立信源。此时，有效阵元数将减少至m。

2.2前后向平滑

得后向平滑的信号协方差矩阵Rb[14]为

前后向平滑处理后，阵列协方差矩阵等效为

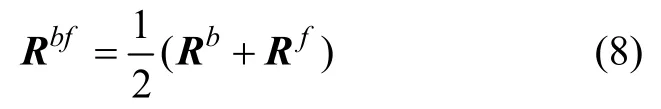
式中：Rbf为前后平滑后的等效协方差矩阵。N个信号源，其中有J个相干源，最小的子阵列数p≥J/2，可将平滑协方差矩阵的秩恢复为N，此时，最小阵列数为Mmin=p+N≥J/2+N 。对相关信源去相关后，可对信号进行准确的信源个数估计。

3　相干源算法估计原理

3.1基于特征值的假设检验

对等效协方差矩阵做特征值分解得

最小的mN−个特征值代表了噪声空间，只需同时检验对应于噪声空间的特征值，就可推导出信源数N。这个过程可被描述为

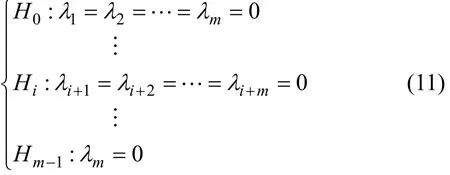
检验应从H0开始，若H0被接受，则意味着，没有信号源存在，即信号源数N=0，若H0被拒绝，则相对的被接受，意味着至少存在1个信号，然而没有具体信息能够说明存在信号数量。因此，通过逐步检验假设Hi，最大的特征值的作用被减小。当某一假设成立或达Hm−1时，检验停止。对于给定的显著水平α，当没有信号存在时，正确检验出N=0的概率被维持在1−α。因此，每个假设都在全局显著水平α下被检验。为进行式(11)的假设检验，给出检验统计量Ei为

检验统计量为特征值算术均值和几何均值的差异，在实际中，若所有的特征值对应于噪声空间，则检验统计量将非常小，甚至接近于0，否则将较大。

3.2Bootstrap对渐进分布的估计

进行假设检验的显著度估计需要检验统计量零假设下的分布知识，用Bootstrap技术来进行空域下的非参数估计[14]。Bootstrap技术由EFORN等[15]在使用传统方法计算置信区间失效时引入，近年来该方法在信源数检测方面颇受关注，其主要采用有放回的重采样方法计算变量的统计特性，使一组样本变为多组样本，相当于增大了样本容量，这样可充分利用样本信息，利用现在样本来模拟总体分布，避免了对数据分布做出假设。Bootstrap技术重采样数据集进行推理，避免了在小样本情况下渐进分布估计的错误。其核心步骤是：先建立样本集，再重采样得到Bootstrap数据集，执行检验推理。本节给出EBS(基于特征值的假设检验)方法，该方法应用特征值构造新的检测统计量Ei，从而形成一些列的假设检验来检测信源数。

将阵列快拍数据收集到1个数据阵列中，即

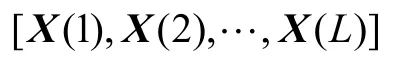
在原始数据中随机抽取阵列快拍，作为新的快拍数据，每个快拍被抽取到的概率相同，为1/L，新的Bootstrap数据阵列为

通过B次Bootstrap方法重采样得到B个重采样样本，第b个重采样样本为。分别计算数据()tX得到检验统计量Ei和重采样样本的检验统计量，文献[15−16]阐述了零假设下的检验统计量Ei的经验分布估计为

文献[15−16]中假设检验的显著度定义为

但形势很快逆转。2009年元旦，程晓带方勋梅去海螺沟疯玩了一天回来，程晓要送她回家，方勋梅娇嗔道：“不呢，今晚你住哪我住哪！”程晓无法拒绝，战战兢兢地将女友带到了自己的蜗居。

式中：()I⋅为指示函数。假设，显著水平为α，从i=0开始，若eiPα≥则Hi被接受，否则，设1ii=+ 并且重复检验。可以认为显著水平α为调整参数，当没有信号存在时，α维持在很小的数值(一般小于5%)以减少错误检测概率。在小样本数、高信噪比或弱相关等理想情况下，通过减小α，能增大Bootstrap检测的概率[16]。

3.3基于特征投影的假设检验信源数估计方法

Rbf的m−N个最小的特征值是噪声方差的估计值，由式(3)得

由于信号特征子空间与导向矢量在同一空间内，对应的投影的模|pki|应为相对较大的值。由于特征子空间与导向矢量正交，对应的投影pki的模在理论上为0，而实际上常为相对较小的值。投影还可以表示为

由式(19)可知：Rbf在U的投影为UΗ，因此，可用U估计目标数。ui表示为。UΗ第 k行元素模的均值为

显著水平与式(11)的α相同，与式(12)相似，使用如下的检测统计量Vi：

若特征矢量对应噪声空间，则检测统计量Vi接近0。本节给出基于特征投影的假设检验信源数估计方法，PBS(基于特征投影的假设检验)方法，与前文EBS方法不同之处在于，这里的检测统计量是基于特征投影形成的。与前文提到的B次Bootstrap方法重采样得到B个重采样样本相同，第b个重采样样本为。分别计算数据X(t)得到检验统计量Vi和重采样样本的检验统计量，Vi的分布估计为

与式(14)类似，假设检验的显著度viP定义为

从i=0开始，若eiPα≥，则Hi被接受，否则，设i=i+1并且重复检验。

4　仿真结果

利用计算机仿真试验来进行算法的性能分析、比较、并验证算法的有效性。考虑线性均匀阵列，阵元数M=8，快拍数L=100，2个等功率相干的信号分别从10°和24°的方向辐射到阵列上，重采样次数B=100，检验显著度为α=2%，M个阵元噪声之间相互独立，信噪比定义为RSN=10lg(Ps/Pn)，Ps为信号功率，Pn为噪声功率，蒙特卡洛实验次数为1 000次。对阵列协方差矩阵空间平滑处理去相关时，子阵列的阵元数为m=5，将基于特征值的假设检验方法简称为EBS，将基于特征投影的假设检验方法称为PBS，与信息论准则(MDL)、盖世圆的方法[17](GDE)和同类Bootstrap方法的T2检测器(简称为BBS)对比[18]。取盖氏圆方法中的D(L)=0.05。

图1所示为在空间相干高斯信号和空间均匀高斯噪声的条件下，检测器性能与信噪比的关系对比图。信噪比从−15 dB变化到20 dB，快拍数为100。由图1可以看出：进行去相关处理后再进行信源数估计，得到的效果较理想。EBS和PBS方法性能优于其他算法性能，EBS算法性能最优。在低信噪比下，基于Bootstrap技术的算法检测性能明显高于其他算法的性能。在高信噪比的条件下，EBS和PBS算法的正确检测概率接近100%。

图1　高斯数据下改变RSN的检测器正确检测概率Fig. 1 High detecting probability of detection at different RSNwith Gaussian data

图2所示为本文所提出方法在信源功率不相等的情况下的检测性能。信号源为分别从10°和24°入射到阵列上的2个相干高斯信号，从10°入射的信号的信噪比为0 dB，从24°入射的信号的信噪比为0～10 dB，噪声为空间均匀高斯噪声，其他条件不变。由图2可以看出：当信噪比的差异大于5 dB时，检测器的性能开始下降，但EBS算法性能仍优于其他算法的性能；当信噪比差达10 dB时，EBS算法的正确检测概率仍能到达70%。信源信噪比不同对GDE算法和MDL准则影响较大。

图3所示为高斯数据下改变快拍数的检测器性能，其中相干信号源功率相等，为0 dB，快拍数从20个变化到300个。由图3可以看出：随着快拍数的提高，检测器的性能得到提高。当快拍数为20～100 时，基于Bootstrap技术的3种检测器(BBS，EBS和PBS算法)的检测性能均高于MDL和GDE方法的性能。这说明基于Bootstrap技术的算法在小快拍数的情况下性能优于其他算法的性能，其中EBS算法性能最优。

图4所示为角度分辨率对检测器性能的影响，其中信噪比为10 dB，快拍数为100个。2个相干信号源，一个从10°入射到阵列上，另一个的入射方向从10°变化到24°。从图4可以看出：检测性能随着角度分辨率的增加而提高，基于Bootstrap技术的检测器的角度分辨率优于其他算法的分辨率，其中EBS的最优。在高角度分辨率时，EBS和PBS方法的检测器性能到达100%，是一致估计，但是BBS不是一致估计。

图2　信源功率不相等情况下的检测器正确检测概率Fig. 2 High detecting probability of detection at different source powers

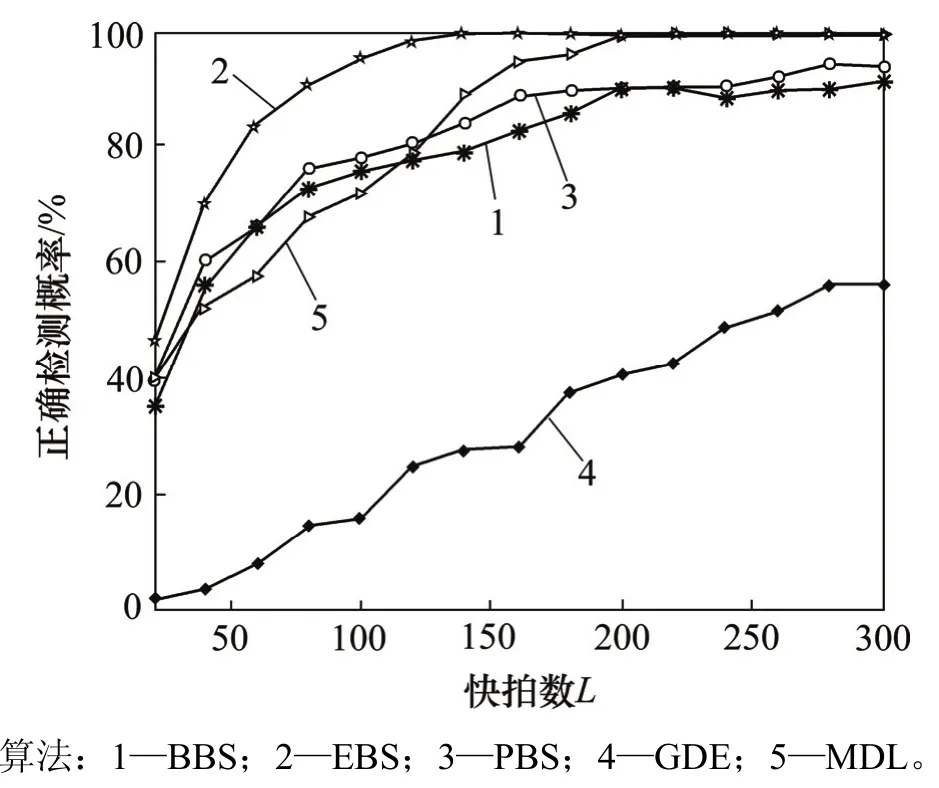
图3　高斯数据下改变快拍数的检测器正确检测概率Fig. 3 High detecting probability of detection at different numbers of snapshots with Gaussian data

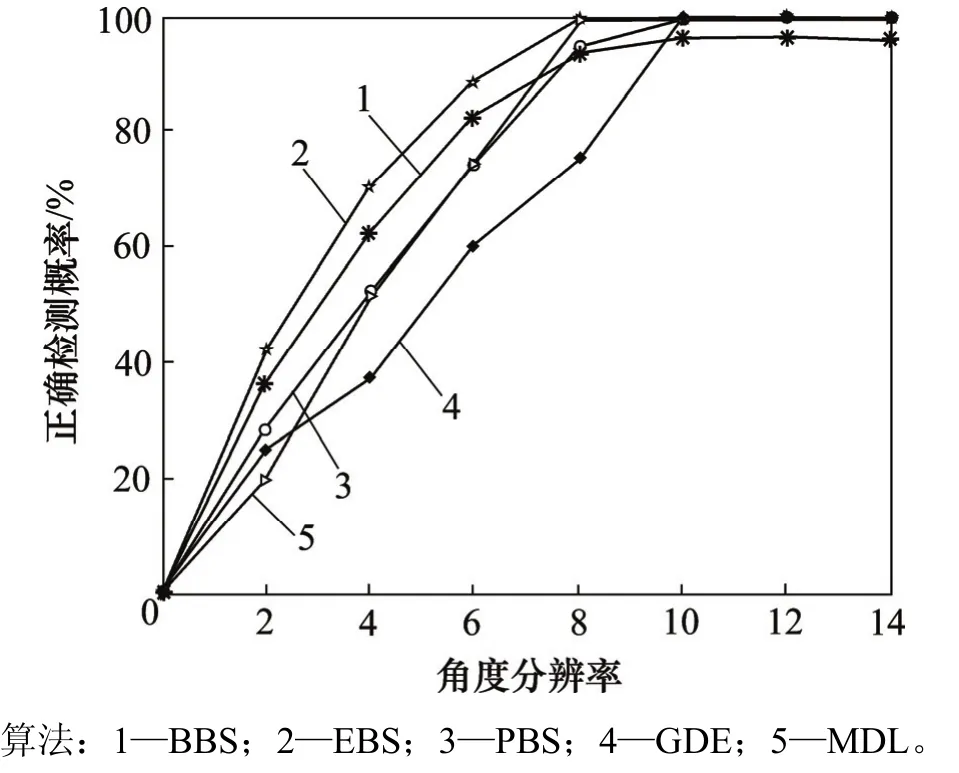
图4 高斯数据下改变角度分辨率的检测器正确检测概率Fig. 4 High detecting probability of detection at different angular resolutions with Gaussian data

图5所示为拉普拉斯信号下改变信噪比的检测器性能，其中相干信号源为拉普拉斯信号，噪声为空间均匀高斯噪声。图6所示为拉普拉斯噪声下改变信噪比的检测器性能，其中相干信号源为高斯信号，噪声为空间均匀拉普拉斯噪声。2个等功率相干的信号分别从10°和24°的方向辐射到阵列上，快拍数为100个，信号信噪比从−15 dB变化到20 dB。信息论准则是在高斯数据假设下的一致估计。如前文提到的，Bootstrap技术对数据分布做出估计时，不需要对数据分布做出假设，所以当信号源或者噪声不满足高斯分布时，基于Bootstrap技术的检测方法仍然有效。由图5和图6可知：基于Bootstrap技术的检测器性能同高斯数据的情况下相似，说明检测器的鲁棒性。

图7所示为不同显著水平α下的检测概率。显著水平α被认为是一个调整参数。当没有信号存在时，α维持在很小的数值以减少错误检测概率。从图7可以看出：在相同条件下，α=5%的错误检测概率比α=2%时的低，但减少的幅度并不显著。所以，通常情况下α的取值一般小于5%即可。但随着显著水平α的降低，需更多的重采样样本来进行估计，并且计算量增加。

图8所示为重采样数B对检测器性能的影响。以EBS检测器为例，分别实验在B=50，200和1 000情况下的EBS检测器性能。从图8可以看出：随着重采样数B的增多，检测器性能得到改善，但是改善不显著。这是因为重采样数越多，相当于样本数量越大，对检测统计量分布的估计越准确。但重采样数的提高同时也增大了计算量，B越大，所需计算时间越长。B=1 000的计算时间基本为B=200时的4倍。一般情况下，B的取值范围为50～200，同时满足计算时间和分布估计准确性的要求。

图5　拉普拉斯信号下改变RSN的检测器正确检测概率Fig. 5 High detecting probability of detection at different RSNwith Laplacian signals

图6　拉普拉斯噪声下改变RSN的检测器正确检测概率Fig. 6 High detecting probability of detection at different RSNwith Laplacian noise

图7　不同α的检测器正确检测概率Fig. 7 High detecting probability of detection with differentα

图8　不同B下检测器正确检测概率Fig. 8 High detecting probability of detection with different B

5　结论

1) 所提出的假设检验统计量在空域下的分布用Bootstrap方法进行估计。仿真结果表明，所提出的算法在小样本数量的情况下，性能优异。

2) 当数据为非高斯数据、低信噪比、信源功率不相同等不理想的条件下，所提出的算法仍然有效。因此，在相干信源数估计问题中，提出的检测模型性能优于其他算法的性能。

[1] 王鼎, 吴瑛. 多子阵互耦影响下的鲁棒自校正算法[J]. 系统工程与电子技术, 2011, 33(6): 1204−1211. WANG Ding, WU Ying. Robust self-calibration algorithm for multiple subarrays in presence of mutual coupling[J]. Systems Engineering and Electronics, 2011, 33(6): 1204−1211.

[2] 胡增辉, 朱炬波, 何峰, 等. 互耦条件下均匀线阵DOA盲估计[J]. 电子与信息学报, 2012, 34(2): 382−387. HU Zenghui, ZHU Jubo, HE Feng, et al. Blind DOA estimation in the presence of mutual coupling using uniform linear array[J]. Journal of Electronics & Information Technology, 2012, 34(2): 382−387.

[3] 刘俊, 刘峥, 谢荣, 等. 互耦条件下米波雷达角度估计的自校正算法[J]. 电波科学学报, 2011, 26(6): 1046−1051. LIU Jun, LIU Zheng, XIE Rong, et al. Auto-calibration angle estimation algorithm for VHF radar in the presence of mutual coupling[J]. Chinese Journal of Radio Science, 2011, 26(6): 1046−1051.

[4] 徐友根, 刘志文. 修正的虚拟空间平滑算法[J]. 电子学报, 2009, 37(12): 2646−2650. XU Yougen, LIU Zhiwen. Modified virtual spatial smoothing algorithm[J]. Acta Electronica Sinica, 2009, 37(12): 2646−2650.

[5] 梁浩, 李小波. 基于Toeplitz矩阵重构的相干信源二维DOA估计算法[J]. 电子信息对抗技术, 2012, 27(1): 23−26. LIANG Hao, LI Xiaobo. Two-dimensional DOA estimation of coherent signals based on the Toeplitz matrix reconstruction[J]. Electronic Information Warfare Technology, 2012, 27(1): 23−26.

[6] 甄佳奇, 丁群, 赵冰. 虚拟阵列下的相干信号测向算法[J]. 系统工程与电子技术, 2013, 35(10): 2032−2036. ZHEN Jiaqi, DING Qun, ZHAO Bing. Direction finding algorithm for coherent signals by virtual array[J]. Systems Engineering and Electronics, 2013, 35(10): 2032−2036.

[7] 闫康, 孙志刚, 郭肃丽. 一种基于面阵的相干信源DOA估计算法[J]. 无线电工程, 2013, 43(10): 22−24. YAN Kang, SUN Zhigang, GUO Suli. An algorithm of direction of arrival estimation for plane array with coherent signal source[J]. Radio Engineering, 2013, 43(10): 22−24.

[8] 王凌, 李国林, 刘坚强, 等. 一种基于数据矩阵重构的相干信源二维测向新方法[J]. 西安电子科技大学学报, 2013, 40(2): 130−137. WANG Ling, LI Guolin, LIU Jianqiang, et al. New method for estimating 2-D DOA in the coherent source environment based on data matrix reconstruction[J]. Journal of Xidian University, 2013, 40(2): 130−137.

[9] 毛维平, 李国林, 谢鑫. 均匀圆阵相干信源二维波达方向估计[J]. 系统工程与电子技术, 2013, 35(8): 1596−1601. MAO Weiping, LI Guolin, XIE Xin. 2D-DOA estimation of coherent signals based on uniform circular array[J]. Systems Engineering and Electronics, 2013, 35(8): 1596−1601.

[10] GU J F, WEI P, TAI H M. Detection of the number of sources at low signal-to-noise ratio[J]. IET Signal Processing, 2007, 1(1): 2−8.

[11] ZOUBIR A, BOASHASH B. The bootstrap and its application in signal processing[J]. IEEE Signal Processing Magazine, 1998, 15(1): 56−76.

[12] POLITIS D. Computer-intensive methods in statistical analysis[J]. IEEE Signal Processing Magazine, 1998, 15(1): 39−55.

[13] 黄可生, 黄干涛, 周一宇. 基于协方差矩阵变换的相干源个数估计[J]. 信号处理, 2003, 19(5): 390−394. HUANG Kesheng, HUANG Gantao, ZHOU Yiyu. Determining the number of coherent signal based on covariance matrix transforming[J]. Signal Processing, 2003, 19(5): 390−394.

[14] ZOUBIR A, ISKANDER D. Bootstrap techniques for signal processing[M]. Cambridge: Cambridge University Press, 2004: 119−129.

[15] EFORN B, TIBSHIRANI R. An introduction to the bootstrap[M]. London: Chapman & Hall, 1993: 124−139.

[16] BRCICH R, ZOUBIR A, PELIN P. Detection of sources using bootstrap techniques[J]. IEEE Transactions on Signal Processing, 2002, 50(2): 206−215.

[17] WU H T, YANG J F, CHEN F K. Source number estimators using transformed Gerschgorin radii[J]. IEEE Transactions on Signal Processing, 1995, 43(6): 1325−1333.

[18] AOUADA S, TRANSKOV D, HEUREUSE N, et al. Application of the bootstrap to source detection in nonuniform noise[C]// IEEE International Conference on Acoustics, Speech and Signal Processing. Pennsylvania, USA: IEEE, 2005: 997−1000.

(编辑 刘锦伟)

Coherent source signal detection using Bootstrap technique

LIU Lutao, FENG Kai
(School of Information and Telecommunication, Harbin Engineering University, Harbin 150001, China)

The spatial smoothing technology was used to get rid of signals’ coherent, and the equivalent covariance matrix was obtained. Two approaches based on Bootstrap technique were proposed for developing source number detection methods. One method formulated a sequential hypothesis testing based on the eigenvalues of the equivalent covariance matrix. The other source method was a hypothesis testing based on eigen-space projection, whose equivalent array signal covariance matrix was projected from signal subspace to noise subspace. As no assumption was made on the distribution of the data, the Bootstrap was used to estimate the distribution at the null of the proposed test statistics. Through the simulations of different signal-to-noise ratio (RSN), the numbers of snapshots and angular resolutions, it is found that the performances of the proposed methods are effective and superior to those of the existing methods in the low signal-to-noise ratio (RSN) and small snapshots.

coherent signal; spatial smoothing; Bootstrap; hypothesis testing

TN911.23

A

1672−7207(2016)03−0793−07

10.11817/j.issn.1672-7207.2016.03.012

2015−03−16；

2015−05−23

国家自然科学基金资助项目(61201410) (Project(61201410) supported by the National Natural Science Foundation of China)

刘鲁涛，博士，副教授，从事宽带信号处理、检测与识别研究；E-mail: liulutao@msn.com