无源时间反转聚焦方法

刘伟，付永庆，许达

(1. 哈尔滨工程大学 信息与通信工程学院，黑龙江 哈尔滨，150001；2. 哈尔滨工程大学 水声工程学院，黑龙江 哈尔滨，150001)

无源时间反转聚焦方法

刘伟1，付永庆1，许达2

(1. 哈尔滨工程大学 信息与通信工程学院，黑龙江 哈尔滨，150001；2. 哈尔滨工程大学 水声工程学院，黑龙江 哈尔滨，150001)

为了提高时间反转聚焦方法在电子战中的适用性，提出一种基于电磁波波动方程的无源时间反转聚焦方法。该方法以平面电磁波波动方程的时间反转不变性为基础，利用时间反转阵列接收并记录一段时间的信源发射信号，然后对该信号进行时间反转处理，利用计算已知目标域内各观测点处的虚拟接收和信号及其能量代替时间反转后信号的物理传输过程，实现时间反转后信号在信源处的重聚焦，其中能量最大点所对应的观测点即为信源点。在理论上验证该方法的正确性，然后以均匀圆形时间反转阵列为例进行仿真实验。研究结果表明：该无源时间反转聚焦算法具有有效性和准确性，在低信噪比下具有良好聚焦性能。

无源时间反转；波动方程；聚焦；观测点

时间反转由光学中的相位共轭引申而来，FINK等[1]提出并验证了时间反转技术在超声实验中的有效性，随后SONG等[2]对该技术在海洋实验中的应用进行了研究，直到2004年，时间反转开始被引入到电磁领域[3]。到目前为止，时间反转技术已经在超声碎石[4]、无损探伤[5]、目标探测[6−8]、无线通信[9−10]、成像[11−12]和雷达[13−14]等领域得到广泛研究。其基本原理为：收发合置的传感器阵列接收辐射源发射的信号并对该信号进行时间反转，然后将时间反转后的信号物理发射到空间中，则经过反向物理传输，时间反转后信号会在信源处实现重聚焦[15]。从以上原理可以看出：经典时间反转理论需要将时间反转后信号进行物理传输，并在信源处设置观察阵列来实现信号重聚焦，不能直接用于实际电子战中。水声领域提出了一种虚拟时间反转镜来实现对辐射源目标的被动检测[16]，但该方法需要预先对信道的冲击响应函数进行估计，不适合用于复杂多变的电子战环境。为了解决以上问题，本文作者提出了一种无源时间反转聚焦方法，该方法只利用接收阵列接收一段信源的发射信号，接着将该信号进行时间反转处理，然后利用时间反转后信号计算已知目标域中各观测点的虚拟接收和信号及其能量，即可实现在信源处的信号重聚焦。以平面电磁波波动方程为基础，从理论上分析了无源时间反转聚焦方法的正确性，并给出了算法步骤，最后以均匀圆形时间反转阵列为例，验证了该算法的有效性。

1　波动方程的时间反转不变性

时间反转在时域中是对信号的一种逆序操作，即将信号在时序上进行反转，在频域内可等效为相位共轭。以波动方程的时间反转不变性为基础，把接收天线阵列接收到的目标信号进行时间反转处理并重新发射到空间中，则会实现在目标处的信号重聚焦。

假设电磁场中的标量位函数为ϕ(r,t)，则在无源场区域满足的标量波动方程为[17]：

式中：μ和ε分别为介质的介电常数和磁导率；r为电磁波传播的位移矢量。

考虑远场平面电磁波，则式(1)所示标量波动方程的通解为：

式中：f1和f2为任意函数；，为电磁波传播速度。

令

可以看出，式(3)和(4)分别表示传播方向相反的两类波形，并且它们都是波动方程的解。

对式(3)和(4)进行时间反转处理，可得：

可见，ϕ1(r,−t)与ϕ2(r,−t)也是波动方程的解，因此，波动方程具有时间反转不变性。这一特性说明由目标激励的每一个电磁波，经过介质传播之后的场，必定会存在一个时间上与之相反的场沿着相同的路径返回到目标的位置，实现电磁波信号在目标处的聚焦。

2　无源时间反转聚焦方法

2.1时间反转聚焦原理

时间反转镜(time reversal mirror, TRM)阵列将接收到的信号进行时间反转，然后重新发射到空间中，反向传输的时间反转信号就会实现在信源处的重聚焦，其原理如图1所示。

图1　时间反转聚焦模型Fig. 1 Model of time reversal focusing

令用()Sω为信号频谱，()Hω为信道的传输函数，则信号经过信道传输，到达TRM接收阵列时的频谱可以表示为

时域内的时间反转在频域内表示为复共轭，令RTR(ω)是R(ω)的复共轭，即

将时间反转后信号反向发射，并按原信道进行反向传输可得到：

式中：H∗(ω)H(ω)为实、偶、正函数，它在时间零点的傅里叶变换同相相加，得到最大值，实现信号重聚焦[18]。

2.2无源时间反转聚焦算法

假设图1中TRM阵列由N个天线阵元组成，且信源的发射信号为s(t)。定义信源与TRM阵列中第n个阵元天线的冲激响应函数为hn( rn, t)(其中：1≤n≤N，rn为信源与第n个阵元之间的传输距离)。因此，第n个阵元天线接收到的信号为[19]

写成频域形式为

对各阵元的接收信号在时域上进行时间反转，相当于对其频域信号进行相位共轭，于是第n个阵元天线的时间反转后信号可以表示为

根据图1所示的时间反转聚焦原理，若想实现信号在信源处的重聚焦，需要将间反转后信号进行反向物理传输至目标域，并在目标域设置接收阵列以观察时间反转聚焦现象。但在非合作信源情况下(如敌方雷达或通信电台等)，实现时间反转后信号的反向物理传输是没有意义的。因此，为了解决非合作信源情况下的时间反转聚焦问题，可将已知目标域平均划分成M个观测点，并利用观测点与各天线阵元之间的相对位置来计算各观测点处的虚拟接收和信号来实现时间反转聚焦。

令目标域中第k (1≤k≤M)个观测点与第n个阵元天线之间的传输函数为Hkn(rkn,ω)，其中，rkn为第k个观测点与第n个阵元之间的传输距离，则可通过计算得到目标域中第k个观测点处虚拟接收到的第n个阵元反向传输的信号为

由式(21)可知：第n个接收天线的时间反转信号达到最大值的时间仅与信源的发射信号有关，且各天线阵元的时间反转信号达到最大值的时间相同，都是在观测点与信源点重合时达到最大值，即在信源处获得重聚焦。因此可通过计算目标域中各观测点处虚拟接收到的N个天线阵元时间反转信号的和信号的能量值来实现在信源处的重聚焦，其中最大能量点所对应的观测点即为信源点。

由电磁平面波的波动方程的解可将目标与TRM阵列中第n个阵元天线的冲激响应函数写为以下形式：

计算目标域中所有观测点的信号能量，其中能量最大值所对应的观测点即为目标信源点。因此，通过计算目标域中各观测点的信号能量值，即可实现时间反转信号在目标处的重聚焦。

通过以上分析可将无源时间反转聚焦算法分为以下步骤：

1) 利用TRM阵列接收并记录一段时间为T的信源发射信号；

2) 将接收信号进行时间反转处理；

3) 确定已知目标搜索域中各目标观测点位置；

4) 通过计算得到各目标观测点的虚拟接收和信号；

5) 计算各观测点的信号能量，实现在信源处的信号重聚焦。

3　仿真分析

考虑图2所示均匀圆形时间反转阵列，忽略其相干性，通道不一致性等，其中N个天线阵元均匀分布在半径为r的圆周上，阵列的几何中心与坐标原点重合。为实现无源时间反转聚焦，选取图3所示为目标搜索域，其中M个观测点均匀分布在半径为r′的圆周上，且每个观测点的坐标为Pk( r′,θk)。假设目标位于目标搜索域内且方位角为82°，目标信源发射频率为10 MHz的正弦电磁波。仿真中取N=10，r=20 m，图4所示为波束指向90°时的时间反转阵列方向图。目标搜索域取r′=20 km，观测点数M=360，即搜索步进为1°，时间反转阵列的信号记录时间为1 ms，则目标域内各观测点的虚拟接收和信号归一化能量值分布如图5所示。从图5可以看出：目标域内的归一化能量值在方位角为82°的观测点处取得最大值，此观测点即为信源点，验证了文中所提无源时间反转聚焦算法的有效性。

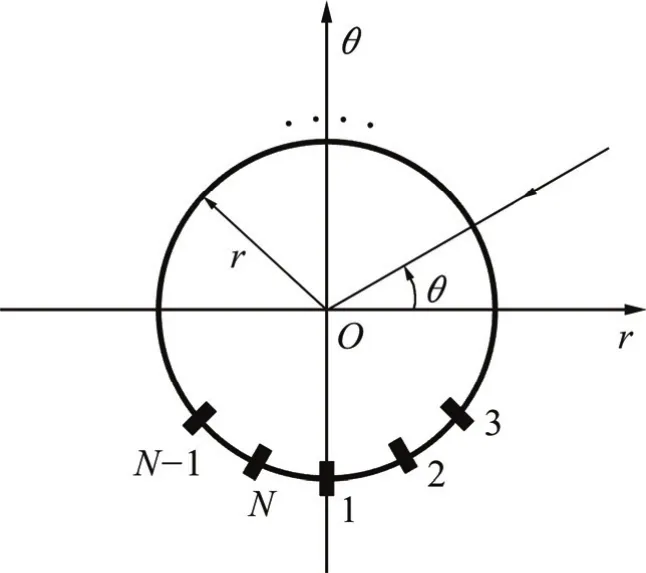
图2　均匀圆形时间反转阵列Fig. 2 Uniform circular time reversal array

图3　目标搜索域Fig. 3 Targets searching area

图4　时间反转阵列方向图Fig. 4 Directivity diagram of time reversal array

图5　目标域内归一化能量值分布Fig. 5 Distribution of normalized energy values in target area

改变时间反转阵列阵元数N，分别取8，10和15，其他参数保持不变。将时间反转阵列接收到的信号进行时间反转，然后计算目标域内各观测点的虚拟接收和信号能量值，图6所示为目标域内各观测点的和信号能量分布情况。从图6可以看出：不同阵元数情况下，无源时间反转聚焦算法都可以有效实现在信源处的信号重聚焦，聚焦方位为82°，而且阵元数越大，信源处的聚焦峰值也越大，这说明阵元数增加可以增强无源时间反转算法在目标处的聚焦效果。

为观察噪声对无源时间反转聚焦算法的影响，在仿真中加入信噪比不同的高斯白噪声，其中时间反转阵列的阵元数N分别取8,10和15，其他参数保持不变，算法时间反转聚焦的均方根误差eRMSE计算公式为

图6　不同阵元数下的无源时间反转聚焦Fig. 6 Passive time reversal focusing in different numbers of element

式中：L为样本数；Xi为样本点；1≤i≤L；为样本平均值。

图7所示为执行200次蒙特卡洛实验时，不同信噪比情况下无源时间反转聚焦算法的均方根误差。从图7可以看出：随着信噪比和阵元数的增大，该算法聚焦的均方根误差都有逐渐减小的趋势，而且在信噪比为0 dB时，3种情况下的聚焦均方根误差都在0.8°以下，显示了该方法在较低信噪比下的良好聚焦性能。图8所示为阵元数为8的情况下，本文方法与传统MUSIC和RB-MUSIC[20]在不同信噪比下的均方根误差对比曲线。从图8可以看出：文中所给出的无源时间反转算法具有更小的均方根误差，可以获得更好的目标检测性能。

为研究不同搜索步进，即不同观测点数对算法聚焦性能的影响，在信噪比为0 dB的情况下取搜索步进分别为1°，0.5°和0.1°，然后通过计算各观测点处的虚拟接收和信号能量值实现在信源处的信号重聚焦。执行200次蒙特卡洛实验可得不同搜索步进情况下的聚焦均方根误差如表1所示。从表1可以看出：随着搜索步进的减小，即观测点数的增加，3种阵元数情况下的聚焦误差也随之减小，同时，表1也显示出了该无源时间反转聚焦算法在信噪比为0 dB情况下的有效准确聚焦性能。

图7　不同信噪比下的聚焦均方根误差Fig. 7 RMSE of focusing in different SNR

图8　3种方法在不同信噪比下的均方根误差Fig. 8 RMSE of three methods in different SNR

表1　不同搜索步进下的聚焦均方根误差Table 1 RMSE of focusing in different searching steppings

4　结论

1) 提出了一种无源时间反转聚焦方法，该方法不需要进行时间反转后信号的物理传输，也不需要对信道的冲击响应函数进行预先估计，而是通过计算目标域中各观测点处虚拟接收到的N个天线阵元时间反转信号的和信号的能量来实现在信源处的重聚焦，其中最大能量所对应的观测点即为信源点。

2) 本文方法具有有效性，在低信噪比情况下具有良好聚焦性能。

3) 无源时间反转聚焦方法只需要对接收信号进行时间反转处理和虚拟能量计算即可实现聚焦，因此更适合应用于电子战中对敌方辐射源的侦测，也可用于任何需要对目标进行被动检测的应用环境。

[1] FINK M, PRADA C, WU F, et al. Self focusing in inhomogeneous media with time reversal acoustic mirrors[C]// IEEE Ultrasonics Symposium Proceedings. Montreal: IEEE Press, 1989: 681−686.

[2] SONG H C, KUPERMAN W A, HOGKISS W S, et al. Iterative time reversal in the ocean[J]. Journal of the Acoustical Society of America, 1999, 105(6): 3176−3184.

[3] LEROSEY G, de ROSNY J, TOURIN A, et al. Time reversal of electromagnetic waves[J]. Physical Review Letters, 2004, 92 (19): 193904-1−193904-3.

[4] THOMAS J L, FINK M. Self focusing on extended objects with time reversal mirror, application to lithotripsy[C]// IEEE Ultrasonics Symposium Proceedings. Cannes, France: IEEE Press, 1994: 1809−1814.

[5] 赵乃至, 阎石, 齐霁. 基于时间反转法的管道周向裂缝损伤检测[J]. 沈阳建筑大学学报, 2013, 29(1): 44−49. ZHAO Naizhi, YAN Shi, QI Ji. The pipeline circumferential cracks damage detection based on time reversal method[J]. Journal of Shenyang Jianzhu University, 2013, 29(1): 44−49.

[6] 时洁, 杨德森, 时胜国. 基于多途模型匹配的浅海噪声源聚焦定位方法[J]. 电子学报, 2013, 41(3): 575−581. SHI Jie, YANG Desen, SHI Shengguo. Research on noise sound source location method in shallow water based on the multi-path model match[J]. ACTA Electronica Sinica, 2013, 41(3):575−581.

[7] FU Yongqing, JIANG Yulei, LIU Zhanya. Near-field source localization method and application using the time reversal mirror technique[J]. Journal of Electronics (China), 2011, 28(4): 531−538.

[8] 李壮, 乔钢, 王健培, 等. 基于虚拟时间反转镜的短基线定位研究[J]. 应用声学, 2012, 31(4): 256−261. LI Zhuang, QIAO Gang, WANG Jianpei, et al. Short baseline positioning based on virtual time reversal mirror[J]. Applied Acoustics, 2012, 31(4): 256−261.

[9] KHAN W N, ZUBAIR M, WYNE S, et al. Performance evaluation of time-reversal on measured 60 GHz wireless channels[J]. Wireless Personal Communications, 2013, 71(1): 707−701.

[10] CHEN Yan, YANG Yuhan, HAN Feng, et al. Time-reversal wideband communications[J]. IEEE Signal Processing Letters, 2013, 20(12): 1219−1222.

[11] CHOI H, OGAWA Y T, OHGANE T. Time-reversal MUSIC imaging with time-domain gating technique[J]. IEICE Transactions on Communications, 2012, E95-B(7): 2377−2385.

[12] LIU Xiaofei, WANG Bingzhou. Transmitting-mode time reversal imaging using MUSIC algorithm for surveillance in wireless sensor network[J]. IEEE Transactions on Antennas and Propagation, 2012, 60(1): 220−230.

[13] JIN Y W, JOSE M F M, NICHOLAS O D. Time reversal in multiple-input multiple-output radar[J]. IEEE Journal of Selected Topics in Signal Processing, 2010, 4(1): 210−225.

[14] FOROOZAN F, ASIF A, JIN Y W, et al. Direction finding algorithms for time reversal MIMO radars[C]// IEEE Workshop on Statistical Signal Processing. Nice: IEEE Press, 2011: 433−436.

[15] FINK M. Time-reversed acoustics[J]. Reports on Progress in Physics, 2000, 63(5): 91−97.

[16] 殷敬伟, 惠俊英. 虚拟时间反转镜技术 [C]// 全国水声学学术会议论文集. 福建: 中国声学学会, 2005: 98−100. YIN Jingwei, HUI Junying. The technique of virtual time reversal mirror[C]// Underwater Acoustics Conference Proceedings. Fujian: China Acoustics Institute, 2005: 98−100.

[17] 谭思浩. 基于时间反转电磁场逆的超宽带雷达成像算法研究[D]. 南昌: 南昌大学物理系, 2013: 38−41. TAN Sihao. Research on ultrawideband radar imaging algorithm using time-reversal electromagnetic inversion technique[D]. Nanchang: Department of Physics, Nanchang University, 2013: 38−41.

[18] 生雪莉, 惠俊英, 梁国龙. 时间反转镜用于被动检测技术的研究[J]. 应用声学, 2005, 24(6): 351−358. SHENG Xueli, HUI Junying, LIANG Guolong. Study on passive detection technology based on an acoustic time-reversal mirror[J]. Applied Acoustics, 2005, 24(6): 351−358.

[19] 杨伏洲, 王海燕, 申晓红, 等. 基于时间反转的非均匀线阵列超指向性阵元分布模型[J]. 上海交通大学学报, 2013, 47(12): 1907−1917. YANG Fuzhou, WANG Haiyan, SHEN Xiaohong, et al. Super-direction element distribution model of NLA based on TR[J]. Journal of Shanghai Jiao Tong University, 2013, 47(12): 1907−1917.

[20] MATHEWS C P, ZOLTOWSKI M D. Eigenstructure techniques for 2-D angle estimation with uniform circular arrays[J]. IEEE Transactions on Signal Processing. 1994, 42(9): 2395−2407.

(编辑 赵俊)

Passive time reversal focusing method

LIU Wei1, FU Yongqing1, XU Da2
(1. College of Information and Communication Engineering, Harbin Engineering University, Harbin 150001, China; 2. College of Underwater Acoustic Engineering, Harbin Engineering University, Harbin 150001, China)

In order to improve the applicability for time reversal focusing method in electronic warfare, a passive time reversal focusing method based on wave equation of electromagnetic wave was proposed. Based on the time reversal invariance of wave equation in electromagnetic plane wave, a part of signals emitted from source were

and recorded by the time reversal array, and then the recorded signals were time reversed. After that, by calculating the virtually

sum signals and energy values of every observed point in the given targets area instead of the physical transmission process of time-reversed signals, are refocused at source and the observed point whose energy value of virtual

sum signals is maximal is the source point. The correctness of the proposed method was verified theoretically, and then, the simulations with the time reversal array which is a uniform circular array were performed. The results show that the passive time reversal focusing method has effectiveness and accuracy, and the proposed method has good focusing performance at low SNR.

passive time reversal; wave equation; focusing; observed points

TN911.7

A

1672−7207(2016)03−0800−07

10.11817/j.issn.1672-7207.2016.03.013

2015−03−18；

2015−06−10

国家自然科学基金资助项目(61172038) (Project(61172038) supported by the National Natural Science Foundation of China)

付永庆，教授，博士生导师，从事阵列信号处理的研究；E-mail: fuyongqing@hrbeu.edu.cn