Riordan矩阵在广义Motzkin路计数中的应用

王丽娟，杨胜良

（兰州理工大学理学院，甘肃兰州730050）

Riordan矩阵在广义Motzkin路计数中的应用

王丽娟，杨胜良

（兰州理工大学理学院，甘肃兰州730050）

用Riordan矩阵的方法研究了具有4种步型的加权格路（广义Motzkin路）的计数问题，引入了一类新的计数矩阵，即广义Motzkin矩阵.同时给出了这类矩阵的Riordan表示，也得到了广义Motzkin路的计数公式.Catalan矩阵，Schröder矩阵和Motzkin矩阵都是广义Motzkin矩阵的特殊情形.

Riordan矩阵；格路；Catalan矩阵；Schröder矩阵；Motzkin矩阵

1 引言

集合Z×Z中的点叫做xOy平面上的格点.由一些格点构成的序列P=v0v1···vn叫做长度为n的格路.格路P=v0v1···vn上的两个相邻格点vi=（ai，bi），vi+1=（ai+1，bi+1）的差vi+1-vi=（ai+1-ai，bi+1-bi）叫做一个步，i=0，1，···，n.

设C（n，k）表示所有从点（0，0）到点（n，n-k），允许步为E=（1，0），N=（0，1），并且不到直线y=x上方的格路的集合，C（n，k）为集合C（n，k）中格路的个数，即C（n，k）=|C（n，k）|.由文献［1］，C（n，k）是投票数，且

在文献［2］中，Ramírez研究了第一象限内一类具有4种步型：E=（1，0），N=（0，1），U=（1，1），V=（1，2）的加权格路的计数问题，利用这类加权格路定义了一种Riordan矩阵，这种Riordan矩阵的升对角线上的元素之和为k-Bonacci数.本文用Riordan矩阵的方法研究了具有4种步型的加权路（广义Motzkin路）的计数问题，引入了一类新的计数矩阵，即广义Motzkin矩阵.同时给出了这类矩阵的Riordan表示，也得到了广义Motzkin路的计数公式.Catalan矩阵，Schröder矩阵和Motzkin矩阵都是广义Motzkin矩阵的特殊情形.

2 Riordan矩阵

3 广义Motzkin矩阵与广义Motzkin数

这一节考虑第一象限内具有4种步型E=（1，0），N=（0，1），U=（1，1），V=（1，2）且位于对角线y=x以下的加权格路的计数问题，这些步的权分别为1，a，b，c.这样的路叫作广义Motzkin路.规定加权格路P的权w（P）是其所有步的权的乘积，加权格路P的长度l（P）是组成这条格路的步的个数.

根据上一节中Riordan矩阵的刻画，矩阵D=［D］n，k≥0为Riordan矩阵.如果取权a=0，b=c=1，则（9）式与经典的Motzkin矩阵的递推关系一样，初值也相同，所以Riordan矩阵D（1，0，1，1）就是例2.3中的Motzkin矩阵.因此称这个Riordan矩阵为广义Motzkin矩阵，称其首列元素为广义Motzkin数.

定理3.1 广义Motzkin矩阵的逆矩阵D-1的Riordan表示为：

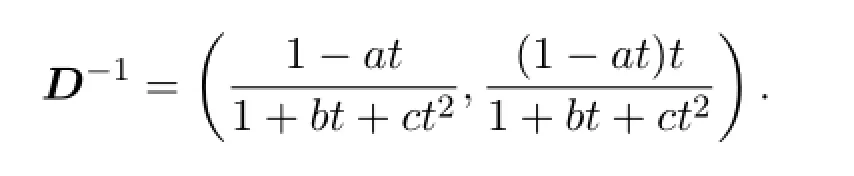
定理3.2 广义Motzkin矩阵D的Riordan表示为：

定理3.3 广义Motzkin矩阵的一般元素为：

［1］Renault M.Four Proofs of the Ballot Theorem［J］.Mathematics Magazine，2007，80（5）：345-352.

［2］Ramírez J L，Sirvent V F.A Generalization of the k-Bonacci Sequence from Riordan Arrays［J］.Electronic Journal of Combinatorics，2015，22（1）：1-20.

［3］Shapiro L W，Getu S，Woan W J，et al.The Riordan group［J］.Discrete Applied Mathematics，1991，34：229-239.

［4］Sprugnoli R.Riordan arrays and combinatorial sums［J］.Discrete Mathematics，1994，132：267-290.

［5］He Tianxiao，Sprugnoli R.Sequence characterization of Riordan arrays［J］.Discrete Mathematics，2009，309（12）：3962-3974.

［6］Merlini D，Rogers D G，Sprugnoli R，et al.On some alternative characterizations of Riordan arrays［J］. Canadian Journal of Mathmatics，1997，49（2）：301-320.

［7］Merlini D，Sprugnoli R.Algebraic aspects of some Riordan arrays related to binary words avoiding a pattern［J］.Theoretical Computer Science，2011，412（27）：2988-3001.

［8］Sprugnoli R.An Introduction to Mathematical Methods in Combinatorics［M］.Dipartimento Di Sistemi E Informatica Viale Morgagni，2006.

［9］Sloane N J A.The on-line encyclopedia of integer sequences［EB/OL］.New York：Cornell University，1964.

［10］Nkwanta A，Shapiro L W.Pell walks and Riordan matrices［J］.Fibonacci Quarterly，2005，43（2）：170-180.

The application of Riordan arrays in counting generalized Motzkin paths

Wang Lijuan，Yang Shengliang
（School of Science，Lanzhou University of Technology，Lanzhou730050，China）

By means of Riordan arrays，the counting problems of weighted latticed paths with four types of steps（generalized Motzkin paths）are studied，and a new class of enumerative arrays，i.e.，generalized Motzkin arrays，are introduced.Meanwhile，the Riordan array expressions of these arrays are given，and the counting formulas also obtained.It turns out that Catalan array，Schröder array and Motzkin array are all the special cases of the generalized Motzkin arrays.

Riordan array，latticed path，Catalan array，Schröder array，Motzkin array

O157.1

A

1008-5513（2016）02-0160-09

10.3969/j.issn.1008-5513.2016.02.007

2016-01-15.

国家自然科学基金（11561044）.

王丽娟（1988-），硕士生，研究方向：代数组合与组合优化.

2010 MSC:05A15，15A09