具有时滞离散时间捕食-食饵模型的行波解

彭华勤， 朱 庆， 肖华峰

(1.广西师范大学 数学与统计学院 广西 桂林 541006； 2.广州大学 数学与信息科学学院 广东 广州 510006)

具有时滞离散时间捕食-食饵模型的行波解

彭华勤1,2， 朱 庆2， 肖华峰2

(1.广西师范大学 数学与统计学院 广西 桂林 541006； 2.广州大学 数学与信息科学学院 广东 广州 510006)

研究了一类抽象的离散时间时滞反应扩散系统，当非线性项满足部分指数拟单调条件时行波解的存在性.利用交叉迭代方法和Schauder不动点定理，将抽象波方程行波解的存在性转化为寻找一对合适的上下解,并将所得结论应用到具有时滞离散时间的捕食-食饵模型中.

捕食-食饵模型； 行波解； 时滞； 时间离散； 上下解

0 引言

在非均匀环境下，对于许多演化过程，个体的空间分布不能忽略，因此，建立模型的时候应当考虑时间变量和空间变量.由于种群数量的变化通常是离散的，因此对某些种群建立离散时间模型更为合理.一般来说竞争合作系统的动力学行为可以通过单调动力系统的理论来研究，而对于捕食-食饵型的种群模型，单调动力系统的方法将不再适用.物种的繁殖由于受到妊娠、环境以及成熟过程等各方面因素的影响，物种密度在时间上的滞后是客观存在的.因此，具有时滞的Lotka-Volterra扩散系统受到学者们的关注[1-9].一般的两种群时滞系统可以记为

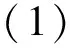
考虑到空间因素的影响，文献[5]运用单调迭代和上下解技巧讨论离散时间反应扩散方程波解的存在性

un(x)-un-1(x)=dΔun(x)+f(un(x),un-τ(x)),n∈N,x∈R,

(2)

它可以看成是连续方程

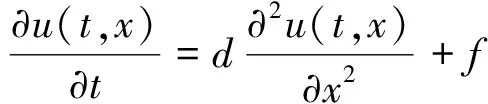
(3)

在时间格上的离散化方程.

基于上述原因，本文应用非标准有限元差分法和欧拉方法，考虑一类抽象的离散时间时滞反应扩散系统

(4)

当非线性项满足部分指数拟单调条件时行波解的存在性.

1 预备知识

定义1 系统(4)的行波解是一种特别形式的平移不变的解,它的具体表达形式为

un(x)=φ(x+cn)，vn(x)=ψ(x+cn)，

其中：φ,ψ∈C2(R,R);c>0是一个常数，称为传播速度.

将un(x)=φ(x+cn)，vn(x)=ψ(x+cn)代入到式(4),并且记φs(t)=φ(t+s)，ψs(t)=ψ(t+s)，以及将x+cn以t代替，可得

(5)

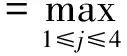
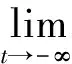
(6)其中(φ-,ψ-)和(φ+,ψ+)是式(5)的两个平衡点.不失一般性，假设φ-=0,ψ-=0,φ+=k1>0,ψ+=k2>0，则式(6)变为

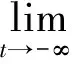
(7)

根据式(7),假设

(P1) 存在k=(k1,k2)，满足ki>0，使得fi(0,0)=fi(k1,k2)=0，i=1,2.

(P2) 存在两个正常数L1，L2，使得

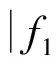
为方便起见，记

C[0,M](R,R2)={(φ,ψ)∈C(R,R2):0≤φ(s)≤M1,0≤ψ(s)≤M2,s∈R}.

定义算子H= (H1,H2):C[0,M](R,R2)→C(R,R2)为:

H1(φ,ψ)(t)=f1(φt(-cτ1),ψt(-cτ2))+(β1-1)φ(t)+φ(t-c),

H2(φ,ψ)(t)=f2(φt(-cτ3),ψt(-cτ4))+(β2-1)ψ(t)+ψ(t-c).

根据H1和H2的形式，系统(5)可以改写为

(8)

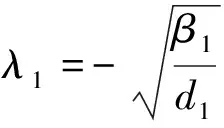
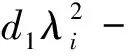
对任意(φ,ψ)∈C[0,M](R,R2)，定义F=(F1,F2):C[0,M](R,R2)→C(R,R2)为:

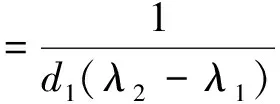
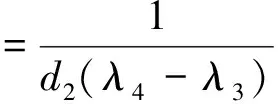
易知F=(F1,F2)有意义，并且对任意(φ,ψ)∈C[0,M](R,R2)，F1(φ,ψ)(t)，F2(φ,ψ)(t)，满足

因此，如果F(φ,ψ)=(F1(φ,ψ),F2(φ,ψ))=(φ,ψ),(φ,ψ)是F的一个不动点，则系统(5)有一个解(φ,ψ)，如果这个解进一步满足渐近边界条件(7)，则它是式(4)的一个行波解.

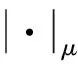
2 系统(6)的行波解的存在性

系统(4)中当非线性项满足部分指数拟单调条件(简称为(PQM*))时行波解的存在性.首先介绍部分指数拟单调条件的概念为:

(PQM*) 存在两个正常数β1和β2,使得

f1(φ1(-cτ1),ψ1(-cτ2))-f1(φ2(-cτ1),ψ1(-cτ2))+(β1-1)[φ1(0)-ψ1(0)]≥0,

f1(φ1(-cτ1),ψ1(-cτ2))-f1(φ1(-cτ1),ψ2(-cτ2))≤0,

f2(φ1(-cτ3),ψ1(-cτ4))-f2(φ2(-cτ3),ψ2(-cτ4))+(β2-1)[ψ1(0)-ψ2(0)]≥0,

其中φ1,φ2,ψ1,ψ2∈C([-cτ,0],R)满足

1) 0≤φ2(s)≤φ1(s)≤M1,0≤ψ2(s)≤ψ1(s)≤M2，s∈[-cτ,0].

2) eβ1s[φ1(s)-φ2(s)]，eβ2s[ψ1(s)-ψ2(s)]关于s∈[-cτ,0]是非降的.

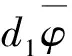
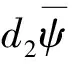
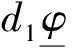
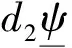
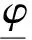
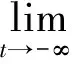
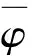
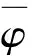
引理1 假设(PQM*)成立，则

H1(φ2,ψ1)(t)≤H1(φ1,ψ1)(t),

H1(φ1,ψ1)(t)≤H1(φ1,ψ2)(t),

H2(φ2,ψ2)(t)≤H2(φ1,ψ1)(t),

其中:t∈R,φi,ψi∈C(R,R),i=1,2，满足

0≤φ2(s)≤φ1(s)≤M1;

0≤ψ2(s)≤ψ1(s)≤M2，s∈R.

引理1的结论由(PQM*)的定义可以直接计算得到.

引理2 假设(PQM*)成立,则对任意(0,0)≤(φ,ψ)≤(M1,M2)，有

F1(φ2,ψ1)(t)≤F1(φ1,ψ1)(t)，

F1(φ1,ψ1)(t)≤F1(φ1,ψ2)(t)，

F2(φ2,ψ2)(t)≤F2(φ1,ψ1)(t)，

其中：t∈R，φi,ψi∈C(R,R)，i=1,2;0≤φ2(s)≤φ1(s)≤M1,0≤ψ2(s)≤ψ1(s)≤M2,s∈R.

定义轮廓集为

引理4 假如(P1)和(PQM*)成立，则FΓ⊂Γ.

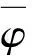
引理3～5以及定理1的证明与文献[6]中的证明类似, 在此省略.

3 应用

利用第2部分的结果来证明具有时滞的离散时间捕食-食饵系统

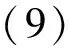
行波解的存在性，其中un(x),vn(x)分别表示两种群在时刻n、位置x处的密度.

假设c>0，令

un(x)=φ(x+cn)=φ(t)，vn(x)=ψ(x+cn)=ψ(t)，t=x+cn，

则对应的波方程为

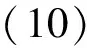
系统(10)满足渐近边界条件

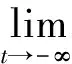
(11)

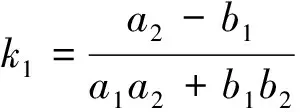
定义f(φ,ψ)=(f1(φ,ψ),f2(φ,ψ))为

f1(φ,ψ)=r1φ(0)[1-a1φ(-cτ1)-b1ψ(-cτ2)],

f2(φ,ψ)=r2ψ(0)[1+b2φ(-cτ2)-a2ψ(-cτ4)],

易得f1,f2满足假设(P1)和(P2)，现在证明f(φ,ψ)=(f1(φ,ψ),f2(φ,ψ))满足(PQM*).

引理6 当τ1>0，τ4>0，且都充分小时，函数f(φ,ψ)满足(PQM*).

为了应用定理1，构造适当的上下解.

定义Δ1c(λ)=d1λ2+e-λc+r1-1,Δ2c(λ)=d2λ2+e-λc+r2(1+b2/a1)-1,则可以得到引理7.

引理7 假设00，使得当c>c*时，Δ1c(λ)和Δ2c(λ)分别有两个正实根λ1,λ2和λ3,λ4满足λ1<λ2，λ3<λ4，进一步得到

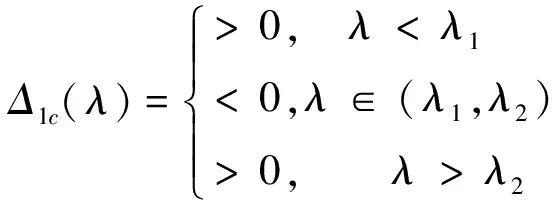
令η∈(1,min{2,λ2/λ1,λ4/λ3,(λ1+λ3)/λ1,(λ1+λ3)/λ3})，对于充分大的q>0，定义两个函数

l1(t)=eλ1t-qeηλ1t，l2(t)=eλ3t-qeηλ3t，

易知l1(t)，l2(t)均有一个全局最大值，分别记为c1,c2>0，则存在

使得eλ1t1-qeηλ1t1=c1,eλ3t3-qeηλ3t3=c2.对任意给定的λ>0,存在ε2>0，ε4>0,使得k1-ε2e-λt1=c1，k2-ε4e-λt3=c2. 由于a2>b1，进一步假设a1k1>b1k2成立，使得这个正平衡点对应于常微分系统是稳定的平衡点，则存在ε0>0，ε1>0，ε3>0，使得

a1ε1-b1ε4>ε0;a2ε3-b2ε1>ε0;a1ε2-b1ε3>ε0;a2ε4-b2ε2>ε0.

(12)

定义下面的连续函数:

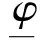
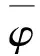
以及

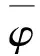
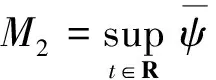
min{t2,t4}-cmax{1,τ1,τ2}≥max{t1,t3}.

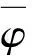
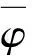
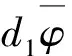
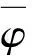
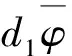
当t2≤t≤t2+cτ1，得到

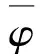
注意到k1+ε1e-λt2=eλ1t2，从而

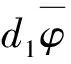
由于τ1充分小，所以存在ε*(0<ε*<ε0/[a1(k1+ε1)])使得1-ε*ε0，得到

L1(0)≤r1(k1+ε1)[a1k1-a1(1-ε*)(k1+ε1)+b1ε4]<0，

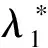
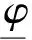
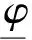
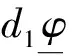
当t≤t1，有

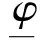
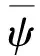
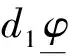
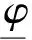
定理2 如果00，τ4>0，且都充分小时，系统(12)有连接平衡点(0,0)和(k1,k2)的行波解(φ(x+cn),ψ(x+cn))，且满足

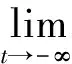
[1] DUNBAR S R.Traveling wave solutions of diffusive Lotka-Volterra equations [J].Journal of mathematical biology，1983，17(1)：11-32.

[2] HONG K，WENG P X.Stability and traveling waves of a stage-structured predator-prey model with holling type-II functional response and harvesting[J].Nonlinear Anal RWA，2013，14(1)：83-103.

[3] ZHANG G B，LI W T，LIN G.Traveling waves in delayed predator-prey systems with nonlocal diffusion and stage structure[J].Mathematical and computer modelling，2009，49(5/6)：1021-1029.

[4] ZHANG X，XU R.Global stability and travelling waves of a predator-prey model with diffusion and nonlocal maturation delay[J].Communications in nonlinear science and numerical simulation，2010，15(11)：3390-3401.

[5] 李秋英.具有时滞和不育控制的捕食模型的Hopf分支[J].郑州大学学报(理学版)，2016，48(4)：23-26.

[6] 郝丽杰，蒋贵荣，鹿鹏.具有垂直传染的SIRS传染病模型分岔分析[J].郑州大学学报(理学版)，2013，45(2)：31-36.

[7] Roeger L I W.Dynamically consistent discrete Lotka-Volterra competition models derived from nonstandard finite-difference schemes[J].Discrete and continuous dynamical systems，2008，2(2)：415-429.

[8] LIN G，LI W T.Traveling wave fronts in temporally discrete reaction-diffusion equations with delay[J].Nonlinear analysis real world applications，2008，9(1)：197-205.

[9] XIA J，YU Z.Traveling wave solutions in temporally discrete reaction-diffusion systems with delays[J].Zamm-journal of applied mathematics and mechanics，2011，91(10)：809-823.

(责任编辑：方惠敏)

Traveling Wave Solutions in Temporally Discrete Delayed Prey-predator Model

PENG Huaqin1,2， ZHU Qing2， XIAO Huafeng2

(1.SchoolofMathematicsandStatistics,GuangxiNormalUniversity,Guilin541006,China; 2.SchoolofMathematicsandInformationScience，GuangzhouUniversity，Guangzhou510006，China)

The existence of traveling wave solutions for general discrete time reaction diffusive system with delay when the nonlinear term satisfies the partial exponential quasi monotone condition was investigated.By using the cross iteration method and Schauder′s fixed point theorem，the existence of traveling wave solutions was reduced to search a pair of upper and lower solutions.Finally，a discrete time delay prey-predator type model with spatial diffusion was considered to illustrate the results.

prey-predator model； traveling wave solution； delay； temporally time； upper-lower solution

2016-09-05

国家自然科学基金项目(11371107，11301102)；广州市属高校科研项目(1201431215).

彭华勤(1984—)，男，江西抚州人，博士研究生，主要从事生物数学研究，E-mail：huaqinpeng@126.com.

O175.2

A

1671-6841(2017)02-0037-06

10.13705/j.issn.1671-6841.2016219