异构多导弹系统自适应分布式协同制导
毛昱天, 杨 明,张 锐
(中国兵器工业导航与控制技术研究所, 北京 100089)
异构多导弹系统自适应分布式协同制导
毛昱天, 杨 明,张 锐
(中国兵器工业导航与控制技术研究所, 北京 100089)
针对异构多导弹系统的分布式协同制导问题,在传统比例导引律的基础上设计出一类领航跟随分布式协同制导律。运用代数图论、分布式网络同步原理以及非线性系统一致性理论, 领弹采用基于固定系数的比例导引律,从弹采用基于可变系数的参数自适应比例导引律。该领航-跟随分布式自适应协同制导律可使领弹和从弹实现对目标的同时攻击,且各相邻导弹间仅传输各自的可测状态信息,算法具有较低的通信代价和较好的可扩展性。最后给出了相关数值仿真算例,仿真结果验证了控制算法的有效性。
多导弹系统;协同制导;自适应比例导引;分布式一致性
0 引言
随着反导技术的快速发展,综合一体化的现代防御体系正逐步形成, 单枚导弹突破防御和高效毁伤目标将变得愈发困难,未来战争系统将演变为系统与系统、体系与体系间的对抗。多枚导弹通过信息交互与共享实现功能互补,可有效提高系统综合作战效能和突防能力,如增强战术隐身和电子对抗能力,增强对目标的饱和攻击能力等[1-3],完成单枚导弹很难完成的任务,更加符合未来作战发展的趋势,同时现代信息化、网络化技术的不断发展也为多弹协同攻击的实现创造了条件。
协同制导律作为多弹协同作战的关键技术之一,是实现对目标精确打击的前提。目前,关于多导弹系统分布式协同制导律分析与设计的研究比较有限。文献[1]和文献[2]讨论了多导弹协同制导律的约束条件和各类导引律的方法和特点。文献[3]将攻击时间可控制导律与一致性分散化协调算法相结合,设计了一类多导弹编队齐射攻击的分散化协调制导律, 该算法需要对剩余飞行时间进行预估。文献[4]提出了一种攻击时间可控制导律,并将其应用于反舰导弹的编队齐射攻击,该制导律需预先人工指定攻击时间来实现协同攻击,但不能实现导弹之间的自动协同。文献[5]在共享导弹之间剩余飞行时间和飞行距离的基础上进一步设计了寻的导弹的协同制导律。文献[6]提出了一种基于领弹和被领弹策略的多导弹时间协同制导律,领弹采用经典比例导引律,从弹制导指令采用时标分离和动态逆控制方法,该方法要求所有被领弹与领弹之间必须进行通信。文献[7]运用非线性系统跟踪控制原理,提出了一种基于虚拟领弹且时间可控的多导弹协同制导方法。文献[8] 在构造多枚导弹综合代价函数的基础上,研究了多枚导弹共同拦截机动目标的协同制导律设计问题,但该综合代价函数应用时受到约束较多,且在攻击之前各单枚导弹需获知参与攻击导弹数目等全局信息。上述基于领弹或虚拟领弹的协同制导方法均要求所有各从弹与领弹之间必须进行通信或各从弹均需获知整个多导弹系统的全局信息, 本质上是一种集中式控制结构,鲁棒性和可扩展性较差,也不利于导弹实现战术隐身与静默攻击。
本文基于代数图论、分布式网络同步原理和多智能体系统受控一致性理论,提出一种基于邻接个体局部信息交互的领弹-从弹异构多导弹系统分布式自适应协同制导方法,可实现所有导弹对于给定目标的同时攻击,与集中式控制方式相比,具有通信量小、动态重构性和可扩展性好等优点。
1 多导弹协同制导模型
假设所有导弹具有相同的通信能力,其通信半径均为R,各导弹的通信邻域用半径为R的虚线圆圈表示。不失一般性,考虑由1枚领弹和n枚从弹组成的多导弹系统,对领弹和各从弹进行自然编号,即领弹编号为0,各从弹编号依次为1~n。图1给出了基于局部通信拓扑结构的4枚导弹系统的分布式协同制导模型原理图,领弹M0和各从弹Mi(i=1,2,3) 间采用最近邻通信方式,即各导弹仅与在其通信邻域范围内的相邻导弹进行信息交互,特别地,与领弹具有直接通信连接关系的从弹才能受到领弹的直接牵引。

图1 多导弹系统协同制导模型Fig.1 Cooperative guidance model of multi-missile systems
图2给出了领弹M0和各从弹Mi与目标的相对运动关系。其中,r0、ri为领弹M0和从弹Mi与目标的相对距离;v0、vi为领弹M0和从弹Mi的飞行速度;q0、qi为领弹M0和从弹Mi与目标的弹目视线角;σ0、σi为领弹M0和从弹Mi的速度矢量角;η0、ηi为领弹M0和从弹Mi的速度矢量前置角。

图2 领弹M0和从弹Mi与目标的相对运动关系Fig.2 Relative motion between M0 and Mi
假设目标静止不动,可得领弹M0和从弹Mi相对目标的导引关系方程如下:
(1)
其中,a0和ai为领弹M0和从弹Mi的法向加速度指令,进而设计如下经典比例导引律:
(2)
其中,N0为领弹M0比例导引系数,取为常值;Ni为从弹Mi的比例导引系数,设计为可变的自适应调节参数。综合式(1)和式(2),可得M0和Mi在比例导引下的闭环制导模型:
(3)
进一步假设M0和Mi均采用“比例导引+分布式协同导引”的制导策略,据此可以得到M0和Mi的协同制导律如下:
(4)
其中,g01、g02和gi1、gi2分别为叠加在M0和Mi的比例导引基础上的协同导引控制分量,用于各邻接导弹间的信息交互以在线调整各自的速度和方位。
对于多弹协同攻击而言,若在攻击目标后期能够保证ri=r0、ηi=η0,或者ri=r0、ηi=-η0,则领弹M0与所有从弹Mi将实现同时抵达目标[6], 具体如图3所示。

(a) 情形1(a) Senario 1

(b) 情形2(b) Senario 2图3 领弹M0和从弹Mi飞行末段运动示意图Fig.3 Motion of terminal guidance between M0 and Mi
2 异构多导弹系统协同制导律
2.1 分布式自适应协同制导律设计
不失一般性,考虑系统中存在一个领弹的情形,基于如图1所示的分布式异构多导弹协同网络的通信拓扑结构,给出各导弹分布式协同导引结构原理图,具体如图4所示。

图4 多导弹系统分布式协同制导原理图Fig.4 Scheme of distributed cooperative guidance of multi-missile systems
参考图4的分布式协同架构,整个系统的通信拓扑分为两部分:从弹与从弹间的通信拓扑,领弹与从弹间的通信拓扑,具体模型见文献[9]。
根据式(4),定义多导弹系统状态向量x=[r,η]T,进而得到M0和Mi,i=0,1,2,...,n的状态向量如下
(5)
进一步可得
(6)
定义M0和Mi的分布式协同控制分量为
g0=[g01,g02]T
gi=[gi1,gi2]T,i=1,2,…,n
(7)
结合式(4)、式(6)和式(7),可得领弹-从弹分布式闭环协同制导模型
(8)
其中,x0和xi分别为M0和Mi的制导状态向量;f(·)为非线性制导系统模型;g0和gi分别为M0和Mi的分布式协同制导分量。多导弹系统协同制导律设计本质上为在模型(8)的基础上,设计分布式协同制导分量及参数自适应调节规律,使领弹与从弹状态趋于一致,实现对于目标的同时攻击。为此,将分布式自适应协同制导律设计分为两部分:分布式协同制导策略和比例导引参数自适应调节机制。
首先,基于分布式动态网络一致性原理[13],为M0和Mi选择分布式系统制导分量如下:
(9)
其中,Δ0和Δi分别代表领弹和从弹的通信邻域,由于通信连接关系的对称性,有μji=μij,αji=αij。此时Mi的闭环制导模型变为
γ0iβ0i(x0-xi)
(10)

δ0iβ0i(ηi-η0)]
φ0iβ0i(ηi-η0)]
(11)
同理可得从弹Mi闭环制导模型具体形式为

(12)
进一步,为从弹Mi设计比例导引系数自适应调节律
(13)
其中,Pi为正定对称常数矩阵,ωi(xi,t)满足
f(xi,Ni,t)=f(xi,N0,t)+ω(xi,t)(Ni-N0)
(14)
其中,f(xi,N0,t)=[-vicos(ηi),(1-N0)visin(ηi)/ri]T,将式(6)代入式(14),可得
(15)
将式(15)代入式(13),可得
φijαji(ηj-ηi)]
(16)
2.2 分布式协同制导收敛性分析
设多导弹系统对应的通信拓扑为G,G的关联矩阵和拉普拉斯矩阵分别为D和L[11-12],定义Lf为所有从弹所形成的加权拉普拉斯矩阵(WeightedLaplacian),定义对称矩阵[13-14]
LKΛ=D(IμijIΛij)DT
(17)
其中,Iμij和IΛij分别定义为对角处为μij和Λij的分块对角矩阵。定义(μΛ)ijs为μijΛij的对称部分。根据异构多智能体分布式网络受控一致性收敛原理,若领航-跟随多导弹系统通信网络满足连通性,且运动模型为f(·),Lf和L满足下述条件[14-15]
(18)
则所有从弹Mi状态与领弹M0状态渐近趋同,即
(19)
式(18)中λi(·),i=1,…,n代表矩阵特征值,且各特征值满足λ1(·)≤λ2(·)≤…≤λn(·),λmax(·)代表矩阵的最大特征值,m为系统状态向量维数。式(18)即为领航跟随多导弹分布式协同制导系统实现状态渐近收敛的充分条件,直接反映了可实现非线性异构多导弹系统受控状态一致性对于系统运动模型和通信拓扑模型的具体要求。
3 数值仿真
如图4所示,考虑由1枚领弹M0和3枚从弹Mi,i=1,2,3共4枚导弹所组成的异构多导弹网络通信拓扑结构,其中领弹M0仅与从弹M1进行通信交互,之间采用局部邻接通信方式。假定被攻击目标为固定目标,导弹初始速度为 vi=300m/s,i=0,1,2,3,速度矢量在xoy平面变化规律为:
v0x(t)=300cos(σ0(t)),
v0y(t)=300cos(σ0(t))
(20)
vix(t)=300cos(σi(t))
viy(t)=300cos(σi(t)),i=1,2,3。
其中,速度方向角为σ0、σi,i=1,2,3的变化规律依照式(1)、式(2)、式(11)和式(12)进行调节。
进一步,领弹选取固定比例导引系数N0=3,各从弹比例导引系数按照式(12)和式(13) 进行自适应在线参数调节,初值Ni(0)=3,i=1,2,3,权矩阵选择为数Pi=1,i=1,2,3。仿真步长为 0.1s,进一步为满足分布式协同制导收敛条件,选择通信耦合加权矩阵为:
(21)
为实现对目标的协同攻击,要求各导弹同时到达目标点。多导弹系统对应的通信拓扑结构如图1所示。目标初始位置坐标为(30000m, 9500m)。各导弹的初始位置、初始速度和初始前置角如表1所示。
图5给出了系统的飞行轨迹曲线图,*代表目标点,其他彩色曲线为各导弹的运动轨迹。图6给出了各导弹对运动目标的跟踪误差随时间的变化曲线,可以看出,领弹和各从弹对于目标的距离跟踪误差同时收敛,代表其可实现对于目标的同时攻击。图7给出了各导弹的速度方位角随时间的变化规律,可见所有导弹速度方位最终可实现渐近趋同。图8给出了各导弹协同制导指令随时间的变化规律。

表1 各导弹初始参数Tab.1 The initial parameters of all missiles
图9给出了各从弹的比例导引系数变化规律,可以看出,各从弹的比例导引系数调节过程主要在飞行初始阶段,随后很快实现收敛,中后期阶段的协同控制主要依靠速度的大小和范围的分布式协调来实现。
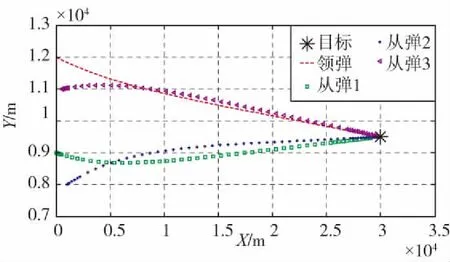
图5 协同导引下各导弹飞行轨迹Fig.5 Trajectories of all missiles with cooperative guidance law

图6 协同导引控制下各导弹跟踪误差Fig.6 Tracking errors of all missile with cooperative guidance law

图7 协同导引控制下各导弹速度方位角Fig.7 Orientations of all missiles with cooperative guidance law

图8 各导弹协同制导指令Fig.8 Guidance laws of all missiles

图9 协同导引控制下各从弹比例导引系数Fig.9 Proportional guidance coefficients of all follower missiles
进一步,分别将各导弹在纯比例导引(无协同控制律)、固定系数比例导引(Ni=3,i=0,1,2,3)以及分布式自适应比例导引下的飞行时间进行对比,具体结果如表2所示。在纯比例导引律作用下,无法实现各导弹对于给定目标的同时攻击,前后到达时间差最大可达到约8s,而在分布式自适应协同比例导引律作用下,不仅可以实现同时协同攻击,且弹目相对距离协同收敛速度快于固定系数的比例导引律,这是由于各导弹从速度大小和方向、比例导引系数等各方面分别进行了分布式自适应协同的结果。

表2 各导弹飞行时间Tab.2 The flight time of all missiles
综合上述仿真结果, 基于最近邻通信交互机制下的分布式协同制导控制律, 可以实现领航跟随异构多导弹系统的分布式协同制导和对于目标的同时攻击,有效地验证了分布式自适应协同制导控制算法的有效性和优越性。
4 结论
本文研究了具有领弹-从弹通信拓扑结构的多导弹系统协同攻击目标的分布式自适应制导律设计问题,将经典比例导引律、自适应变参数比例导引律与非线性分布式一致性控制律有机结合,提出了完全分布化的异构多导弹分布式自适应协同制导律设计方法,实现了领弹和从弹对于目标的同时攻击,且无需估计导弹剩余飞行时间。该制导律仅需相邻导弹之间传输各自的可测状态信息,具有典型的局部通信和分布式计算的特点, 且制导律形式简单、通信量少,便于工程实现,能够在提高导弹攻击突防概率的同时降低对从弹弹载计算机和探测设备要求, 从而有效降低成本。
[1] 王建青,李帆,赵建辉,等.多导弹协同制导律综述[J].飞行力学,2011, 29(4): 6-10.
[2] 张克, 刘永才, 关世义.体系作战条件下飞航导弹突防与协同攻击问题研究[J].战术导弹技术, 2005, 10(2): 1-7.
[3] 邹丽,周锐,赵世钰,等.多导弹编队齐射攻击分散化协同制导方法[J].航空学报, 2011, 32(2): 281-290.
[4] Jeon I S, Lee J I, Tahk M J.Impact-time-control guidance law for anti-ship missiles[J].IEEE Transactions on Control Systems Technology, 2006, 14(2): 260-266.
[5] 赵世钰, 周锐.基于协调变量的多导弹协同制导[J].航空学报, 2008, 30(6): 1605-1611.
[6] 张友安, 马国欣, 王兴平.多导弹时间协同制导:一种领弹-被领弹策略[J].航空学报, 2009, 30(6): 1109-1118.
[7] Zhao S Y, Zhou R.Cooperative guidance for multi-missile salvo attack[J].Chinese Journal of Aeronautics, 2008, 21 (6):533-539.
[8] Shaferman V, Shima T.Cooperative optimal guidance laws for imposing a relative intercept angle[C].AIAA Guidance, Navigation, and Control Conference, 2012:12-18.
[9] 毛昱天,杨明,张锐,等.领航跟随多导弹系统分布式协同制导[J].导航定位与授时,2016,3(2):20-24.
[10] Zhao S Y, Zhou R, Chen W.Design of time-constrained guidance laws via virtual leader approach[J].Chinese Journal of Aeronautics, 2010, 23(1): 103-108.
[11] Godsil C, Royle G.Algebraic graph theory[M].New York: Springer Verlag, 2001.
[12] Horn R A, Johnson C R.Matrix analysis[M].London: Cambridge University Press, 1985.
[13] Wang W, Jean E S.Adaptive synchronization in coupled dynamic networks[J].New York: Cornell University Library, 2004,10(2):245-250.
[14] Wang W, Jean E S.A theoretical study of different leader roles network[J].IEEE Transactions on Control Systems Technology, 2006, 51(7): 1156-1161.
[15] Slotine J E, Wang W.A study of synchronization and group cooperation using partial contraction theory[C].Block Island Workshop on Cooperative Control , 2004:1-9.
Distributed Adaptive Cooperative Guidance for Heterogeneous Multi-missile Systems
MAO Yu-tian, YANG Ming, ZHANG Rui
(Chinese Ordnance Navigation and Control Technology Research Institute, Beijing 100089, China)
To solve the problem of decentralized cooperative guidance of heterogeneous multiple missiles, a set of distributed leader-follower cooperative guidance law is developed based on the traditional proportional guidance law. On the basis of the algebraic graph theory, the principles of synchronization in distributed networks and the consensus theory of nonlinear systems, the distributive cooperative guidance law of the leader missile is based on the proportional guidance law with fixed navigation coefficient, while the distributive cooperative guidance law of each follower missile is based on the proportional guidance law with adaptive variable navigation coefficient. The synchronized attack on the target could be achieved via the proposed leader-follower cooperative guidance law, which relies on only local interaction with measurable states and exhibits low communication cost as well as good scalability. Finally, nontrivial numerical simulations are performed to verify the effectiveness of the proposed control algorithm.
Multi-missile systems; Cooperative guidance; Adaptive proportional guidance; Distributed consensus
10.19306/j.cnki.2095-8110.2017.03.007
2016-11-15;
2017-02-01
毛昱天(1984-),男,博士,助理研究员,主要从事制导武器系统总体及控制方面的研究。E-mail: yutianmao@163.com
U666.12
A
2095-8110(2017)03-0039-07

