具有收缩因子的自适应鸽群算法用于函数优化问题
郭瑞+赵汝鑫+吴海舟+任东+范佳伟


摘 要:文中在鸽群算法的基础上添加收敛因子并使用自适应策略,通过标准的函数优化对算法进行了测试,实验结果表明,通过添加收敛因子和自适应策略的鸽群算法能有效提高收敛速度且具有一定竞争力,同时验证了在一些情况下全局搜索的优越性。
关键词:鸽群算法;收敛因子;自适应策略;测试函数;群智能优化算法
中图分类号:TP114 文献标识码:A 文章编号:2095-1302(2017)05-00-04
0 引 言
元启发式优化技术非常流行,在过去二十年,它们中的一些算法如遗传算法,蚁群算法和粒子群算法在计算机科学领域及其他科学领域非常有名[1]。基于群体的群体智能算法已被广泛接受,并成功应用于求解优化问题中。近年来,出现许多基于群体的群体智能算法,如人工蜂群算法[2],人工鱼群算法[3]和布谷鸟算法[4]等。一些生物启发优化算法正在尝试模拟自然生态系统机制,增强现代优化技术的可行性,为复杂组合優化问题提供了切实可行的解决方案。对基于生态机制创建的元启发式算法进行改进,使算法具有更好的收敛速度,并提高原算法的竞争力。
1 鸽群算法及收缩因子与自适应策略
鸽群算法(Pigeon-Inspired Optimization,PIO)[5]是一种群智能优化算法,该算法的灵感来源于鸽群利用地磁和地标归巢,对归巢过程分析建立的数学模型。一项检测鸽子在不同磁场探测能力的调查表明:鸽子具有很强的归巢能力,是因为鸽子嘴上的铁晶体可以根据地磁场强弱为鸽子指明方向。在古罗马时代就有人知道鸽子具有归巢的本能,而信鸽在较早时就被用作通信工具。当信鸽距离自己目的地较远时利用地磁场来辨别方向,当距离目的地较近时就利用当地地标进行导航。信鸽利用地磁场和地标可以很容易地找到目的地。在PIO中地图和指针算子模型的提出基于地磁场和太阳,而地标算子模型的提出则基于地标。收缩因子和策略的添加能使PIO算法具有更快的收敛速度和优越性。
1.1 地图模型
地图模型的建立基于地磁场,我们分别用xi和yi来表示第i只鸽子的位置和速度。在二维空间里,位置和速度在每次迭代中进行更新。第i只鸽子的速度和位置将用如下公式进行迭代计算:
(1)
(2)
第i只鸽子的速度由它上一代速度和当前鸽子最好位置和所在位置共同决定,其中R是地图因子,rand是一个随机数,t为代数。而第i只鸽子的位置由之前的位置和当前速度决定。所有鸽子的飞行均通过地图来保证,进行比较可得到鸽子的最好位置,即Xg。每一只鸽子将根据公式(1)向拥有最好位置的鸽子进行方向调整和飞行,而公式(2)则进行的是位置调整。
1.2 地标模型
地标模型根据鸽子利用地标来进行导航而建立。在利用地标导航时,距离目的地的位置比利用地图导航的距离更近,如果鸽子对现在所处位置地标不熟悉,则在附近鸽子的带领下飞行,当找到标志性建筑物或者熟悉位置时,则根据经验自由飞行。在地标模型中,用Np来记录每一代中一半鸽子的个数,Xc(t)为第t代所有鸽子的中心位置,假如每一只鸽子可以飞直线距离到达目的地,将有如下公式:
(3)
(4)
(5)
公式中,fitness(x)是每只鸽子的质量,当fitness(Xi (t))= 1/[fmin(Xi (t))+ε]时,针对的是最小优化问题;当fitness(Xi(t))= fmax(Xi(t))时,则针对的是最大优化问题。用Xp来代替每次迭代的最优位置,Xp=min(Xi1,Xi2,...,XiNc)。所有鸽子的中心是每次迭代的目的地,在Np之外的鸽子将跟着那些靠近目的地的鸽子飞行。而靠近目的地的鸽子将更快地飞到目的地。
1.3 添加收缩因子及自适应策略
鸽群优化算法的基本思想来源于对鸽群归巢过程的研究及行为模拟。在原始PIO算法基础上提出一种改进的收缩因子PIO(Constriction Factor PIO,CFPIO)算法,用以加速算法收敛。CFPIO算法在收敛性方面效果良好。速度更新原则如下:
(6)
其中,,φ=φ1+φ2,φ>4。添加收缩因子后发现CFPIO容易陷入局部最优,因为鸽群不断向全局最优靠拢,当鸽群的位置接近全局最优位置Xg,速度更新公式的第二项为0时,鸽子位置就得不到更新,出现停滞情况。若出现这种情况,便重新初始化鸽群的i位置,以增强鸽群活力,避免因停滞而陷入局部最优。
在CFPIO的基础上添加一个位置因子γ(γ≥0),测试鸽子当前位置与全局最优鸽子的距离d(d=‖X-G‖2),速度因子ε(ε≥0),判断鸽子的飞行速度,一旦鸽子接近Xg(d<γ),并且飞行速度小于设定的速度因子ε(|V|<ε),则认为该鸽子可能出现停滞,对该鸽子进行位置初始化,保持鸽子的多样性,增加活力,以避免局部最优。
2 结果与讨论
2.1 实验环境与参数设置
本文使用10个基准测试函数来验证添加收缩因子的鸽群算法的有效性和可行性。本实验采用Matlab R2012a编写仿真程序,在Windows XP、主频为2.99 GHz,RAM为1.75 GB的PC机上实现。除添加收缩因子的鸽群算法(CFPIO)外,实验中还用到蝙蝠算法(BA)以及PIO。设置种群数量为20个,最大迭代次数为1 000次,维数为20,采用独立运行30次最优的平均值作为测试结果。
2.2 测试函数
由于单峰函数和多峰函数各有所长,所以在该仿真实验中,主要选取这两类基准测试函数,函数f1~f5是单峰,函数f6~f10是多峰。两类函数的区别在于多峰函数有大量局部最优值,它们对探测检查和避免局部最优有好处。而单峰函数只有全局最优值,这适合标记算法的开采。实验中用到的10个测试函数如下:
(1)Step函数
,-100≤xi≤100(i=1,2,…,n;n=30),在(0,0,…,0)处取得全局最小值0。
(2)Rosenbrock函数
,-30≤xi≤30(i=1,2,…,n; n=30),在(0,0,…,0)处取得全局最小值0。
(3)Schwefels 2.22 函数
,-10≤xi≤10(i=1,2,…,n;n=30),在(0,0,…,0)处取得全局最小值0。
(4) Schwefels 1.2 函数
,-100≤xi≤100(i=1,2,…,n;n=30),在(0,0,…,0)处取得全局最小值0。
(5)Sphere函数
,-100≤xi≤100(i=1,2,…, n; n=30),在(0,0,…,0)处取得全局最小值0。
(6)Penalized2函数
,-50≤xi≤50(i=1,2,…,n; n=30),在(0,0,…,0)处取得全局最小值0。
(7)Penalized1函数
其中,-50≤xi≤50(i=1,2,…,n; n=30),在(0,0,…,0)处取得全局最小值0。
(8)Griewangk函数
,-600≤xi≤ 600(i=1,2,…,n;n=30),在(0,0,…,0)处取得全局最小值0。
(9)Ackley函数
,-32≤xi≤32(i=1,2,…,n; n=30),在(0,0,…,0)处取得全局最小值0。
(10)Rastrigin函数
,-5.12≤xi≤5.12(i=1,2,…,n; n=30),在(0,0,…,0)处取得全局最小值0。
2.3 实验结果
实验结果见表1所列。
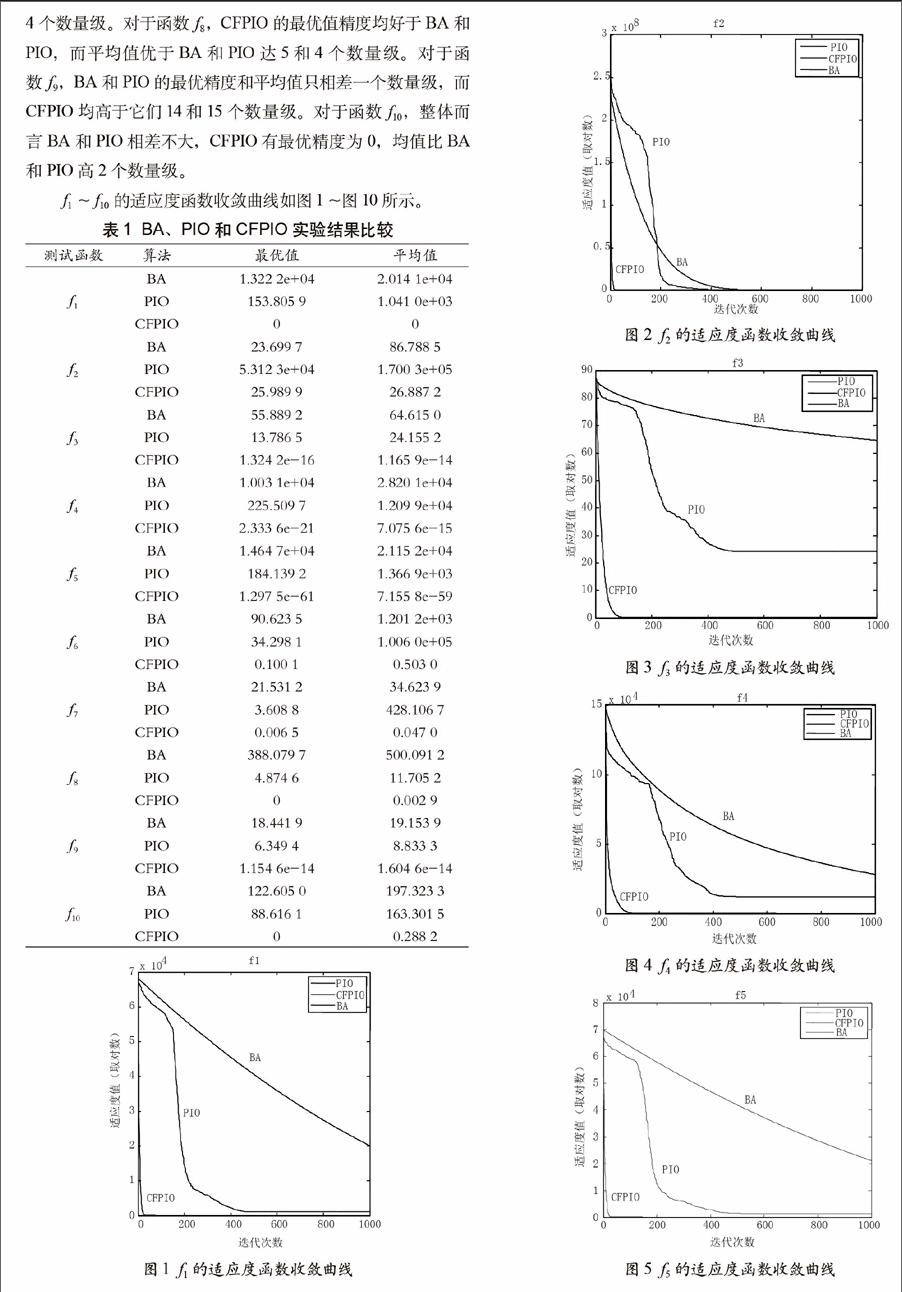
从表1可看出,在单峰函数方面,对于函数f1,CFPIO的最优精度和平均值可达到0,均比PIO和BA高。对于函数f2,BA的最优精度相对于CFPIO较好,均比PIO高出2个数量级,在平均值方面CFPIO和BA都比PIO高3个数量级。对于函数f3,CFPIO的最优值精度和平均值都比BA和PIO高14个数量级。对于函数f4,BA与PIO在最优精度和平均值方面相差不大,而CFPIO在最优精度和平均值方面比它们高出25个和19个精度。对于函数f5,PIO比BA的最优精度和平均值分别高出1个数量级,而CFPIO比PIO高出62个数量级。
在多峰函数方面,对于函数f6,CFPIO的最优值精度比BA和PIO高3个数量级,而平均值分别高4和6个数量级。对于函数f7,CFPIO的最优值精度达到e-3,分别比BA和PIO高4和5个数量级,而平均值分别比BA和PIO高出3和4个数量级。对于函数f8,CFPIO的最优值精度均好于BA和PIO,而平均值优于BA和PIO达5和4个数量级。对于函数f9,BA和PIO的最优精度和平均值只相差一个数量级,而CFPIO均高于它们14和15个数量级。对于函数f10,整体而言BA和PIO相差不大,CFPIO有最优精度为0,均值比BA和PIO高2个数量级。
f1~f10的适应度函数收敛曲线如图1~图10所示。
表1 BA、PIO和CFPIO实验结果比较
测试函数 算法 最优值 平均值
f1 BA 1.322 2e+04 2.014 1e+04
PIO 153.805 9 1.041 0e+03
CFPIO 0 0
f2 BA 23.699 7 86.788 5
PIO 5.312 3e+04 1.700 3e+05
CFPIO 25.989 9 26.887 2
f3 BA 55.889 2 64.615 0
PIO 13.786 5 24.155 2
CFPIO 1.324 2e-16 1.165 9e-14
f4 BA 1.003 1e+04 2.820 1e+04
PIO 225.509 7 1.209 9e+04
CFPIO 2.333 6e-21 7.075 6e-15
f5 BA 1.464 7e+04 2.115 2e+04
PIO 184.139 2 1.366 9e+03
CFPIO 1.297 5e-61 7.155 8e-59
f6 BA 90.623 5 1.201 2e+03
PIO 34.298 1 1.006 0e+05
CFPIO 0.100 1 0.503 0
f7 BA 21.531 2 34.623 9
PIO 3.608 8 428.106 7
CFPIO 0.006 5 0.047 0
f8 BA 388.079 7 500.091 2
PIO 4.874 6 11.705 2
CFPIO 0 0.002 9
f9 BA 18.441 9 19.153 9
PIO 6.349 4 8.833 3
CFPIO 1.154 6e-14 1.604 6e-14
f10 BA 122.605 0 197.323 3
PIO 88.616 1 163.301 5
CFPIO 0 0.288 2
圖1 f1的适应度函数收敛曲线
图2 f2的适应度函数收敛曲线
图3 f3的适应度函数收敛曲线
图4 f4的适应度函数收敛曲线
图5 f5的适应度函数收敛曲线
图6 f6的适应度函数收敛曲线
图7 f7的适应度函数收敛曲线
图8 f8的适应度函数收敛曲线
图9 f9的适应度函数收敛曲线
图10 f10的适应度函数收敛曲线
由上图可知,当迭代结束时,CFPIO优于BA和PIO。CFPIO不仅收敛速度快,且其算法收敛精度接近0。通过以上各函数的优化结果可以看出,该改进算法有效、可行。
3 结 语
对PIO算法添加收缩因子和自适应策略进行分析,该算法模拟了鸽群归巢的特性,利用地磁场和地标向目的地飞行。从函数优化结果可以看出,收缩因子和自适应改善了鸽群算法,不仅可有效提高收敛速度,还让鸽群算法具有竞争力,也验证了在一些情况下全局搜索的优越性。此外,虽然添加收缩因子和策略后的PIO提高了收敛速度,但在求解一些复杂收敛速度问题时速度较慢,收敛精度偏低,稳定性较差,而这些问题将在后期进行进一步研究。
参考文献
[1] Seyedali Mirjalili, Seyed Mohammad Mirjalili, Andrew Lewis. Grey Wolf Optimizer[J].Advances in Engineering Software, 2014,69(3):46 - 61.
[2] Karaboga D, Basturk B.A powerful and efficient algorithm for numerical function optimization: artificial bee colony algorithm[J]. Journal of Global Optimization2007,39(3): 459-471.
[3] LI X L,SHAO Z,QIAN J .An optimizing method based on autonomous animats: fish-swarm algorithm[J].Systems Engineering Theory and Practice,2002,22(11) : 32-38.
[4] Rajabioun R.Cuckoo optimization algorithm[J].Applied Soft Computing,2011,11(8):5508-5518.
[5] Haibin Duan ,Peixin Qiao.Pigeon-inspired optimization:a new swarm intelligence optimizer for air robot path planning[J]. International Journal of Intelligent Computing and Cybernetics,2014, 7(1):24-37.
[6]錢伟懿,王艳杰.带自适应压缩因子粒子群优化算法[J].辽宁工程技术大学学报,2010,29(5):949-952.
[7]胡欣欣.求解函数优化问题的改进布谷鸟搜索算法[J].计算机工程与技术,2013,34(10):3639-3642.
[8]聂建亮,程传录,郭春喜,等.基于粒子群优化算法的多因子自适应滤波[J].武汉大学学报(信息科学版),2013,38(2):136-139.

