一道高考试题的解法分析与命制背景——2016年天津市高考数学理科第20题

浙江省宁波市镇海区龙赛中学 (315200) 梅 洁

一道高考试题的解法分析与命制背景
——2016年天津市高考数学理科第20题

浙江省宁波市镇海区龙赛中学 (315200) 梅 洁

1 试题呈现

已知函数f(x)=(x-1)3-ax-b，x∈R，其中a,b∈R.

(Ⅰ)求f(x)的单调区间；

(Ⅱ)若f(x)存在极值点x0，且f(x1)=f(x0)，其中x1≠x0，求证x1+2x0=3；

2 试题简评

本试题表述严谨，朴实无华，解法灵活.题目3个小问，呈现平和自然，问题与问题之间相互联系，层层递进，易于激发学生解决问题的兴趣.作为一道压轴题，以三次函数为背景,主要考查导数在研究函数性质(单调性、极值、最值)与证明不等式中的应用，充分考查学生推理论证能力和数形结合、分类讨论、转化与化归等数学思想.第Ⅰ问属于学生较熟悉的题型，考查导数与函数单调性的关系、考查分类讨论的数学思想.第Ⅱ问考查导数与函数极值之间的关系以及考查三次方程的根与系数之间的关系.第Ⅲ小题是一个证明题，解决三次函数的最大值的最小化问题，此问题的实质是函数的逼近问题，是第一类切比雪夫多项式的一种特殊情况，该问题是近几年高考、联赛中的热门问题，其背景深厚，内涵丰富，要求具有较强的运算能力，灵活的转化与化归思想.总体上，试题设计立意鲜明，角度宽，视点多，充分体现了“以能力立意为指导，考查能力和素质”的命题原则.

3 试题解析

3.1 第(Ⅰ)小题的分析与解答

第Ⅰ问求原函数的单调区间，可转化为导函数的零点分布问题，可采用分类讨论，也可采用参数分离，这2种方法是解决函数单调性问题的通性通法.本题采用分类讨论来处理较为妥当.

评注：由于方程f′(x)=0是否有解与a的正负性有关，因此在解答中对a的正负性作为分界点讨论.分类讨论是导数压轴题中常见的数学思想，处理该类问题首先要理清为何要讨论，其次确定讨论标准，要求做到不重不漏，这些都是分类讨论的关键.

3.2 第(Ⅱ)小题的分析与解答

第(Ⅱ)小题证明一个恒等式，实质是证明三次方程根与实数的关系，处理该类问题一般可以从三个角度去考虑：1、函数角度，2、方程角度，3、作差比较.学生只需要一定的运算能力和分析能力，能够较快地分析出解题的思路，从而有较好的入手点

评注：先验证f(3-2x0)=f(x0)，再说明f(x)=f(x0)的根有且只有两个不同的根，从而得到x1=3-2x0，使问题得到顺利解决.

解法2:(方程角度)令f(x1)=f(x0)=c，则x0,x1是方程f(x)-c=0的两个不等实根；又因为x0是f(x)的极值点，所以x0即是g(x)=f(x)-c的零点也是极值点；所以x0是方程f(x)-c=0的二重根.又因为f(x)-c=0，即x3-3x2+(3-a)x-1-b-c=0;由三次函数的韦达定理知x0+x0+x1=3，即2x0+x1=3得证.

评注：先分析x0是方程g(x)=0的二重根，x1是方程g(x)=0的一重根；从而就很容易想到2x0+x1为三根之和，故采用韦达定理易证.

解法3:(做差比较)因为f(x1)=f(x0)，则f(x1)-f(x0)=0，代入函数表达式，得(x1-x0)[(x1-1)2+(x0-1)2+(x0-1)(x1-1)-a]=0(1);又由解法1知a=3(x0-1)2，则等式(1)可化简为(x1-x0)2[2x0+x1-3]=0；又因为x1≠x0，所以2x0+x1=3.

评注：因为f(x)为多项式函数，且函数值f(x1)=f(x0)，采用作差比较，通过代数恒等变形，转化为自变量之间的恒等关系也是一种比较常用的方法，考查代数恒等变形的能力及转化与化归的数学思想.

3.3 第(Ⅲ)小题的分析与解答

第(Ⅲ)小题证明一个含绝对值的多元不等式，实质上是一个函数逼近问题，是第一类切比雪夫多项式n=3时的情况，具有深厚的高等数学背景，解决这类问题常采用的方法：1、分类讨论，2、赋值法，3、数形结合.本问题的解决需要学生较高的综合分析能力，较强的代数运算能力，能巧妙利用对称思想的能力.

解法1:(分类讨论)设g(x)在区间[0,2]上的最大值为M，max{x,y}表示x,y两数中的最大值.根据f(x)在[0,2]上单调性的不同情况分三种情况进行分类讨论：

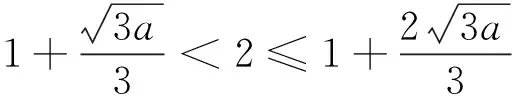
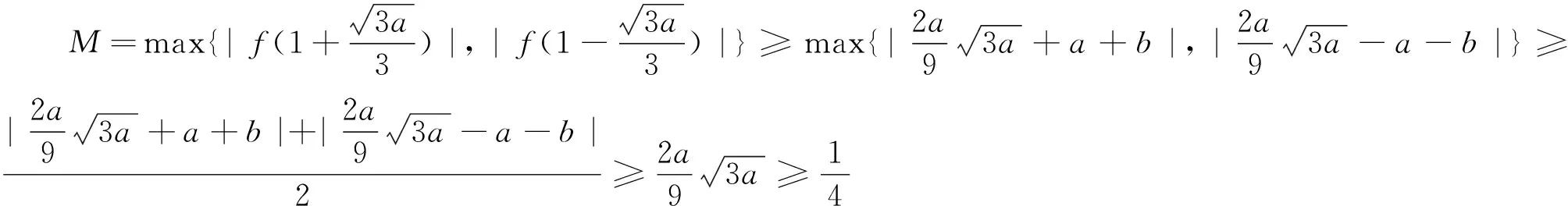
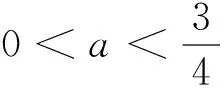
评注：求f(x)在区间[0,2]上的最大值，先考虑函数在区间[0,2]上的单调性与a是否大于3有关，因此在解答中对a=3作为分界点讨论.再通过比较端点函数值与极值之间的大小关系进行讨论.

解法2:(赋值法)设g(x)在区间[0,2]上的最大值为M，max{x,y}表示x,y两数中的最大值.

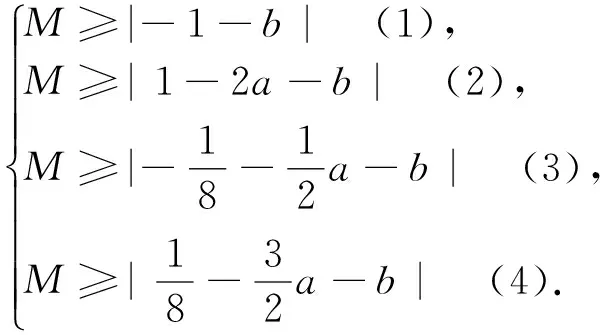
由(1)和(2)知

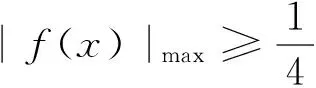
更一般性的结论：

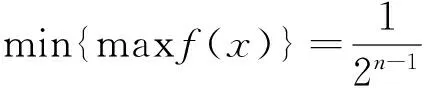
这可能是这个问题的出题背景吧.

下面再从几何角度来看看这个问题

几何解释:原问题等价于在区间[0,2]上，存在a>0，b∈R，使得g(x)≤M恒成立，求M的最小值. 因为|(x-1)3-ax-b|≤M，即ax+b-M≤(x-1)3≤ax+b+M.原问题又可以转化为在区间[0,2]上，存在a>0，b∈R,y=(x-1)3的图像“夹在”两条平行直线l1:y=ax+b-M与l2:y=ax+b+M之间.求l1,l2两条直线纵截距之差的绝对值的最小值.

图1

4 教学启示

教师在日常的教学中在保证基础知识，基本技能落实好的前提下加强各种数学思想方法的渗透，如数形结合、分类讨论，转化化归等思想，同时还要在平时教学中渗透高等数学中的思想、观点、方法，加大初等知识和高等知识交叉点的研究与学习，优化知识结构.只有学生学会了思考和研究的方法，掌握了基本的数学思想，能像数学家一样去思考问题，成绩水平才能真正提高.

同时教师还应在平时加强高考试题研究，由于高考命题具有连续性，因此加强高考试题的研究，有助于把握高考试题的发展方向，尤其是研究高考中最能体现题目本质特征的解法，理解试题的命制背景和特点，才能发挥它在高中数学教学中的导向作用.本题的背景在前几年的各省高考试题及数学联赛中多次出现，比如2009年湖北高考理科数学第21题，2010年全国数学联赛第9题，2015年1月浙江省学业水平考试第34题.如果在平时教学中，能够引导学生思考数学问题背后的内容，往往可以捕捉到高考命题的一丝线索.

[1]沈虎跃.一道竞赛试题的解法分析与命题背景[J].中学教研(数学)，2009(10)：34-36.

[2]佩捷，林常.切比雪夫逼近问题[M].哈尔滨工业大学出版社，2013:1-10.

[3]杨瑞强.青山不言自用翠——2016年全国课标Ⅰ卷理科第21题[J].中学教研(数学)，2016(10):35-37.