高中数学中的关系、映射与反演方法浅说

王剑

在医院，我们常常会看到外科医生在诊断内伤病人时，先请病人透视拍片，再根据底片判断内伤的位置和程度，从而制订治疗方案，然后，按照这一方案进行治疗.外科医生的这种工作方法，我们在处理数学问题时也常常用到，例如，

解方程6x2-2x+6+x2-2x=21.

很显然本题直接求解难度较大，于是令y=x2-2x+6，可把原方程转化为y2+6y-27=0，从而求得y=3或y=-9（舍），进而得到x2-2x+6=3，所以，原方程的解为x1=-1，x2=3.

上面的例子给出了如下数学方法的生活背景和简单举例.

一、关系、映射、反演方法的阐释

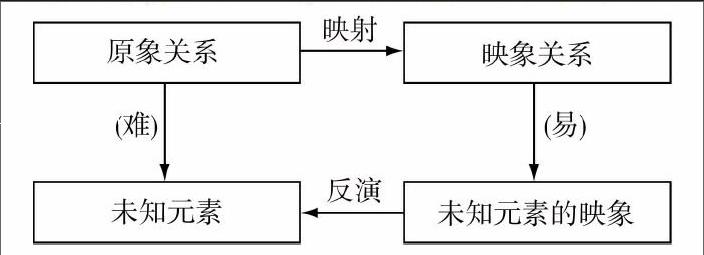
一个数学问题，都是由一些已知的数学对象、数学关系和待定的数学对象与关系（都称为“原象”）组成的，我们希望由此求得未知的元素，如果直接求解比较困难时，往往可以寻求一个映射，把“原象”映射成“映象”，通过映象关系求得未知元素的映象，最后，“反演”求得未知元素.

RMI是关系（Relationship）、映射（Mapping）、反演（Inversion）的简称，这一过程可以用如下框图表示：

RMI方法是一种普遍的工作方法，它可以化生为熟、化难为易、化繁为简，在高中数学中有着广泛的运用，例如，换元法，对数法，复数法与向量法，坐标法，參数法，数学模型法等，都可以被理解为RMI方法的应用.

二、RMI方法在高中数学中的应用

（一）换元法

本文开头举的例子本质上就是通过换元法求解的，可见，换元法是RMI方法的典型应用.

例1若p∈R且|p|<2，不等式（log2x）2+plog2x+1>2log2x+p恒成立，求实数x的取值范围.

分析如果把不等式看成关于log2x的不等式，则问题很难入手，于是我们通过变换主元，看成关于p的一次不等式，则容易解决.为了化超越不等式为代数不等式，我们可以令a=log2x，于是不等式可以写成（a-1）p+a2-2a+1>0，再将其转化为函数，令f（p）=（a-1）p+a2-2a+1，根据题意f（p）>0恒成立，即

f（2）>0，

f（-2）>0 2（a-1）+a2-2a+1>0，

-2（a-1）+a2-2a+1>0，

解得a>3或a<-1，对应x>8或0

通过换元法可以将一些元素化归，化超越不等式为代数不等式，化无理不等式为有理不等式，化高次不等式为低次不等式等，在运用RMI方法时，关键就在于选取恰当的映射，使问题中本难解决的元素变得易于确定.

（二）复数法与向量法

一个复数z=x+iy本质上是由一对有序实数（x，y）唯一确定的，于是能够将平面上的点与全体复数建立一一对应的关系.在高中数学中，向量的概念是作为复数的一个几何意义提出来的，这样一来，以原点为起点的向量与复数、复平面上的点这三者间建立了一个映射关系，彼此可以互相转化.

例2诱导公式cosπ12-α=sinα，sinπ12-α=cosα的复数证明.

证明令z=cos（-α）+isin（-α），则

iz=cosπ12+isinπ12[cos（-α）+isin（-α）]

=cosπ12-α+isinπ12-α，

又iz=icos（-α）+i2sin（-α）=sinα+icosα，

由复数相等的条件可以推得cosπ12-α=sinα，

sinπ12-α=cosα.

例3若等边三角形ABC的边长为23，平面内一点M满足CM=116CB+213CA，则MA·MB=.

分析本题可以选取不共线的CB和CA作为一组基底，其他向量可用这一基底线性表示.

答案-2（过程略）.

解决向量问题的途径之一就是寻找一组合适的基底，然后，将题中所有向量通过映象关系用基底线性表示，最后，反演得到结论，使问题得以很好解决.这也是“基本量”在RMI方法中的经典例证.

当然本题也可建立适当的坐标系，把几何问题映射为代数问题，通过代数运算求出未知关系，把该关系通过反演解决某个几何问题，在高中阶段，坐标法通常是指平面直角坐标系和极坐标系.

（三）参数法

参数法，顾名思义，就是在解决某一数学问题时，根据问题的特点，合理地选择其长度、面积、角度、体积等参数，由其映象关系简化运算、降低难度.对于平面解析几何的问题，可运用其参数方程，也是参量法解题的一个重要方面，体现了RMI方法对于高中数学中的解析几何问题的优越性.

例4（2016年高考全国Ⅰ卷第20题）设圆x2+y2+2x-15=0的圆心为A，直线l过点B（1，0）且与x轴不重合，l交圆A于C，D两点，过B作AC的平行线交AD于点E.

（Ⅰ）证明|EA|+|EB|为定值，并写出点E的轨迹方程；

（Ⅱ）设点E的轨迹为曲线C1，直线l交C1于M，N两点，过B且与l垂直的直线与圆交于P，Q两点，求四边形MPNQ面积的取值范围.

解（Ⅰ）所求轨迹方程为x214+y213=1（过程略）.

（Ⅱ）根据题意，直线l过点B（1，0）且与x轴不重合，所以直线l的倾斜角不为π12.

可设直线MN的参数方程为x=1+tcosθ，

y=tsinθ （t为参数，θ为倾斜角）.①

因为直线PQ与直线MN垂直，所以倾斜角相差π12，

所以直线PQ参数方程为x=1-msinθ，

y=mcosθ （m为参数，θ+π12为倾斜角）.②

将 ① 代入x214+y213=1，

整理得（3+sin2θ）t2+6tcosθ-9=0（Δ>0）；

∴t1+t2=-6cosθ13+sin2θ，t1t2=-913+sin2θ，

∴|t1-t2|=（t1+t2）2-4t1t2

=36cos2θ+36（3+sin2θ）13+sin2θ=1213+sin2θ.

同理将②代入圆方程x2+y2+2x-15=0中，

整理得m2-4msinθ-12=0（Δ>0）；

∴m1+m2=4sinθ，m1m2=-12，

∴|m1-m2|=（m1+m2）2-4m1m2=43+sin2θ，

∴S=112|t1-t2|·|m1-m2|=24113+sin2θ，0<θ<π，

∴S∈[12，83）.

分析本题考查的是椭圆的标准方程和直线的相关知识，对运算能力要求较高，一般来说，对于直线和圆锥曲线的交点问题，常常是联立方程组通过韦达定理来求解的，这种常规思路的求解一来计算量较大，二来学生容易产生思维定式，不利于学生创新思维的培养.笔者采用参数方程的方法，不仅开拓了解题思路，且能提高学生观察、分析问题的能力.

三、RMI方法在高中数学教学中的意义

自从数学家徐利治先生完善了RMI方法后，该方法就成为数学学习与研究的基本方法之一，尤其是利用RMI方法指导解题时，往往能够化生为熟，化难为易，化繁为简，达到事半功倍的效果.RMI方法有利于锻炼学生的数学思维，培养学生的数学核心素养.

（一）锻炼学生的数学思维

数学学习是一个学生自己经历发现、理解和反思数学问题的过程，数学问题多来源于生活，所以在学习过程中学生多把数学知识与已有生活经验联系起来，而数学概念高度抽象的特点，又让学生产生困惑，这种“联系”与“困惑”是RMI方法产生的原因.《普通高中数学课程标准（实验稿）》倡导在教师的引导下，让学生经历“数学化”和“再创造”的活动过程.这个过程最初是由数学教育学家弗赖登塔尔提出来的，他认为：“数学研究的对象，是现实世界同一类事物或现象抽象而成的量化模式.”

RMI方法作为问题解决的策略性方法越来越受到一线教师和教育专家的重视，他们认为使用RMI方法解题时，能够更好地关注学生的解题思路，锻炼学生的数学思维.

（二）培养学生的数学核心素养

教育部《普通高中数学课程标准》修订组组长王尚志教授提出，中国学生在数学学习上应当培养好数学抽象、直观想象、数学运算、逻辑推理、数学建模、数据分析六大核心素养.

《标准》也鼓励学生进行数学探究活动，强调“在数学过程中应该让学生充分地经历探索事物的数量关系，变化规律的过程”.换句话说，学生的“学”已经从接受学习变为探究发现学习，更加注重学习过程与学习体验，更加讲究学习策略和学习方法，在这样的背景之下，RMI方法作为一种问题解决策略，强调发现未知元素与已有经验间的联系，从而可以建立适当映射，通过处理映象关系反演得到最终结果，这与新课程中“注重数学问题（概念、原理、法则、公式）的发生、探索、发现、论证及应用的全过程展开”和“重视培养学生的自主学习和探究能力”这两方面不谋而合.

通过RMI方法，可以引导学生发现零碎知识点间的联系，从而将这些知识系统化，并纳入自己的知识体系之中，指导他们像数学家一样，面对新的问题时，通过探索和学习，发现事物变化的起因和内在联系，从而真正理解学习，达到培养学生核心素养的目的.

当然，在我们充分肯定RMI方法在高中数学教与学中的重要作用的同时，也应注意到，RMI方法也是不断更新的，不能一味地使用旧的模式和思路，并且在原象与映象之间的有效映射也受每个人的认知结构和数学能力的制约，所以要不断学习，分析和认识高中数学各知识之间的联系，不断将数学知识系统化.

本文探讨了RMI方法的释义及其在高中数学中的应用与意义，不当之处，还望同仁批评指正.

【参考文献】

[1]郑毓信.数学教育视角下的“核心素养”[J].数学教育学报，2016（03）：1-5.

[2]朱立明.基于深化课程改革的数学核心素养体系构建[J].中国教育学刊，2016（05）：76-80.

[3]滕吉红，黄晓英.高等数学中的RMI原則应用实例[J].高师理科学刊，2015（05）：64-66.

[4]马云鹏.关于数学核心素养的几个问题[J].课程·教材·教法，2015（09）：36-39.

[5]张建桥.高考“苏派风格”观照下学生数学核心素养探微[A].江苏省教育学会.2015江苏省教育学会学术年会报告文集[C].江苏省教育学会，2015：7.

[6]谭珺文，谢静兰.例说RMI原则在高中函数、方程、不等式中的应用——以2014年高考数学题为例[J].广西教育，2014（34）：119-121，128.