HPM视角下的高中数学教学优化设计例析

陈天宇

[摘 要] 数学史以其丰富的数学思想方法、深刻的数学文化内涵，成为创造学生数学学习动机的重要载体. 文章基于学生数学学习的认知发展过程，结合高中数学的学科特点及课程理念，从HPM的视角对高中数学教学设计做出优化和改进方案，论述了数学史无可比拟的教育价值.

[关键词] 数学史；数学教学；教学设计

数学是推动科技发展的关键学科之一，也是伴随人类社会发展生生不息的一门学科. 评价如此之高的数学学科，学生怎会对其缺乏兴趣，而丧失学习动机呢？HPM研究很好地回答了这一问题.

[?] HPM研究的意义和价值

毋庸置疑，数学教学的最终目的是促进学生对数学知识的理解和运用，教学设计也必须基于这一目标进行. 尽管各个教学环节的设计经过精心打磨，从情境引入，到复习旧知，到活动探究，最后到归纳总结，都看似很“完美”，且衔接过渡顺畅，其中不乏教师的些许创意. 但大多数情况下，学生学习数学的主动性很难被调动起来，只是被动地接受一些概念、性质、定理、公式、解法等具体的数学知识，却无暇顾及对“为什么要学”、“学到的内容有什么用”等问题的思考，消退和遗忘成为时间推移的必然结果.

HPM（History and Pedagogy of Mathematics），含义为“数学史在数学教学中的渗透”，自1972年第二届国际数学教育大会上第一个HPM国际研究小组成立以来，一直备受广大数学教育工作者的关注. HPM研究主要涉及数学教育取向的数学史研究、基于数学史的教学设计、历史相似性研究、数学史融入数学教学的行动研究四个方面.

数学教育除了数学技术的教学，还应该有人文精神的传承.重结果，轻过程的数学教育是走不远的，随着学习的深入，学生只会更加讨厌数学. 数学史恰好提供了这样一个平台，从历史的角度重新审视数学知识，关注数学知识的发生和形成过程，对学习数学知识的必要性给予了强有力的回答，丰富教师的课堂教学，激发学生的学习兴趣，预见学生的认知发展，促进学生的数学理解培养学生的人文气息. 既然数学教育的目的是培养学生终身发展所需的6个核心素养，那么数学史就是维持学生终身学习数学的精神支柱[1].

[?] HPM视角下的教学设计优化案例

1. 历史发生原理的启示

虚数的概念在高中数学体系中无疑是一大亮点，将数系从实数域扩张到了复数域. 可能是因为复数在高考中的地位无足轻重，无非是一道选择题或填空题，广大教师们在引入虚数概念时，搬用教材上的x2+1=0在实数域上无解的例子，从而定义i=，i为虚数单位. 如此展开教学显然是不合适的，要知道数学家们花了三百多年才理解复数，我们的学生在寥寥几语中就能明白虚数为何物了吗？我们不妨追溯一下数学家探索虚数的历程.

后来，笛卡尔在他的著作《几何学》中对负数开平方后得到的数起名为“imaginary figure”，意为“虚无缥缈的数”，虚数单位i正是来源于此.

由此可见，17世纪一流的头脑在面对虚数时都会如此困惑不解，我们的学生在短短几分钟内就能超越古人理解虚数了吗？显然，用x2+1=0引入虚数是失败的. 学生对数学问题的理解过程和数学在历史上的发展过程具有相似性，此即为历史发生原理.正如M·克莱因所说：“历史上数学家们所遇到的困难，也正是学生的学习障碍”. 因此，借助卡尔达诺和莱布尼兹的例子作为引入更能激起学生认知结构的冲突，前者让学生初步感知虚数的存在，后者让学生感受虚数和实数之间存在某种联系，从而为学生创造学习动机.

2. 在历史中寻找数学认知起点

如果要深入数学史与数学教育的关系层面，就必须考虑知识的发生过程，教师除了教授新的知识点，还要寻找学生的认知起点，把新知识建立在学生已有认知基础之上.

导数的几何意义是刻画函数单调性的重要工具，也是沟通初等数学与高等数学的桥梁. 学生在瞬时变化率概念和极限思想Δx→0的引导下，理解了导数的定义. 在引入导数的几何意义时，常用的方法是运用极限的思想，将曲线上两点的割线的斜率转化为曲线在其中某一点处切线的斜率. 该方法实质上是从导数的定义式入手，联系直线的斜率公式k=，再将两点无限逼近，从割线过渡到切线. 其不足之处也是显而易见的，其一，忽视了研究曲线的切线的数学背景，学生不能认识到为何要通过割线来引入切线；其二，没有对曲线的切线做明确定义，学生容易将其和其他概念相混淆，缺乏严谨性. 带着这两个问题，我们不妨去数学史中寻找改进措施.[3]

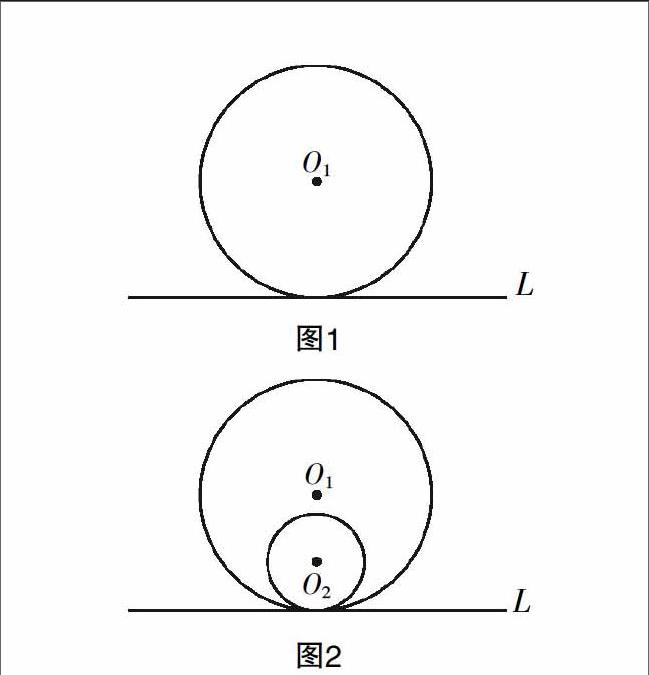
切线问题被数学家誉为17世纪最有用的数学问题，为此我们不妨先了解一下切线的历史，这样才能让学生知道我们为何要引入切线. 历史上切线研究的必要性源于三大问题：①光学问题.光在平面上的反射规律，人们早已耳熟能详，入射角=反射角，那么曲面上光的反射规律如何探究，入射角和反射角该如何确定？这就需要找出入射点处的切线位置.②运动问题. 做曲线运动的质点在某一时刻的运动方向如何确定？没有切线角？更为一般的，一条曲线和一条直线存在夹角吗？寸步难行. ③曲线夹角问题. 两条相交的曲线是否存在夹角？图1所示，过圆上一点作圆的切线，圆和直线之间有夹角吗？假设夹角不存在，可以在切点处构造一个半径较小的圆与直线相切，如图2所示. 如此一来，直观感觉上切点附近弧与直线间的空间增加了. 但反之，如果夹角存在，欧几里得却又令我们很失望，他在《几何原本》中给出命题：“过圆上一点有且仅有一条切线.” 换言之，圆和切线之间插入的第二条直线必然和圆相交于两点，如此说来，角是不存在的. 古希腊数学家们在没有微积分的情况下对此是束手无策的. 所以在17世纪，来自光学、力学、几何学三大领域的问题令数学家们感受到研究更为一般的曲线的切线的必要性.

教师可以从圆出发，让学生回顾圆的切线的定义. 圆的切线主要有3种定义方式，分别为：①与圆只有一个公共点的直线，②过圆上一点且垂直于该点与圆心连线的直线，③到圆心的距离等于圆的半径的直线. 接着，让学生反思，上述定义是否适用于圆锥曲线呢？显然不适用，以抛物线为例，对称轴与抛物线只有一个焦点，但不是切线. 学生很自然会对定义添加约束条件，得到“与曲线只有一个公共点且不穿过曲线的直线”. 这就是古希腊数学家给出的适用于圆锥曲线的切线定义，但是适用于更为一般的曲线吗？反之，如圖3所示的直线与三角函数y=sinx的图像有不止一个交点，它是曲线的切线吗？如此展开教学的目的在于启发学生重新审视自己的数学认知，激发学习动机.