基于非参数和半参数CARR模型的上海股票市场波动性研究

郭名媛，韩志楠

(天津大学 管理与经济学部， 天津 300072)

基于非参数和半参数CARR模型的上海股票市场波动性研究

郭名媛，韩志楠

(天津大学 管理与经济学部， 天津 300072)

以上证综指日对数价格的极差为研究对象，分别建立参数、半参数和非参数CARR(1,1)模型来研究上海股票市场的波动性。采用MSE、MAE两种误差度量指标比较参数、非参数、半参数CARR(1,1)模型的拟合能力。结果表明：半参数CARR(1,1)模型在对上海股市波动性的拟合方面表现最优，非参数CARR(1,1)模型次之，GCARR(1,1)模型最差。

局部线性估计；非参数CARR模型；半参数CARR模型；波动性；拟合能力

Abstract: Previous empirical results reveal that CARR significantly outperforms GARCH in the prediction of volatility. As we all know, the estimation of CARR is based on the function form and the residual’s distribution. It is because the estimation of the nonparametric and semi-paremetric CARR ignores the hypothesis, and the two models can reduce the error obviously. By using the daily range data of Shanghai composite index, we establish the parametric, nonparametric and semi-paremetric CARR to study Shanghai stock market’s volatility. We select MSE and MAE to compare the fitting ability of the three models. The results show that among the three models, the best one to feature shanghai stock market’s volatility is semi-parametric CARR, and the nonparametric CARR is inferior and the weak one is parametric CARR.

Keywords: local linear method; nonparametric CARR; semi-parametric CARR; volatility; fitting

ability

1 研究背景

近年来，证券市场中金融工具的价格波动逐渐引起投资者的关注，同时也成为了学术界的研究热点。有关金融工具价格波动性的模型被相继提出。例如，Engle[1]提出了自回归条件异方差模型(auto-regression conditional heteroscedasticity， ARCH)。基于ARCH模型，Bollerslev[2]提出了广义ARCH模型(generalized auto-regression conditional heteroscedasticity， GARCH)。随后GARCH模型的理论内容不断完善，并且产生了许多衍生模型，如指数GARCH、求和GARCH，最终形成了GARCH类模型。随着GARCH类模型理论的丰富，该类模型被大量运用于实证研究中。

GARCH类模型是基于采用收盘价格计算的收益率序列构造的。Parkinson[3]提出使用极差预测股价波动性比使用收盘价更有效；Chou[4]在2005年提出了条件自回归极差模型(conditional auto-regressive range， CARR)，该模型借鉴GARCH模型的建模思想，刻画了极差的动态结构。自从CARR模型被提出以来，该模型与GARCH模型的对比成为了研究的热点。Heng-Chih Chou[5]选取金融时报100指数和日经225指数为样本数据进行实证研究，比较了CARR模型和GARCH模型的预测能力，结果表明CARR模型在波动率估计和预测方面比GARCH模型表现更好，结果还显示在英国市场和日本股票市场中都存在着杠杆效应。国内学者程细玉等[6]也在这方面做了很多研究，通过选取美元对港币的5 min汇率比价和美元对日元的15 min汇率比价研究CARR类和GARCH类模型的性质，结果都表明CARR类模型比相同形式的GARCH模型在价格波动预测方面有更好的效果。张苏林[7]以我国黄金现货市场的主要交易品种Au99.95为研究对象，建立GARCH模型和CARR模型来研究其波动率，结果表明CARR模型在波动率预测面优于GARCH模型。此外，有学者在CARR模型中引入外生变量来研究引入的变量是否对模型的预测能力有影响。比如，耿立艳等[8]将最小二乘支持向量回归机(LSSVR)应用于CARRX模型，通过对沪深300指数的预测实证分析，发现在长期预测中，基于LSSVR估计的CARRX模型能捕捉到极差波动率的变动趋势。卢米雪[9]以混合分布假说理论为分析框架，选取了2010年1月4日至2013年4月26日沪深300指5 min数据位研究对象，运用CARR-X模型对我国股市的交易量与价格波动之间的动态关系进行了实证研究，结果表明交易量对股价波动有部分解释作用，且解释能力主要来自非预期的交易量部分。除此之外，基于CARR模型的风险价值研究也受到了学者的青睐，Ray Chou等[10]、Heng-Chih Chou等[11]以及国内学者赵树然等[12]等都在这方面做了大量研究。

以上学者所做的研究都是基于参数CARR模型。参数CARR模型是极差的条件期望与残差项的乘积，而极差的条件期望则为极差的条件期望的滞后期与极差的滞后期的函数，其中残差项的分布需人为假设。当参数估计出来后，极差的条件期望的函数形式就十分明确，还可利用估计出的参数对模型进行解释。但是参数CARR模型的估计结果依赖于极差的条件期望的函数形式和对残差项的分布所做的假设，采用不同形式的模型或者假设残差项服从不同的分布就可能得出不同的结论。为了避免参数CARR模型依赖于模型形式这一缺陷，有必要建立非参数和半参数CARR模型。

非参数模型由于完全不依赖设定的模型形式，所以能削减因模型设定错误而带来的误差。非参数模型的一般形式为：

Yi=m(Xi)+εi,i=1,2,…,n

(1)

其中：m为未知回归函数。如何估计该模型中的未知函数，很多学者都做了大量研究。Wand等[13]介绍了使用核估计方法来进行未知函数的估计；Fan[14]、Fan等[15]提出了局部多项式的估计方法；Green等[16]、Stone[17]都采用了样条估计的方法对一般非参数模型中的未知函数形式进行了拟合。Bühlmann等[18]给一般非参数模型中的变量赋予了实际意义，提出了基于非参数GARCH模型的收敛估计方法。此后，很多学者开始了非参数GARCH模型的实证研究[19-22]。与非参数GARCH模型相比，将非参数的思想与CARR模型相结合而进行的研究就非常少了。目前，只有王敏等[23]在其硕士论文中以沪深300指为研究对象，建立了参数、非参数CARR(1,1)模型，并且证实了非参数CARR(1,1)模型的拟合度高于参数CARR(1,1)模型。

尽管非参数模型能得到非常接近真实值的估计值，但是该模型的解释能力非常弱，这是因为非参数模型不能得到有关函数形式的任何信息。所以为了同时保留非参数CARR模型不依赖于模型形式和参数CARR模型中参数对模型的解释作用这两个优点，有必要建立半参数CARR模型。

半参数模型是介于参数和非参数模型之间的一种过渡模型。通过比较这3种模型，可知半参数和非参数模型都避免了参数模型依赖于模型形式这一缺陷，同时，半参数模型还保留了参数模型中参数对模型具有解释作用这一优点，而非参数模型不具备该能力，使得该模型逐渐成为了学者研究的热点[24-27]。

半参数模型的一般形式为：

(2)

其中：g为R1上的未知函数；B为p维待估参数向量；εi为独立同分布的随机变量，均值为0，具有有限的方差σ2。相对来说，针对式(2)的性质及其估计方法的文章就有所减少了。Shi Peide等[28]考虑了固定设计下该模型的估计问题。国内学者柴根象等[29]基于模型的可加性估计出了模型的参数。赵选民等[30]对该模型的非参数部分采用核估计方法，获得了非参数函数的最优收敛估计量。与前述两种研究方向相比，将式(2)设定为波动性模型进行研究的文章就非常之少了，而且研究中所采用的波动性模型仅限于GARCH模型。国内学者陆书芳[31]以上证综指为研究对象建立了半参数GARCH模型来研究上海证券市场的波动性；国外学者Gallant[32]提出了基于半参数GARCH模型的最大线性估计方法；Shin[33]提出了半参数GARCH(1,1)-M模型；Yang[34]针对汇率交换市场的波动性建立了半参数GARCH模型。Yang等[35]提出了半参数 EGARCH 模型，并将其用于中国股票市场的实证分析中。

目前，还鲜有文献对半参数CARR模型进行研究。据上述相关文献中非参数模型和半参数模型的阶数设定经验，本文建立了一阶非参数和半参数CARR模型对上海证券市场的波动性进行研究，并对参数CARR模型、非参数CARR模型和半参数CARR模型的拟合能力进行了比较。

2 参数、非参数和半参数CARR(1,1)模型介绍

2.1参数CARR(1,1)模型

在模型形式和性质方面，参数CARR模型类似于GARCH模型以及ACD模型。CARR(1,1)模型如式(3)所示：

(3)

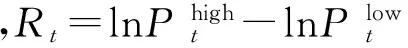
2.2 非参数CARR(1,1)模型

非参数CARR(1,1)模型只包含一般的函数形式：

(4)

式(4)中的Rt、λt、εt所表示的内容同式(3)，只是在非参数CARR(1,1)模型中并不要求εt服从某一特定的分布。式(4)与式(3)最大的区别在于引入了一个光滑但未知的函数m(·)。估计模型中函数m(·)是拟合非参数CARR(1,1)模型最主要的问题。

2.3 半参数CARR(1,1)模型

半参数CARR(1,1)模型包括简单的参数CARR模型的形式，同时又引入了更一般的函数形式。半参数CARR(1,1)模型形式如式(5)：

(5)

式(5)中，Rt、λt、εt、α所表示的内容同式(3)，只是在半参数CARR(1,1)模型中并不要求εt服从某一特定的分布。同参数CARR(1,1)模型相比，α的存在增加了半参数CARR(1,1)模型的解释能力。式(5)与式(3)最大的区别在于引入了一个光滑但未知的函数m(·)。估计模型中的α和函数m(·)是拟合半参数CARR(1,1)模型最主要的问题。

3 非参数、半参数CARR(1,1)模型的估计算法

3.1非参数CARR(1,1)模型的估计

为了估计非参数CARR(1,1)模型，必须对式(4)进行变形，变形之后的形式如式(6)所示：

Rt=m(Rt-1,λt-1) +ξt

(6)

其中：ξt=m(Rt-1,λt-1)(εt-1)，且ξt是期望为0、相互独立的条件异方差过程。一般的非参数模型的估计方法主要有核估计、邻近估计、局部线性估计、样条估计等，这些估计方法都比较成熟。其中核估计和局部线性估计因其原理简单易懂且可操作性强被经常使用，但是核估计存在边界效应，估计结果的误差会大于局部线性估计结果的误差，所以局部线性估计方法的使用率更高于核估计方法。考虑到式(6)中含有未知变量λt-1，不同于一般的非参数模型，需采用迭代算法求出未知函数的渐进估计。综合考虑，本文将局部线性估计嵌套到迭代算法中来估计最终的模型。

迭代过程如下：

第1步：采用极大似然估计方法估计基于标准指数、weibull分布、gamma分布下的参数CARR(1,1)模型中的参数，从中选择最优模型，以该最优模型的极差的条件期望{λt,0;1≤t≤n}为半参数模型中的λt-1的初始值，此时设迭代次数j=1。

第2步：用{Rt;2≤t≤n+1}对{Rt;1≤t≤n}和第一步得到的{λt,0;1≤t≤n}做非参数回归，此时非参数回归采用二元局部线性回归估计，该估计通过式(7)实现：

Kh1(Rt-1-R)Kh2(λt-1-λ)

(7)

其中：K(·)为核函数；h为带宽。

第4步：将迭代次数j的值加1返回第2步，持续到估计结果稳定时为止。

研究以上步骤可以发现：如何进行局部线性估计是整个迭代过程的核心问题。

3.2 半参数CARR(1,1)模型的估计

为了估计半参数CARR(1,1)模型，必须对式(5)进行变形，变形之后的形式如式(8)所示：

Rt=αRt-1+m(λt-1) +ξt

(8)

其中：ξt=Rt-λt，ξt是一个期望为0、相互独立、条件异方差过程。

一般的半参数模型的估计方法主要有最小二乘核估计、最小二乘邻近估计、最小二乘局部线性估计等。其中，最小二乘局部线性估计因其原理简单易懂且可操作性强被经常使用。考虑到式(8)中含有未知变量λt-1，不同于一般的半参数模型，需采用迭代算法求出参数和未知函数的渐进估计。综合考虑，本文将最小二乘局部线性估计嵌套到迭代算法中来估计最终的模型。

具体的运算步骤如下：

第1步：采用极大似然估计方法估计基于标准指数、weibull分布、gamma分布下的参数CARR(1,1)模型中的参数，从中选择最优模型，以该最优模型的极差的条件期望{λt,0;1≤t≤n}为半参数模型中的λt-1的初始值，此时设迭代次数j=1。

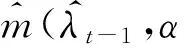
第4步：将迭代次数j的值加1返回第2步，持续到估计结果稳定时为止。

研究以上步骤可以发现：最小二乘局部线性估计实质上是局部线性估计和最小二乘估计相结合而形成的一种方法。其中，最小二乘法是计量经济研究中最常用的方法，在此不作赘述。所以，同非参数CARR(1,1)的估计方法一样，如何进行局部线性估计是拟合半参数CARR(1,1)模型的核心问题。

3.3 局部线性估计

局部线性估计是局部多项式估计的特殊情况。

设变量Y,X，且变量Y与X之间的回归关系为y=m(x)，回归函数m(x)在x0的一个邻域内有连续的p阶导数，利用Taylor公式将m(x)在x0处展开：

(9)

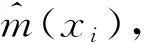
运用最小局部加权平方和的方法估计出βj，计算公式如下：

(10)

其中：n为样本数；k(·)表示核函数；h表示带宽；β0=m(xr)；β1=m′(xr)。经过计算可以得到：

(11)

其中：

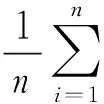
(12)

衡量估计精度的常用指标为均方误差(mean square error， MSE)

(13)

其中

(14)

(15)

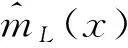
3.3.1 核函数的选取原则

在理论上，核函数必须为高阶函数族，而且具备对称性，即满足：

(16)

证明见文献[36]。

从以上理论可知：核函数不一定是密度函数。但是在应用中，一般选取密度函数为核函数，这是因为选取密度函数作为核函数进行估计，估计精度更高。常见的核函数有Boxcar、Gaussian、Epanechnikov、Tricube。而核函数的性能通常是通过渐进均方误差(asymptotic integral mean square error，AMISE)来衡量的，核函数Epanechnikov能使AMISE达到最小[37]，所以本文选取Epanechnikov作为核函数。

3.3.2 带宽的选取原则

由式(14)、(15)可知：带宽过大意味着过度平均化，会掩盖分布的局部特征，造成较大的偏差；带宽过小会增加随机效应，造成较大的方差。鉴于此，需选取最优带宽来权衡偏差与方差。理论上，最优带宽的确定主要有3种方法，分别是极小化均方误差法(mean square error， MSE)、极小化积分均方误差法(integral mean square error， MISE)和极小化渐进积分均方误差(asymptotic integral mean square error， AMISE)[38]。采用以上3种方法确定最优带宽都需要对密度函数有一定的假设，实际上在进行实证时，数据是随机的，往往存在不满足假设的情况，导致了这3种方法在理论上具备可行性，在实际操作中困难较大。

Allen[39]和Rudemo[40]提出了采用交叉验证法(cross validation，CV)确定带宽。Stone[41]证明了交叉验证法的合理性。CV法是一种数据本源法(data based)，不需要对密度函数假设，但是CV方法计算复杂。Wahba[42]对CV方法进行了改良，提出了广义交叉验证(generalized cross validation，GCV)。

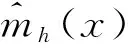
(17)

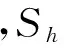
(18)

其中：I表示单位矩阵；tr(·)表示矩阵的迹。最小化GCV可得到所需要的最优带宽。

Parkasa[43]证明了在进行非参数回归估计时，核函数的不同选择对估计结果并不敏感，而相差甚小的带宽的估计结果却差别很大，说明了带宽决定着估计效果的优劣。因此，本文在确定以Epanechnikov为核函数后，再采用GCV方法确定带宽以进行局部线性估计。

4 实证研究

4.1 数据的基本统计特征

本文选取上海证券综合指数(简称上证综指)为研究对象，以该对象的日内最高价与最低价的自然对数之差为样本序列。样本的选取时间段为1990年12月19日至2014年6月18日，总共 5 746个数据。

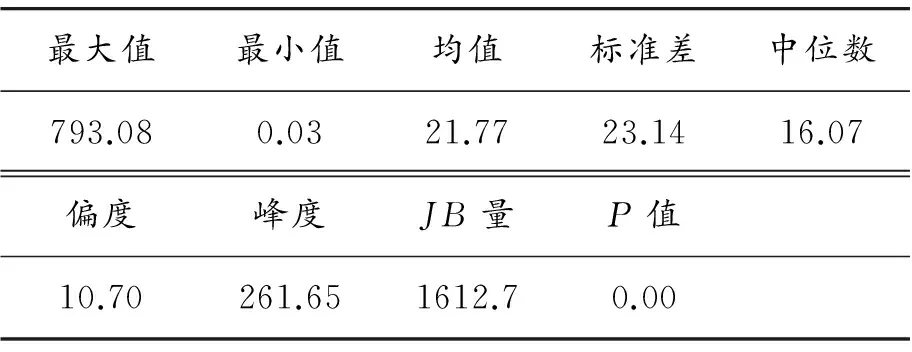
表1 上证综指日对数价格极差序列的基本统计特征

从表1可知：该样本的中位数小于均值，存在明显的右偏现象。针对样本的正态分布特征，本文采用了Jarque-Bera(即JB)统计量来检验。该统计量的值为1 635.395 2，明显拒绝了正态分布的原假设。

表2给出了利用Augmented Dickey-Fuller(ADF)方法对上证综指日对数价格极差序列的平稳性检验的结果。

表2 上证综指日对数价格极差序列的平稳性检验结果

从检验结果看，在1%、5%、10% 3个显著性水平下，单位根检验的临界值分别是-3.431 3、-2.861 8、-2.567 0，均大于相应临界值，从而拒绝原假设，表明上证综指日对数价格极差序列不存在单位根，是平稳序列。

4.2 参数CARR(1,1)模型的建模

假设参数CARR(1,1)模型中的残差项分别服从标准指数分布、Weibull分布和Gamma分布，以平稳的上证综指日对数价格的极差序列为样本数据建立参数CARR(1,1)模型，见表3。

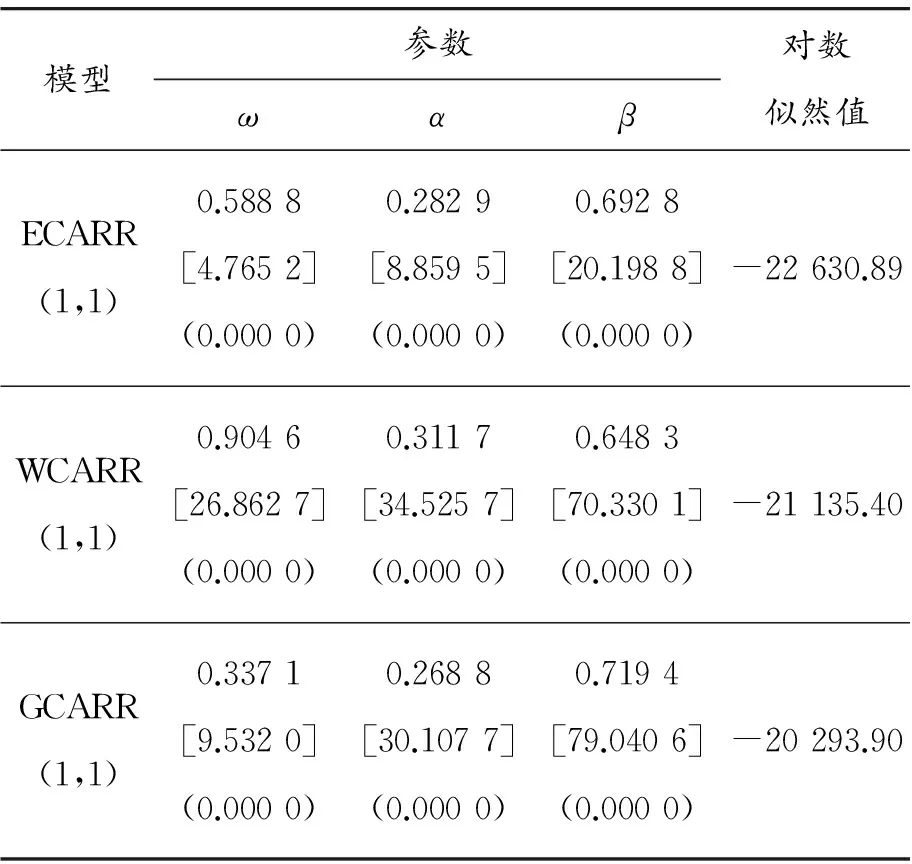
表3 参数CARR(1,1)模型的估计结果

注：[ ]中是参数的t统计量，( )是参数的p值

从表3可以看出：按照最大似然值法，GCARR(1,1)模型的对数似然值最大，并且该模型中的参数可全部通过检验，说明在所建立的3个模型中，GCARR(1,1)模型是最优模型，能贴切地描述上海股票市场的波动性。

4.3 非参数CARR(1,1)模型的建模

以平稳的上证综指极差序列为样本数据建立非参数CARR(1,1)模型，因为非参数CARR(1,1)模型没有具体的函数形式，所以在迭代的过程中只能通过选取误差度量指标来衡量模型的拟合优度。本文选取平均平方误差(MSE)、平均绝对误差(MAE)两种度量指标作为评判标准。

(19)

非参数CARR(1,1)模型的逐次迭代结果如表4所示。

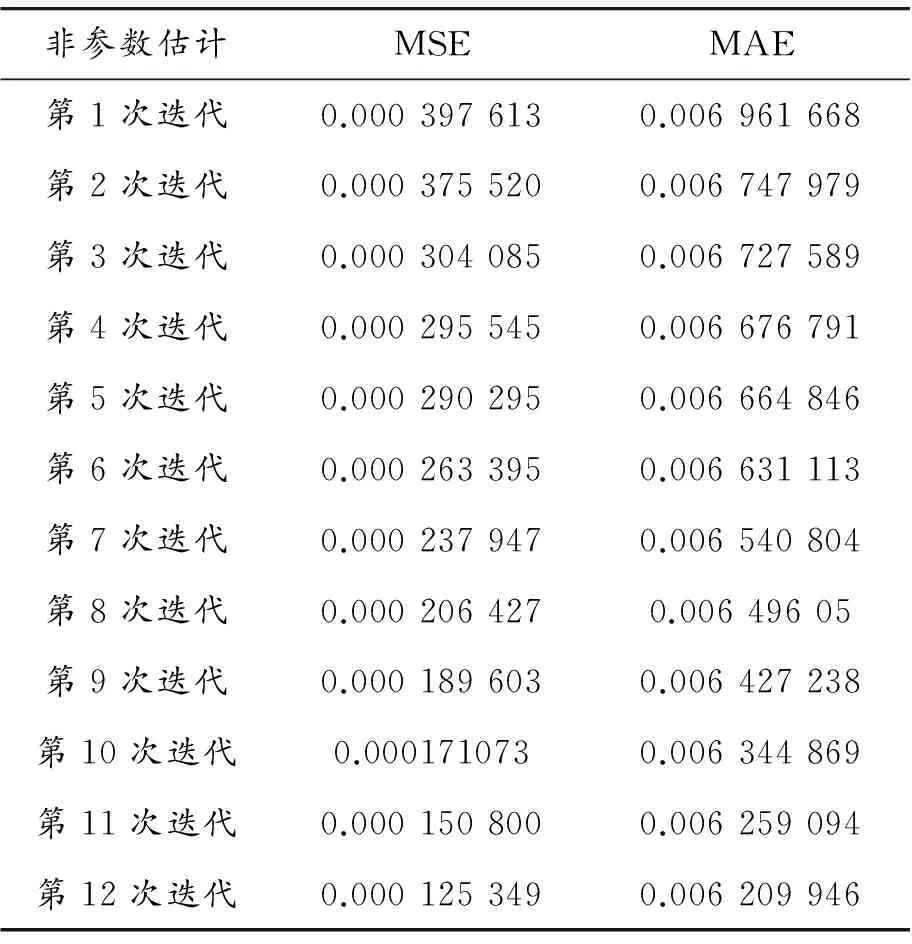
表4 非参数CARR(1,1)的MSE和MAE

从表4可以看出：在迭代的过程中，MSE和MAE的值逐渐变小，说明采用局部线性估计方法进行迭代得到的结果具备稳定性和收敛性。其中，MSE的结果从第1次迭代的0.000 397 613到第12次迭代的0.000 125 349，误差下降了68.47%，12次迭代的平均误差是0.000 250 63。非参数CARR(1,1)模型的MAE的结果从第1次迭代的0.006 961 668到第12次迭代的0.006 209 946，误差下降了10.79%，12次迭代的平均误差是0.006 557 332。

4.4 半参数CARR(1,1)模型的建模

表5 参数α的逐次估计结果

从表5可以看出：以上证综指为样本建立的半参数CARR(1,1)模型中的参数α的估计经过每次迭代后，估计结果都相差不大，说明了该估计方法具备稳定的性质。参数α的取值表示极差的滞后期对极差的条件期望的影响程度，表5中参数α的估计结果可以说明极差的滞后期对极差的条件期望的影响不是很大。

同样以MSE和MAE为误差度量指标，半参数CARR(1,1)模型在迭代的过程中误差变化如表6所示。

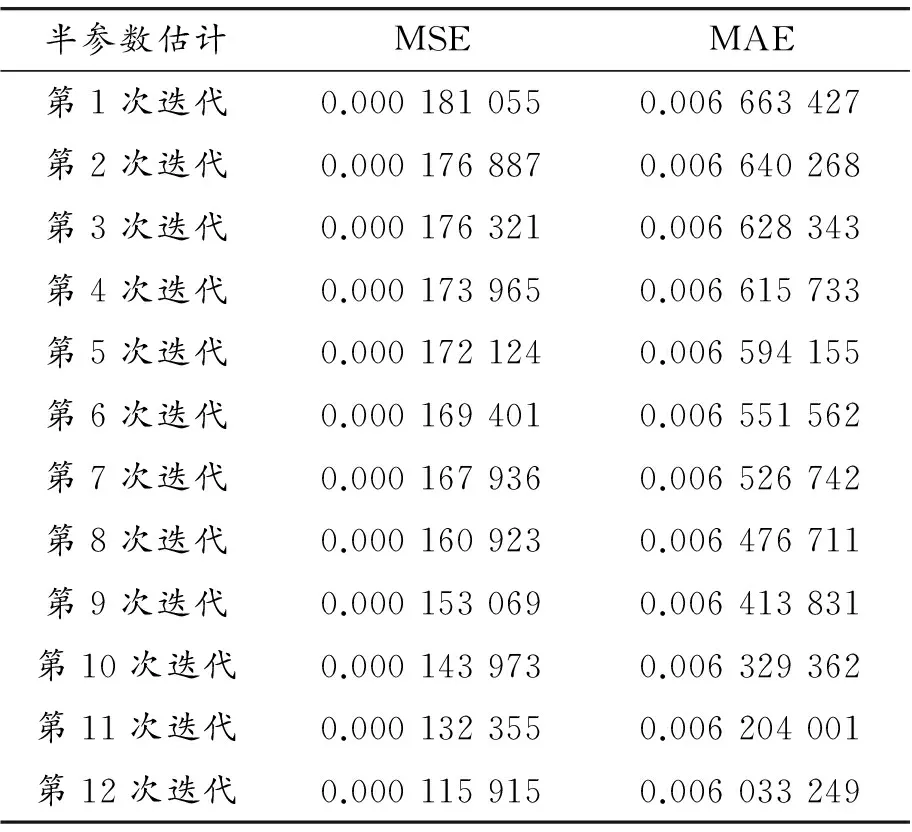
表6 半参数CARR(1,1)的MSE和MAE

从表6所示的MSE和MAE的结果可以看出：半参数CARR(1,1)模型的估计值与真实值之间的误差经过逐次迭代后，估计结果逐渐趋于稳定。MSE的结果从第1次迭代的0.000 181 055到第12次迭代的0.000 115 915，误差下降了35.97%，12次迭代的平均误差是0.000 160 327。半参数CARR(1,1)模型的MAE的结果从第1次迭代的0.006 663 427到第12次迭代的0.006 033 249，误差下降了9.45%，12次迭代的平均误差是0.006 473 115。

4.5 模型的拟合能力评价

图1～3分别表示了GCARR(1,1)、非参数CARR(1,1)、半参数CARR(1,1)模型的实际值与估计值之间的对比。

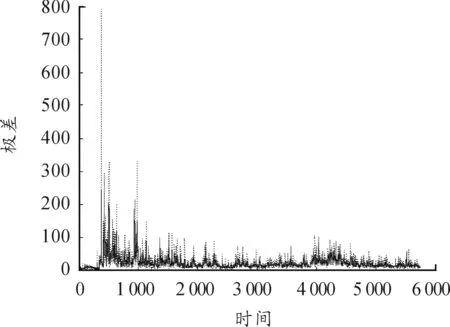
图1 GCARR(1,1)的真实值与估计值对比

图2 非参数CARR(1,1)的真实值与估计值对比

图3 半参数CARR(1,1)的真实值与估计值对比

为了更精确地判别参数GCARR(1,1)、非参数、半参数CARR(1,1)模型哪个可以更好地拟合上海证券市场的波动性，本文对比了这3个模型的MSE和MAE。

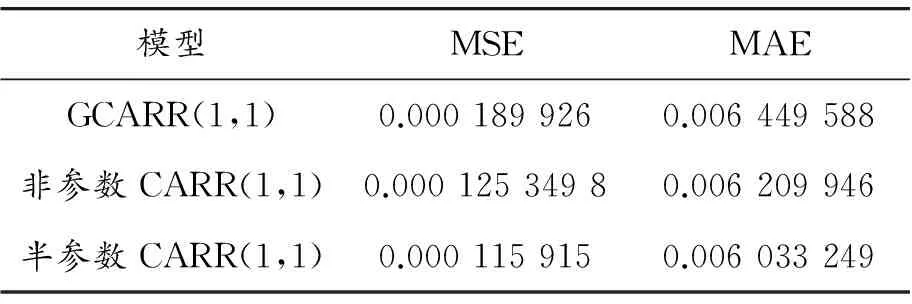
表7 参数GCARR(1,1)、非参数、半参数CARR(1,1)的MSE和MAE

表7通过比较MSE和MAE可知：GCARR(1,1)模型的估计值与真实值之间的差异最大。通过比较非参数CARR(1,1)和半参数CARR(1,1)可知：半参数(1,1)的拟合优度高于非参数CARR(1,1)模型，说明在以上证综指日对数价格的极差为研究对象时，半参数CARR(1,1)模型比非参数CARR(1,1)模型更加稳定。所以，半参数CARR(1,1)的拟合优度最高，非参数CARR(1,1)次之，参数GCARR(1,1)拟合优度最差，说明了半参数CARR(1,1)最适合描述上海股票市场的波动性。

5 结束语

本文基于参数、非参数和半参数CARR(1,1)模型讨论了上海股票市场的波动性，实证分析结果表明：

1) 本文采用迭代算法进行非参数、半参数CARR(1,1)模型拟合时，每次拟合的结果都相差不大，说明本文采用的估计方法具有比较稳定的性质。

2) 通过实证得出的MSE和MAE可知：在所建立的3种模型中，半参数CARR(1,1)模型是拟合优度最高的模型。在对上证综指日对数价格的极差数据进行半参数模型拟合时，趋于稳定的非参数部分拟合的曲线大致呈直线形式，说明极差的条件期望的滞后期以线性的方式影响着极差的条件期望的函数形式。 3) 无论是参数、非参数还是半参数CARR(1,1)模型都说明了上海股票市场的波动具有聚集性和持续性。

[1] ENGLE R F.Auto-regressive Conditional Heteroscedasticity with Estimates of The Variance of United Kingdom Inflation[J].Econometrics,1982,50(4):987-1007.

[2] BOLLERSLEV T.Generalized Auto-regression Conditio-nal Heteroscedasticity[J].Journal of Business,1986,31(3):307-327.

[3] PARKINSON M.The Extreme Value Method for Estimating the Variance of The Rate of Return[J].Journal of Business,1980(53):61-65.

[4] CHOU R Y.Forecasting financial Volatility with Extreme Values:the Conditional Auto-regressive Range(CARR) Model[J].Journal of Money,Credit and Banking,2005,37(3):561-582.

[5] CHOU Heng-chih,WANG David.Using Conditional Auto-regressive Range Model to Forecast Volatility of the Stock Indices[C]//Proceedings of the 2006 Joint Conference on Information Science Kaohsiung. Taiwan,2006.

[6] 程细玉,夏天.金融市场波动性CARR类模型与GARCH类模型的比较研究[J].数学的实践与认识,2009,39(13):12-18.

[7] 张苏林.我国黄金现货波动率预测能力分析——基于GARCH模型与CARR模型的比较[J].金融理论与实践,2011(8):47-50.

[8] 耿立艳,马军海.运用最小二乘支持向量回归机和CARRX模型对股市波动率的预测[J].统计与决策,2008(13):48-50.

[9] 卢米雪.基于CARR-X模型的股市高频环境下量价关系动态研究[J].求索,2013,12:22-24.

[10] RAY C,WU C C,SAM H,et al.Estimating Value at Risk with A Dynamical Conditional Range Model[D].[s.l.]:European Financial Management Association (EFMA),2007.

[11] CHOU H C,DAVID W.Estimation of Tail-Related Value at Risk Measures[J].Quantitative Finance,2013,13(2):293-304.

[12] 赵树然,任培民,赵昕.基于CARR-EVT整体方法的动态日VaR和CVaR模型研究[J].数量经济技术经济研究,2009(11):130-148.

[13] WAND M P,JONES M C.Kernel Smoothing Chapman and Hall[M].Boca Raton:CRC Press,1995.

[14] FAN.Local Linear Regression Smoothers and Their Minimax Efficiencies[J].The Annals of Statistics,1993,21(1):196-216.

[15] FAN J,GIJBELS I.Local Polynomial Modelling and Its Applications[M].London:Chapman and Hall,1996.

[16] GREEN S.Non-parametric Regression and Generalized Linear Models[M].London:Chapman and Hall,1994.

[17] STONE,MARK H,CHARLES K,et al.The Use of Polynomial Splines and Their Tensor Products in Extended Linear Modeling (with discussion)[J].Annals of Statistics,1997,25:1371-1470.

[18] BÜHLMANN P,MCNEIL A J.An Algorithm for Non-parametric GARCH Modeling[J].Computational Statistics & Data Analysis,2002,40:665-683.

[19] FRANCQ C， ZAKOIAN J.Mixing Properties of A General Class of GARCH(1,1) Models without Moment Assumptions on The Observed Process[J].Econometric Theory,2006,5(22):815-835.

[20] HOU A J,SANDY S.A Non-parametric GARCH Model of Crude Oil Price Return Volatility[J].Energy Economics,2012,34(2):618-626.

[21] 鲁万波.基于非参数GARCH模型的中国股市波动性预测[J].数理统计与管理,2006,25(4):455-461.

[22] 张华高.基于非参数GARCH-M模型金融市场波动性研究[D].上海:复旦大学,2010.

[23] 王敏,鲁万波.非参数条件自回归极差模型及其应用[D].成都:西南财经大学,2013.

[24] LE Cam L,YANG G L.Asymptotic in Statistics:Some Basic Concepts[J].Springer,1990.

[25] BICKEL P J,KLAASSEN C A J,RITOV Y,et al.Efficient and Adaptive Estimation for Semi-parametric Models[J].The Indian Journal of Statistics,1993,62:157-160.

[26] ANDERSEN P K,BORGAN O,GILL R D,et al.Statistical Models Based on Counting Processes[J].Siam Review,1995,37(03):767.

[27] PETER J B,JAIMYOUNG K.Inference for Semi-parametric Models:Some Questions and An Answer[J].Statistica Sinica,2011,(11):863-960.

[28] SHI P,TENG X D.Asymptotic Distributions of M-estimators of The Parametric Components of Partly Linear Models with Fixed Carriers[J].Advances in Mathematics,1999,28(5):447-461.

[29] 柴根象,孙平,蒋译云.半参数回归模型的二阶段估计[J].应用数学学报,1995,18(3):353-363.

[30] 赵选民，魏新宇.半参数回归模型的渐进有效L-估计[J].系统科学与数学,2003,23(1):136-144.

[31] 陆书芳.基于半参数GARCH模型的上证指数实证分析[J].重庆工商大学学报(自然科学版),2013,30(6):6-15.

[32] GALLANT A R,NYCHKA D W.Semi-parametric Maximum Likelihood Estimation[J].Econometric,1987,55:363-390.

[33] SHIN J.Stock Returns and Volatility in Emerging Stock Markets[J].International Journal of Business and Economics,2005,4(1):31- 43.

[34] YANG L.A Semi-parametric GARCH Model for Foreign Exchange Volatility[J].Journal of Econometric,2006(130):365-384.

[35] YANG H,WU X.Semi-parametric EGARCH Model with The Case Study of China Stock Market[J].Economic Modeling,2011,28(3):761-766.

[36] 朱干江.非参数密度估计在判别分析中的应用[D].南京:南京信息工程大学,2007.

[37] 牛君.基于非参数密度估计点样本分析建模的应用研究[D].济南:山东大学,2007.

[38] 王星.非参数统计[M].北京:清华大学出版社,2009.

[39] ALLEN D M.The Relationship between Variable Selection and Data Augmentation and A Method for Prediction[J].Technometrics,1974,16:125-127.

[40] RUDEMO M.Empirical Choice of Histogram and Kernel Density Estimators[J].Scandinavian Journal of Statistics,1982(9):65-78.

[41] STONE C J.An Asymptotically Optimal Window Selection Rule for Kernel Density Estimates[J].Annals of Statistics,1984(12):1285-1297.

[42] WAHBA G.The Approximate Solution of Linear Operator Equations When The Data Are Noisy[J].SIAM Journal on Numerical Analysis,1977(14):651-667.

[43] PARKASA.Non-parametric Function Estimation[M].London:Academic Press,1983.

(责任编辑何杰玲)

NonparametricandSemiparametricCARRModelsforShanghaiStockMarketVolatility

GUO Mingyuan, HAN Zhinan

(College of Management and Economics, Tianjin University, Tianjin 300072, China)

2016-02-24

国家社会科学基金资助项目(14CTJ012)

郭名媛(1979—)，女，天津人，博士，副教授，硕士生导师，主要从事金融系统分析研究，E-mail：leu2@163.com；韩志楠(1991—)，女，山西临汾人，硕士研究生，主要从事金融时间序列分析研究。

郭名媛，韩志楠.基于非参数和半参数CARR模型的上海股票市场波动性研究[J].重庆理工大学学报(自然科学)，2017(9):172-181.

formatGUO Mingyuan, HAN Zhinan.Nonparametric and Semiparametric CARR Models for Shanghai Stock Market Volatility[J].Journal of Chongqing University of Technology(Natural Science)，2017(9):172-181.

10.3969/j.issn.1674-8425(z).2017.09.027

O21;F830

A

1674-8425(2017)09-0172-10