聚焦条件下菲涅尔圆孔衍射合振动的积分式及应用

(长江大学物理与光电工程学院，湖北 荆州 434023)

聚焦条件下菲涅尔圆孔衍射合振动的积分式及应用

苏海涛

(长江大学物理与光电工程学院，湖北荆州434023)

运用惠更斯-菲涅尔原理，分析了轴线点光源在聚焦条件下的菲涅尔圆孔衍射，通过对平行次波间光程差的计算，计算出各次波在会聚点的光程，由此导出了上述条件下衍射合振动的积分式。这一积分式在一定条件下(小张角时)，可以求出其原函数，这为合振幅(光强)计算带来了很大的方便。由于夫琅禾费圆孔衍射相当于点光源距离圆孔很远时的菲涅尔圆孔衍射，完全符合小张角的条件，由这一函数式导出了夫琅禾费圆孔衍射合振动的函数式。

聚焦；菲涅尔圆孔衍射；合振动；积分式；函数式

在传统光学教材中，聚焦条件下夫琅禾费圆孔衍射合振动积分式的推导并解出原函数，是一个数学的范例[1]。对菲涅尔圆孔衍射合振动的研究现在普遍处于非聚焦条件下，主要分2种情况，一是非聚焦条件下合振动积分式的推导并在特殊条件下解出原函数[2]；二是非聚焦条件下合振动积分式的数值计算[3～6]。由以上原函数与数值计算所得到的合振幅(亦即光强)分布，对应于直接在光屏上形成的衍射图样，但它不能对应于经光学系统或人眼后的成像(衍射图样)；而聚焦条件下菲涅尔圆孔衍射的合振幅分布则对应于经光学系统或人眼后的成像，有更大的应用意义。笔者的研究旨在解决聚焦条件下菲涅尔圆孔衍射合振动的计算问题。夫琅禾费圆孔衍射可以看作菲涅尔圆孔衍射的一个特例，笔者分析了轴线点光源在聚焦条件下的菲涅尔圆孔衍射，并导出了其合振动的积分式，在小张角的条件下这一积分式可以解出原函数，夫琅禾费圆孔衍射合振动的函数式就可以由这一原函数导出。

1 聚焦条件下的菲涅尔圆孔衍射分析

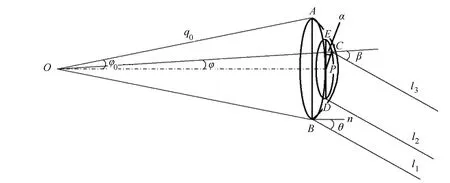
图1 菲涅尔圆孔衍射的光路分析

如图1所示，点光源O发出的球面波经圆孔产生衍射，点O位于小孔的中心轴线上，AB为圆孔直径。点光源对圆孔的张角∠AOB=2φ0，OA=OB=q0。DE为平行于圆孔面的球冠截面的直径，且DE∥AB，P为该截面的圆心。显然，OP为圆孔中心轴。C为该截面圆周上的任意一点，l1、l2、l3为透过圆孔的波面发出的3列次波，相互平行。次波l1的波源为B点，它与圆孔面法线n的夹角(即衍射角)为θ；次波l2的波源为D点；次波l3的波源为C点，∠COP=φ， ∠CPE=α。波线l1、l2位于经过圆孔中心轴的截面OAEDB内。

图2 l3与l2的光程差分析示意图

衍射角为θ的各平行次波经透镜会聚于观察点，计算它们到达会聚点的光程时以l1的光程为比较，l3与l1的光程差等于l3与l2的光程差加上l2与l1的光程差。

先计算l3与l2的光程差。如图2所示，过C点作CF⊥DE，过F作l4∥l3，可以证明l3与l2的光程差等于l4与l2的光程差[1]。由OD=OE=q0、三角关系以及空气的折射率近似等于1，算得l4与l2的光程差为：

δ1=q0sinφ(1+cosα)sinθ

(1)

再计算l2与l1的光程差。图3是包括l1与l2的球扇形的轴截面图，图中BF⊥l2，DF即为l2与l1的光程差。令δ2=DF，可求得：

δ2=q0[cos(φ0-θ)-cos(φ-θ)]

(2)

于是次波l3与l1的光程差：

δ=δ1+δ2=q0sinφ(1+cosα)sinθ+q0cos(φ0-θ)-q0cos(φ-θ)

(3)

图3 l2与l1的光程差分析示意图

2 合振动的积分式

设次波l1到达观察点的光程为s(θ)，则次波l3到达观察点的光程为：

RC=s(θ)+δ=s(θ)+q0sinφ(1+cosα)sinθ+q0cos(φ0-θ)-q0cos(φ-θ)

(4)

则C点的面元ds发出的次波l3到达观察点的振动可表示为：

dyC=C0cos[ωt-kRC]ds

(5)

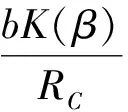
(6)

将式(4)代入式(6)，得到波面上沿θ方向的各次波经透镜会聚于观察点的合振动的积分式：

(7)

3 小张角时菲涅尔圆孔衍射合振动的函数式

C0影响着合振动振幅极值的大小和位置，在φ0与θ不大的情况下，β、RC随θ、φ、α的变化不大，从而使得C0随θ、φ、α的变化不大，因此在近似的情况下，C0可以取常数(依然以C0表示)。在C0取常数时，可以用数值方法算出式(7)合振动的振幅分布，而在以下条件下，则能完成积分，求出式(7)的原函数。

当2φ0为小角时，sinφ0≈φ0、cosφ0≈1、sinφ≈φ、cosφ≈ 1，代入式(7)并将cos(φ0-θ)展开得：

(8)

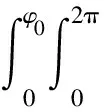
(9)

由此得到小张角时菲涅尔圆孔衍射合振动的函数式：

y=H0cos[ωt-ks(θ)-kq0φ0sinθ]

(10)

4 夫琅禾费圆孔衍射合振动的函数式

夫琅禾费圆孔衍射相当于光源距离很远时的菲涅尔圆孔衍射，满足2φ0→0，且此时q0φ0=r(r为衍射圆孔的半径)，于是由式(10)得到夫琅禾费圆孔衍射合振动的函数式：

y=H0cos[ωt-ks(θ)-krsinθ]

(11)

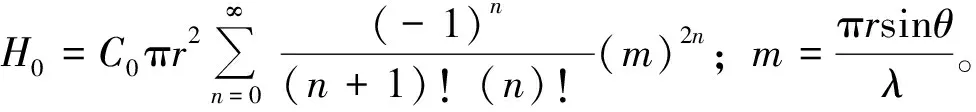
5 结语

推导聚焦条件下菲涅尔圆孔衍射合振动的积分式的关键在于平行次波间光程差的计算，由此可以算出各平行次波在会聚点的光程。实际上，倾斜因数K(β)完全可以近似地等于cosβ，使积分表达式(7)成为具有确定函数形式的计算式，从而进行严格的数值计算。由积分表达式(7)可以导出小张角时菲涅尔圆孔衍射合振动的函数式，由这一函数式可以直接导出夫琅禾费圆孔衍射合振动的函数式，这对传统光学教材中的相关内容是一个很好的补充。

[1]母国光，战元龄. 光学(第二版)[M].北京：高等教育出版社，2009:218～221.

[2]孙景亭. 菲涅尔圆孔衍射[J].天津理工学院学报，1995，11(2)：38～43.

[3]常山，毛杰健，桑志文，等. 单色点源圆孔衍射的数值模拟实验[J].实验室研究与探索，2010，29(6):14～17.

[4]Teng Shuyun，Li Guanghua，Zhang Chong，et al.The diffraction by a small aperture[J].OPTIK，2013，124(16):2507～2510.

[5]陈丽娜，陆霁，朱伟玲. 基于Matlab对菲涅耳圆孔衍射的模拟[J].实验室科学，2014，17(4)：112～115.

[6]何孝卫，杨丽婷，杨光富，等. 圆孔菲涅耳衍射的蒙特卡罗数值模拟[J].云南大学学报(自然科学版)，2014，12(S2):208～212.

[编辑]洪云飞

2017-08-12

苏海涛(1966-)，男，讲师，现主要从事物理基本理论与实验方面的教学与研究工作；htsu@yangtzeu.edu.cn。

引著格式苏海涛.聚焦条件下菲涅尔圆孔衍射合振动的积分式及应用[J].长江大学学报(自科版)，2017,14(21)：69～71.

O436.1

A

1673-1409(2017)21-0069-03