让学生经历真正的建模历程*
——源于三道高三调研测试应用题的深度比较分析
曾 荣
(南通市教育科学研究院 226001)
1 问题提出
数学建模是对现实问题进行数学抽象,用数学语言表达问题、用数学知识与方法构建模型解决问题的素养.高考中对数学建模素养的考查主要体现在应用题的考查上.笔者每年要组织、参加几次市级调研试卷的命题、阅卷、分析工作,发现学生在解答应用题的过程中受到诸多因素的影响,有内部因素,如知识基础、信念动机、解题策略等;也有外部因素,如问题情境、试题类型、设问方式等.其中问题的设问方式往往体现了试题的建模要求,对解答应用题产生了较大影响.本文结合三道高三调研测试应用题的深度比较,尝试说明设问方式对应用题解答的影响,并提出相关教学建议.
2 深度比较
2.1 试题再现
题1(2016江苏南通第三次调研测试)某宾馆在装修时,为了美观,欲将客房的窗户设计成半径为1 m的圆形,并用四根木条将圆分成如图所示的9个区域,其中四边形ABCD为中心在圆心的矩形.现计划将矩形ABCD区域设计为可推拉的窗口.
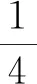
(2)若四根木条总长为6 m,求窗口ABCD面积的最大值.
评注本题的创作灵感来自于笔者命题时住宿的宾馆的窗户,左图为实物图形.问题的背景源于生活实际,促使学生在学习和实践中形成和发展数学应用的意识,同时这样的背景也可保证试题的公平性.
题2(2017江苏南通第一次调研测试)如图,某机械厂要将长6 m,宽2 m的长方形铁皮ABCD进行裁剪.已知点F为AD的中点,点E在边BC上,裁剪时先将四边形CDFE沿直线EF翻折到MNFE处(点C,D分别落在直线BC下方点M,N处,FN交边BC于点P),再沿直线PE裁剪.

题2图

(2)若使裁剪得到的四边形MNPE面积最大,请给出裁剪方案,并说明理由.
评注本题的创作灵感来自于教材中的折纸问题,将其改编成了工程背景的问题.这样的模型学生理解题意方便,建模角度多样,能较好地考查学生的数学建模素养.
题3(2016江苏南通第一次调研测试)如图,阴影部分为古建筑物保护群所在地,其形状是以O1为圆心,半径为1 km的半圆面.公路l经过点O,且与直径OA垂直.现计划修建一条与半圆相切的公路PQ(点P在直径OA的延长线上,点Q在公路l上),T为切点.
(1)按下列要求建立函数关系:
①设∠OPQ=α(rad),将△OPQ的面积S表示为α的函数;
②设OQ=t(km),将△OPQ的面积S表示为t的函数.
(2)请你选用(1)中的一个函数关系,求△OPQ的面积S的最小值.

题3图
评注本题的情境改编自江苏2014年高考应用题,设置方式则参考了江苏2008年江苏高考应用题,图形改编自普通高中课程实验教材(苏教版)数学必修5第19页例4:
如图所示,已知半圆的直径AB=2,点C在AB的延长线上,BC=1,点P为半圆上的一个动点,以PC为边作等边△PCD,且点D与圆心O分别在PC的两侧,求四边形OPDC面积的最大值.

2.2 成绩比较
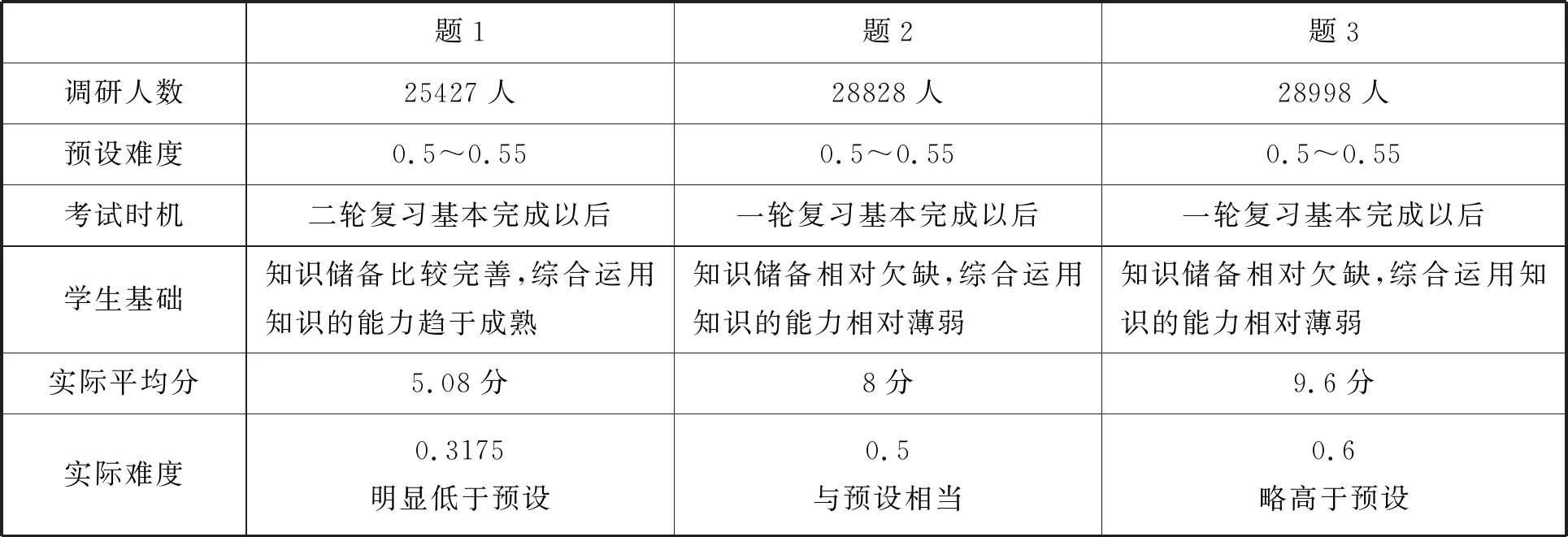
题1题2题3调研人数25427人28828人28998人预设难度0.5~0.550.5~0.550.5~0.55考试时机二轮复习基本完成以后一轮复习基本完成以后一轮复习基本完成以后学生基础知识储备比较完善,综合运用知识的能力趋于成熟知识储备相对欠缺,综合运用知识的能力相对薄弱知识储备相对欠缺,综合运用知识的能力相对薄弱实际平均分5.08分8分9.6分实际难度0.3175明显低于预设0.5与预设相当0.6略高于预设
2.3 试题比较
(1)相同点比较
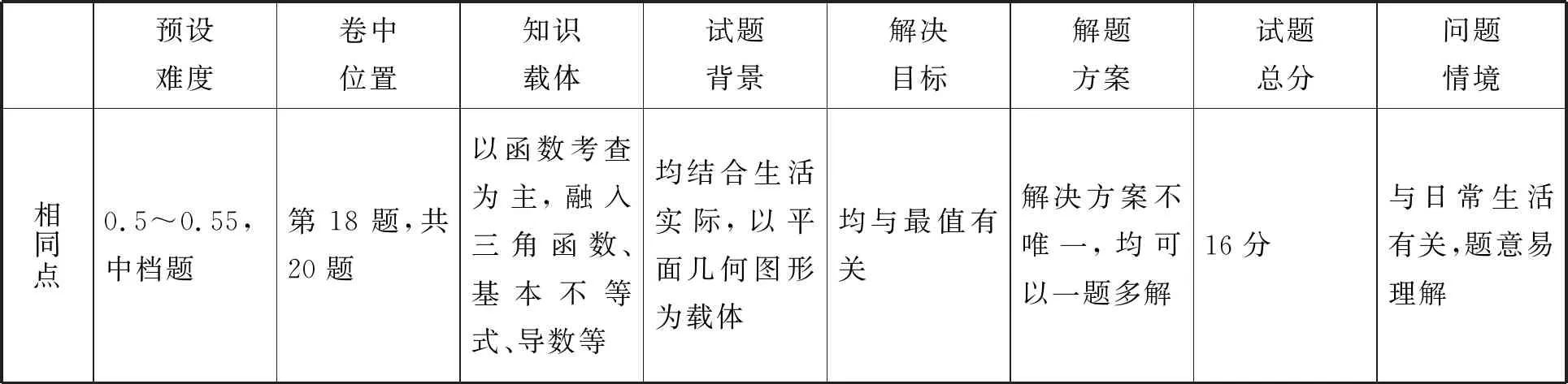
预设难度卷中位置知识载体试题背景解决目标解题方案试题总分问题情境相同点0.5~0.55,中档题第18题,共20题以函数考查为主,融入三角函数、基本不等式、导数等均结合生活实际,以平面几何图形为载体均与最值有关解决方案不唯一,均可以一题多解16分与日常生活有关,题意易理解
(2)不同点比较
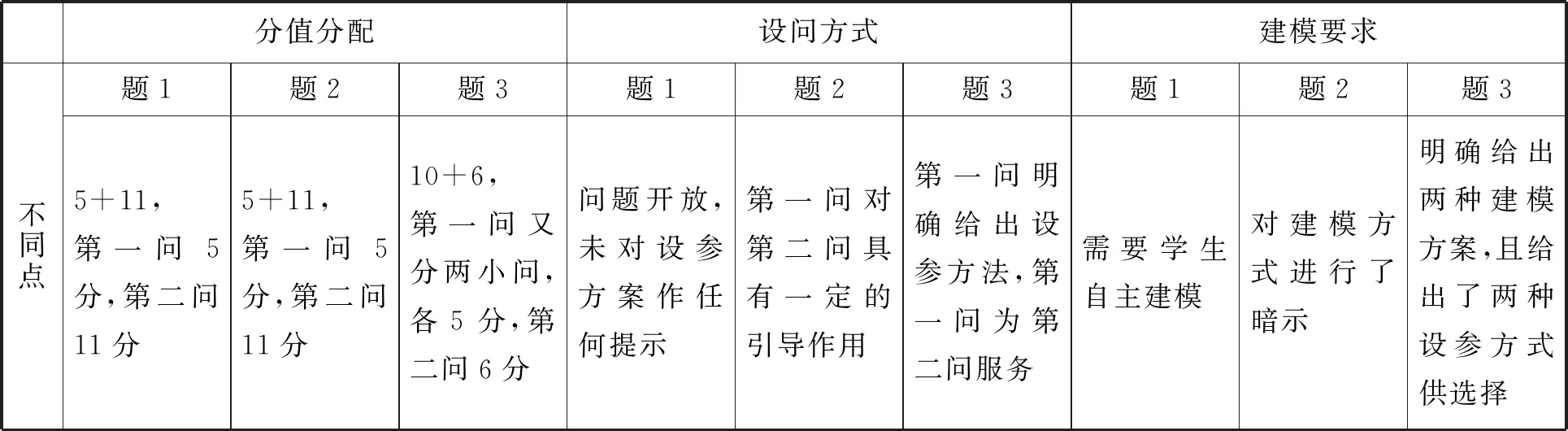
分值分配设问方式建模要求不同点题1题2题3题1题2题3题1题2题35+11,第一问5分,第二问11分5+11,第一问5分,第二问11分10+6,第一问又分两小问,各5分,第二问6分问题开放,未对设参方案作任何提示第一问对第二问具有一定的引导作用第一问明确给出设参方法,第一问为第二问服务需要学生自主建模对建模方式进行了暗示明确给出两种建模方案,且给出了两种设参方式供选择
应用题是高考中影响学生成绩的关键题,解答数学应用题是分析问题和解决问题能力的高层次表现,反映出学生的创新意识、建模能力.通过上面两表的比较可以发现,虽然三道试题在试题考查目标、知识载体、试题难度等方面差异不大,但由于设问方式、建模要求上的差异,造成了巨大的得分差异.由此可见,学生要能解好应用题,必须具备良好的数学建模素养.
3 教学启示
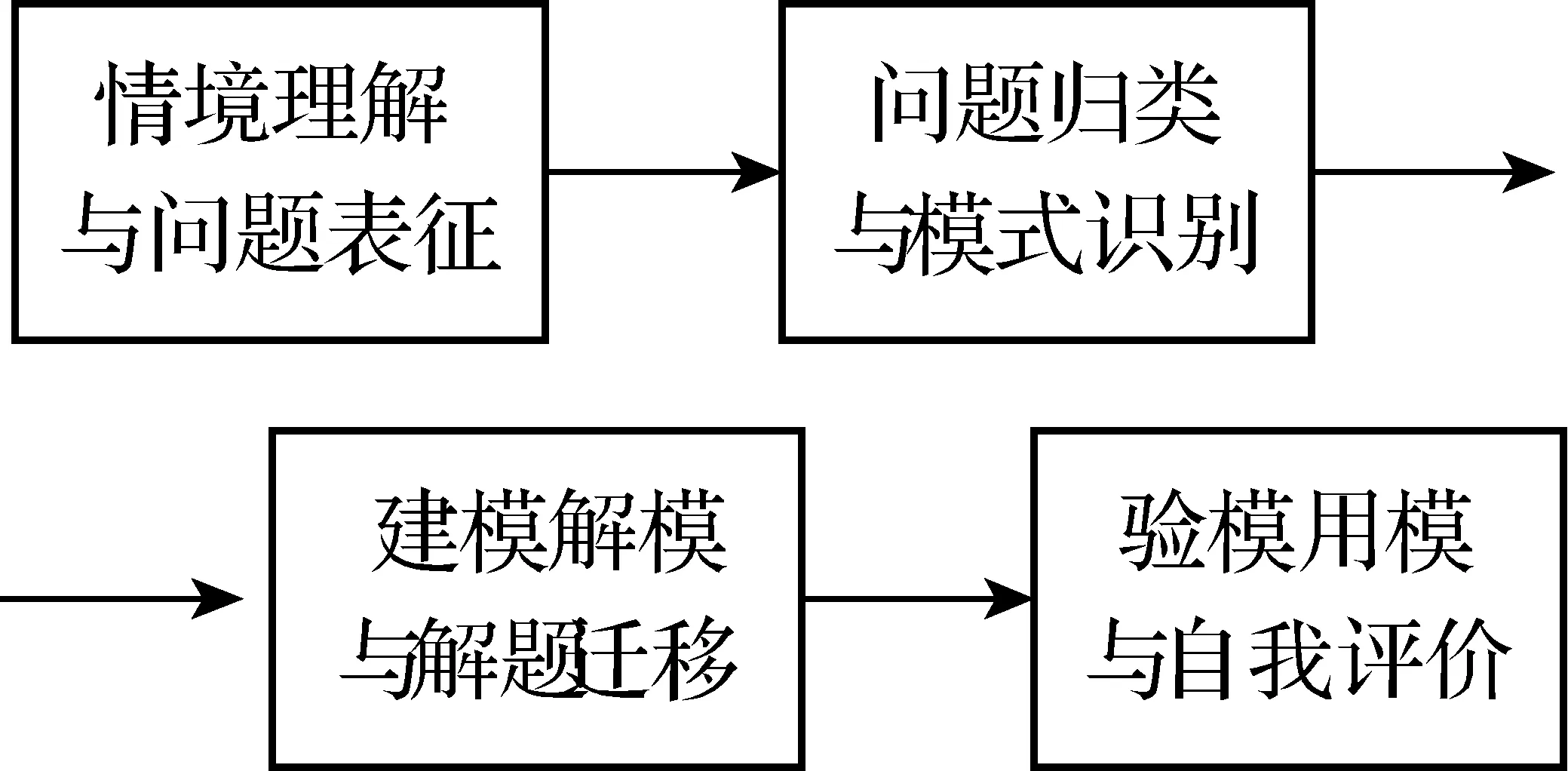
数学应用问题解决的认知过程是主体在数学元认知监控下,摆脱情节结构、建立并处理数量关系结构的一种数学认知活动,由情境理解与问题表征、问题归类与模式识别、建模解模与解题迁移、验模用模与自我评价等4 个相互关联的子系统组成的一个动态过程.
大型考试中,由于考虑到学生基础的差异、考试时间的限制,可能会通过改变设问方式,适当降低对数学建模的要求,如题2、题3.但在日常应用题教学中,我们应立足数学建模素养的培养,把探索实践的机会留给学生,让学生经历真正的建模过程.下面结合题2的处理谈相关教学建议.
3.1 改编设问方式,创设建模机会
在实际教学中,对于应用题的教学,我们不能简单地停留在就题讲题层面,而要善于精选试题,并合理重整加工,改编设问方式,给学生创设真正的建模机会.例如,对于题2,我们可以进行如下的改编.
改编1如图,某机械厂要将长6 m,宽2 m的长方形铁皮ABCD进行裁剪.已知点E在边BC上,BE=2CE,点F在边AD上,裁剪时先将四边形CDFE沿直线EF翻折到MNFE处(点C,D分别落在直线BC下方点M,N处,FN交边BC于点P),再沿直线PE裁剪.试问当点F落在何处时,裁剪掉的四边形MNPE面积最大?

改编1
评注本题可通过折纸实验进行模拟,折叠过程大致分为下图五个环节.从临界位置1到特殊位置,四边形MNPE的面积等于正方形MNHE的面积减去直角三角形EPH的面积,其中正方形MNHE的面积为定值,直角三角形EPH的面积在不断减小,故四边形MNPE的面积在不断增大;从特殊位置到临界位置2,四边形MNPE的面积等于正方形MNHE的面积加上直角三角形EPH的面积,其中正方形MNHE的面积为定值,直角三角形EPH的面积在不断增大,故四边形MNPE的面积在不断增大.故从临界位置1到临界位置2,四边形MNPE的面积一直在增大,在临界位置2处达到最大.这种实验探究法,是解决实际问题的常用方法.

临界位置1一般位置1

特殊位置

一般位置2临界位置2
改编2如图,某机械厂要将长6 m,宽2 m的长方形铁皮ABCD进行裁剪.已知点F为AD的中点,点E在边BC上,裁剪时先将四边形CDFE沿直线EF翻折到MNFE处(点C,D分别落在直线BC下方点M,N处,FN交边BC于点P),再沿直线PE裁剪.若使裁剪得到的四边形MNPE面积最大,请给出裁剪方案,并说明理由.

改编2
评注本题与原题相比,仅去掉第一问,即不对建模方式作任何暗示,给学生更广阔的探索空间.同时与改编题1比较,本题的最值不是在特殊位置取得,通过简单的实验操作不能解决问题,必须建立函数模型.试题背景相同,但解决方式不同,为学生创设更丰富的建模机会.
3.2 深刻理解情境,初定建模方案
数学应用问题是一个完整的知识结构系统,是用一定的情节描述的数量关系问题.情节和数量关系是它的两个基本构成要素, 两者密不可分.要让学生深刻理解应用题的情境及描述的情节,我们需要让学生置身情境,或操作,或联想.对于题2,我们尝试如下的研究方案:
研究方案1:实验操作,在动态观察中解决问题.对于改编1,最好的方式就是通过折纸进行操作,观察分析可知,四边形MNPE的面积一直在增大,实际上是建立了一种单调函数模型;

3.3 多法解模验模,探求最优解法
以∠EFD=θ或BE=t为变量建立目标函数求解,常见的解答方法如下:



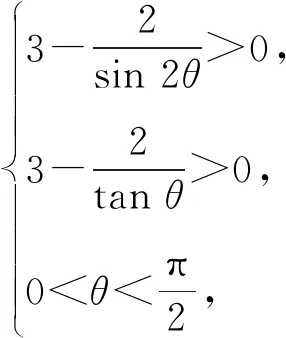

所以四边形MNPE面积为

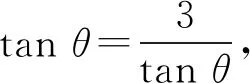
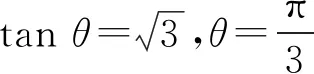
此时,(*)成立.
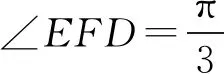
解法二:同解法一得

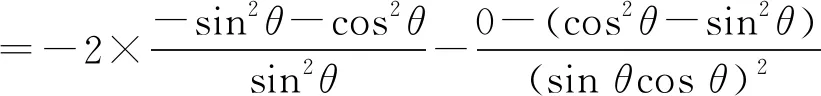


θ0, π3 π3π3, π2 S'θ +0-Sθ 增函数极大值减函数

解法三:设BE=t,3 因为∠EFP=∠EFD=∠FEP, NP=3-PF=3-PE=3-(t-BP) 所以四边形MNPE面积为 此时,(**)成立. 题2的解决过程是一次充分的、 深刻的建模解应用题的过程,是一次体验丰富的活动经验的积累过程.在解完题2后,我们要引导学生思考以下问题:通过本题的解决,你认为我们应如何合理地利用情境帮助数学建模?在本题中,关键的量有哪些,它们有什么关系?建立函数模型应如何结合关键的量进行设元?解题过程中需要考虑哪些限制条件?你还碰到过类似问题吗,它们有什么共同点和不同点?经常反思以上问题,帮助学生养成自我评估反思的习惯,实现自我监控,积累活动经验.




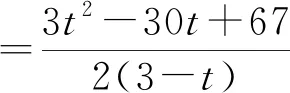



3.4 自我评估反思,积累活动经验

