三角形一个性质在四面体中的推广*
曾建国
(赣南师范大学数学与计算机科学学院 341000)
1 引言
众所周知,三角形的葛尔刚(Gergonne)点是指图1中三线之交点,即有

图1
命题1[1]连结三角形的顶点和内切圆与对边切点的直线,三线交于一点.
笔者在文[2]中将三角形的葛尔刚点的性质推广至四面体中,即有
定理1[2]若四面体有棱切球,则过每一条侧棱及棱切球与其对棱切点的平面,6个平面交于一点.
三角形还有另一个性质(参见图2、图3)

图2
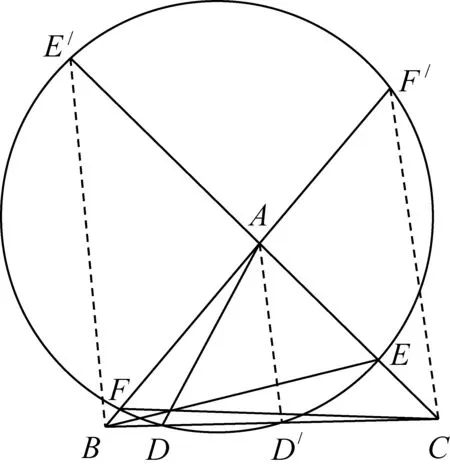
图3
命题2[3]一圆交△ABC的各边或其延长线于两点,设直线BC、CA、AB上的交点分别是D与D′,E与E′,F与F′,若AD、BE、CF三线共点,则AD′、BE′、CF′三线共点或平行.
笔者注意到,命题1与命题2有密切的联系:命题2中当圆与△ABC各边上两个交点重合为一点(即图2、3中的圆变成△ABC的内切圆)时,结论就变成命题1.因此,命题1是命题2的特例,命题2可以看作命题1的一种推广.
既然命题1可以推广至四面体中(定理1),那么命题2是否也可以推广至四面体中?本文试图研究此问题.
2 命题2的推广
将命题2推广至四面体中,有
定理2在四面体A1A2A3A4中,设侧棱AiAj(或其延长线)与一球面交于两点Bij,Bij′(1≤i 依题设知,平面A1A2B34、A1A3B24、A1A4B23有两个公共点A1和M,所以此三平面交于直线A1M.依题设又知A1M与侧面A2A3A4必交于一点M1,则直线A2B34、A3B24、A4B23交于一点M1. (1)当A2B34′、A3B24′、A4B23′交于一点N1时,因N1∈侧面A2A3A4,则直线A1N1与侧面A2A3A4相交于N1(见图4); 图4 图5 综合(1)(2)知: 同理可证: 当A1N1与A2N2均与所对侧面相交时(参见图4),A1N1与A2N2不平行是显然的; 综上可知,A1N1与A2N2共面但不平行,故可设A1N1与A2N2相交于点M′. 在定理2中,当球面与四面体每条棱上的两交点重合,即当四面体有棱切球时,就得到定理1的结论.因此,定理2可看作定理1的一种推广. 细心的读者可能会发现,定理2对点M的位置进行了限制,这是为了确保直线AmM(m=1,2,3,4)与顶点Am所对侧面均相交,从而便于在证明过程中能应用命题2的结论.至于M在其他特殊位置时情况较为复杂,有待进一步研究.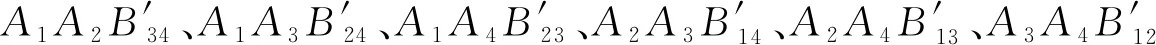
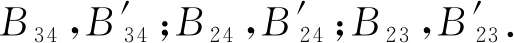
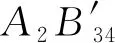


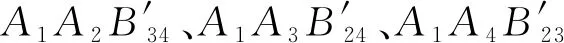



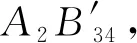
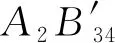
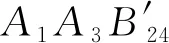

3 结语

