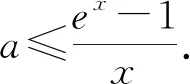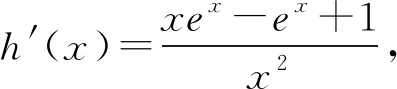回归概念是良策 洛氏法则为哪般

叶琪飞

(浙江省宁波市鄞州高级中学 315104)

本世纪以来，数学课程改革与教学方式的变革在中国大陆地区理性有序推进，数学教育界的有识之士，提出许多源于实践的教学建议，如，高考复习，回归课本、回归基础才是正道．回归有两层意思，一是学生能熟练运用课本知识解决“基础题”；二是养成从基本概念出发思考和解决问题的习惯．解题教学中，要使学生逐步养成从基本概念、基本原理及其联系性出发思考和解决问题的习惯，这是发展学生思维能力的正道．

遗憾的是，时至今日，仍然有些人在解题中过于渲染解题技巧，至于技巧怎么来的，其中又蕴涵着怎样的数学思想方法，常常不作解释，或语焉不详，让人感觉到如同“魔术师帽子里的兔子”般神奇．有些杂志也为此推波助澜，大量刊载解题技巧方面的文章．“洛必达法则”[5]-[10]就是追求技巧的一个典型例证，大有愈演愈烈之势．

笔者认为，“洛比达法则”确有它的方便之处，否则，在高等数学中就没有必要学习它了．现在的问题是，让高中学生学习“洛比达法则”是否合适？知道“洛必达法则”的学生(包括一些老师)是否是真正学习过它，理解它所蕴含的思想方法？还是仅仅知道它的操作步骤而已？就是对于教育发达地区的学生，如果是真正学习洛必达法则，也需要花费大量课时铺垫数学分析中很多有关内容，才可以使“洛比达”闪亮登场．即便如此，仍然冒学生只会机械模仿而不清楚其中道理的风险，学生很可能就把它仅当成一种解题技巧而加以记忆．这种夸大技巧掩盖问题本质的做法，往往会削弱真正的思想和方法，与数学核心素养的期许更是格格不入．事实上“数学是玩概念的，不是玩技巧的．技巧不足道也！”．

高中数学人教A版选修2-2第一章在用大量的篇幅介绍了导数的实际背景以后，抽象出了导数的概念的形式化定义：

它的等价形式是

这不仅说明“导数”是一种“特殊的极限”，而且还可以反向使用：为求某种特殊的极限也可以利用与之有关函数的导数给出．

下面通过几个具体的例子(全部改编于近几年的高考试题)介绍导数概念的这类应用，仅供有兴趣的师生参考，敬请指正！

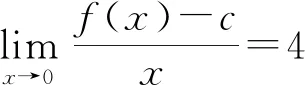
在暂时没有好的办法情况下，不妨将f(x)的表达式代入试一试，由此得到

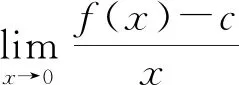
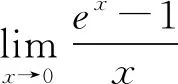
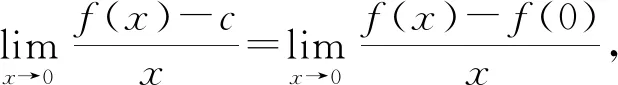
例2(2017，全国Ⅱ，文21)设函数f(x)=(1-x2)ex．

(1)略；

(2)当x≥0时，f(x)≤ax+1，求a的取值范围.

解析解决本题一般有两种方法，一是构造函数：g(x)=ax+1-f(x)，借助导数求出函数g(x)的最小值(如果存在的话)，令其非负，即可建立关于a的不等式，由此不等式可确定参数a的取值范围；二是利用所谓的“分离参数法”，这也是一般学生比较常用的一种方法．即

当x=0时，f(x)≤ax+1恒成立，此时a取值范围为R；

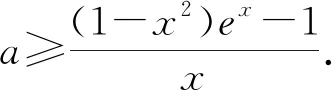
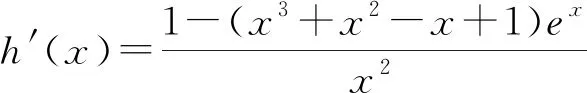
我们认为，此时是引导学生回到教材中去、回到导数的概念中去思考问题、解决问题的极好机会．

本题貌似不等式问题，实际上仍然以导数为工具研究函数最值问题．解题最后一步中充分发挥了导数概念的作用，值得细细品味．另外，解题过程中虽然两次求导，但它不同于高等数学里的“高阶导数”，它不过是一个基本想法的多次使用而已，即如果想知道一个函数是增函数还是减函数，那么看看它的导数是正的还是负的就可以了．

例3(2017，全国Ⅱ，理21)已知函数f(x)=ax2-ax-xlnx，且f(x)≥0．

(1)求a的值；

(2)略．

解析(1)文献[5][7]提供了分离参数后利用“洛必达法则”求一个特殊极限的方法，本文介绍利用导数概念求这个特殊极限的一种方法．

显然f(x)的定义域为(0，+∞)．

f(x)=ax2-ax-xlnx=x(ax-a-lnx)≥0

⟺g(x)=ax-a-lnx≥0⟺a(x-1)≥lnx．

(※)

当x=1时，(※)式恒成立，a取值范围为R；

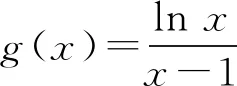
即当x>1时，a≥1．

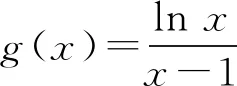
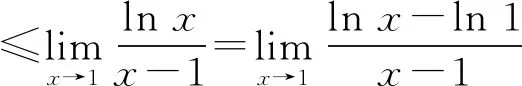
即当0

综上，a=1．

虽然高考试题里经常会出现以某些高等数学思想为背景设计的创新试题，但并不希望同学们用高等数学知识和思想方法来解答，这既不现实，也没有必要．

通过海外酒业市场调查，发现美国、澳大利亚、欧州消费市场、消费人群、消费喜好的消费特征，显示出中国白酒走出国门时的问题：如中外饮食习惯、文化差异导致了壁垒；国内外在对待酒类商品的贸易政策、行业标准上的不对等，对中国白酒的普及和国际化造成一定的限制；白酒价格与消费者购买力的不匹配等。因此，本文借助智猪博弈理论，论证出行业引领者的角色应当由政府或行业协会扮演，从国家级、省级层面去共同打开海外白酒市场。同时，依托中国白酒产业“品牌伞”，打好中国白酒的“文化牌”和“标准牌”，将有助于进一步提高中国白酒的国际竞争力与影响力，加速中国白酒国际化进程。

例4(2010，海南、宁夏，文21)设函数f(x)=x(ex-1)-ax2．

(1)略；

(2)若当x≥0时，f(x)≥0，求a的取值范围.

文献[8]对本题的评注是：第(2)还可以用分离参数法，但分离参数法需要用洛必达法则求极限，不可取．

认识到“用洛必达法则求极限，不可取．”是值得肯定的，但分离参数后却并不需要用洛必达法则求极限，只需根据导数的概念即可轻松求得a的取值范围，何乐而不为呢？

解析因为当x≥0，所以f(x)≥0等价于g(x)=ex-1-ax≥0．

当x=0时，g(x)≥0恒成立，

此时a取值范围为R；

而(xex-ex+1)′=xex>0，

所以当x>0时，xex-ex+1>0．

所以当x>0时，h′(x)>0，

即h(x)是区间(0，+∞)上的增函数．

所以当x>0时，

即a的取值范围为(-∞，1]．

通过多次使用导数的正负与函数的单调性的关系，最后遇到了一个“不定型”极限问题，突破这一难点的关键是仍然利用导数的概念，这一思维方式值得认真回味！可谓是非不能也，是不为也！

我们都认同“双基”教学的重要性，但是怎样才是真正的注重基础？对此，章建跃老师曾指出“注重基础”应该做到如下2个方面：

1．引导学生不断回到概念中去，使他们养成从基本概念出发思考问题、解决问题的习惯；

2．要加强概念联系性的教学，从概念的联系中寻找解决问题的新思路——解题的灵活性并不来自于“题型+技巧”，而是来自于概念联系通道的顺畅．

本文几个例题的解决又一次佐证了，数学概念是数学应用的“根”和“本”，根深才能长成参天大树，本固才能立于不败之地．解题教学应当追求解决问题的根本大法，也就是要引导学生在理解基本概念及其所蕴涵的思想方法上下功夫，将概念中蕴含的数学家思维打开，并用于训练学生，这是提高学生数学能力的捷径，也是提高高考成绩的法宝．

最后，我们必须指出，上述几例绝非仅有本文所介绍的这种解法，它们还有更自然、更简单的解法，我们的分析只是针对那些应用“洛必达法则”解这类题目的观点有感而发．不当之处，敬请谅解.

本文的撰写得到了特级教师王芝平老师的大力帮助，在此致以深切的谢意．