提升课堂问题思维价值的策略初探*——从两次县高中数学主题教研活动中获得的启示

王克亮

(江苏省射阳县教育局教研室 224300)

有效的数学教学离不开问题这一载体，没有问题就谈不上真正的数学教学，没有好的问题就不会出现精彩的数学课堂. 为了透视当前高中数学课堂老师们所设计的问题存在着哪些不足，并寻找其优化与改进的策略，近期我县举行了两次这样的主题教研活动，依托“等差数列”和“圆与圆的位置关系”这两节内容分别开设了6节观摩课，以下是我们的一些研讨纪要与共识.

1 当前课堂问题存在的一些不足

1.1 碎问

有些课堂问题接二连三出现，偏多偏碎，学生被动跟着老师走，思维没有机会深入，学生的主体地位不能得到充分凸显，问题的思维价值有点缺失.

案例1圆与圆的位置关系

在这节课上，就两个圆有哪几种位置关系，有的老师设置了如下一些问题：

问题1圆与圆的位置关系有哪几种？

问题2圆与圆的位置关系与它们的公共点个数之间有何关系？

问题3两圆的位置关系与它们的圆心距及两个半径之间有何关系？

问题4两圆公切线的条数与它们的位置关系之间有何关系？

问题5两圆相切时，切点与两个圆心的位置有何特殊性？

问题6两圆相交时，公共弦所在直线与两圆心的连线的位置关系如何？

评注这里的6个问题都限于讨论两个圆的位置关系及其特征，不少问题比较接近，思维的跨度与发散度不大，显得有些多而碎.

1.2 浅问

有些课堂问题简单浅显，学生一看便知，或者学生不需要作深入思考即可得到答案. 可有时这恰恰又是本节课的一个重要内容，不得不为之专门设置一个问题.

案例2等差数列

对于等差数列概念的给出，在6节观摩课上，老师们都是这样处理的：即先列举几个实例，然后提出一个问题，引导学生从多个实例中抽象出等差数列的概念，如：

(1)第23届到第28届奥运会举行的年份依次为

1984，1988，1992，1996，2000，2004.

(2)一堆钢管共5层，最下面一层是5根，上面一层总比下面一层少1根，则从下往上数，每层的根数分别为

5，4，3，2，1.

(3)某电信公司的一种计费标准是：通话时间不超过3分钟，收话费0.2元，以后每分钟收话费0.1元，则通话费按从小到大的次序依次为

0.2，0.2+0.1，0.2+0.1×2，0.2+0.1×3，….

(4)如果1年期储蓄的月利率为1.65‰，那么将10 000元分别存1个月，2个月，3个月，……，12个月，所得的本利和依次为

10 000+16.5，10 000+16.5×2，10 000+16.5×3，…，10 000+16.5×12.

问题上面这些数列有什么共同的特点？

评注该问题是苏教版教材中提供的范问，有较好的启发性与过渡作用. 但该问只涉及到特征观察与简单抽象，尚未涉及到深层次的思维，因而相对比较浅显. 教学中如果仅问于此，似乎还没有发挥其应有的价值.

1.3 浮问

有些课堂问题本身并不缺少思考与探究的价值，但在具体教学中，老师只是作一般性的处理就结束了，浮光掠影，未能将问题继续引向深入.

案例3圆与圆的位置关系

在本节课上，明确了两个圆具有哪几种位置关系之后，接下来的任务就是借助解析几何的方法来判断两个圆的位置关系了，这是本节课的核心内容. 在6节观摩课上，老师们都提出了如下问题或类似问题：

问题如何判断两个圆的位置关系？试以下面的两题为例进行探究.

(1)(x+2)2+(y-2)2=1与(x-2)2+(y-5)2=16；

(2)x2+y2+6x-7=0与x2+y2+6y-27=0.

对此，学生容易想到的方法是“判断圆心距d与两圆半径R,r之间的关系”. 在一些观摩课上，当学生回答出这样的方法之后，老师引导学生作了一般化就过去了.

评注解析几何中处理与圆相关的问题通常有两类方法，即几何法与代数法. 因为圆的特殊性，在运算上通常是几何法更为简便，所以很多老师习惯上只重视几何法的教学，对代数法往往只是提及，或者就略去不讲. 事实上，代数方法更能体现解析几何的本质，可为后面进一步学习圆锥曲线打下伏笔，所以上述处理方法欠妥，未能将问题推向高潮，留下了一些遗憾.

1.4 缺问

有些课堂，教者有明确的问题意识，也能用问题贯穿整个课堂，但在一些需要升华的地方却缺少问题的支撑，留下了遗憾.

案例4等差数列

在苏教版教材中，等差数列的通项公式是本大节中第2小节的内容，所以按教材的编写意图，在等差数列第1课时的教学中不一定要进行通项公式的教学.

但在6节观摩课中，有5位老师讲了通项公式的推导方法及公式的应用，或许这些老师认为，第1小节的内容较少且较简单，没有什么嚼头，只有讲解等差数列的通项公式才能上出精彩来.

评注事实上，所有与会老师都认为，剩下的没有讲解第2小节内容的那节课反而是最精彩的. 对比之后我们发现，上述5节课留有遗憾的原因是他们在一些可提升的点上没有置问，未能对相关知识进行及时升华.

2 提升问题思维价值的策略初探

2.1 多问融成一问

优化碎问的策略是对一些零碎问题进行恰当整合，尽量把多个性质相同或相近的问题融合成一个大问题. 问题变少变整了，其提示的因素就减少了，自然可发散学生的思维. 当然，对一些问题进行融合也是需要技巧的，要将它们的共同属性抽出来.

案例5案例1的改进

因为案例1中的6个问题都是关于两个圆的位置关系及其几何特性的，所以可将其融合为下面的一个问题：

问题两个圆的位置关系有哪几种？它们分别有哪些特性？

评注问题的前一半是按教学目标而设定的，它起到了回顾作用，因为初中已讨论过两个圆的位置关系；问题的后一半融合了案例1中的问题2～问题6，因为它没有给学生指明回答的方向，所以在探究过程中学生可能会从多个角度来思考这个问题，甚至还可能出现上述几个问题中没有涉及到的几何性质，这样就大大提高了问题的思维含量.

2.2 合理添加缀问

优化浅问的策略自然是加深问题的难度，但如果某个浅问是经典的，不便轻易改动，那么不妨在其后缀上一问，以提升思维含量. 当然，缀上什么样的问题是需要教者好好设计的，既要保证问题前后的和谐性，又要能引发学生的思考与探究.

案例6案例2的改进

在列举案例2中同样几个实例的基础上，可提出如下问题：

问题上述数列有何共同特点？如何表示出这样的特点？

评注因为前一半问题是教材提供的范问，而且它又具有很好的引导作用，所以教学中应该坚持使用. 当缀上 “如何表示出这样的特点？”这个问题之后，就能给学生创设一定的思考空间与探究空间，因为至少有以下几种方法可表示出这样的特点：

(1)文字表示法：从第二项起，每一项与前一项的差为常数. 这种表示方法可自然引出等差数列的定义.

(2)符号表示法：当n∈N*时，an+1-an=d(常数)；或者当n∈N*且n≥2时，an-an-1=d(常数). 这种表示方法是等差数列定义的数学符号语言直译形式，是证明一个数列为等差数列最直接的依据.

(3)连等表示法：当n∈N*时，an+1-an=an+2-an+1. 这种表示方法是等差数列定义的等价表示形式，是证明一个数列为等差数列的又一依据.

2.3 适时进行追问

既然浮问是对问题的处理不够深入，蜻蜓点水，未能将问题的价值尽可能地发挥出来，因而其优化的策略是在解决问题的过程中适时地加以追问，在不断的追问中将问题的价值尽可能地释放出来.

案例7案例3的优化

在学生给出了解决问题的几何方法之后，老师可作如下追问：

追问1类比直线与圆的位置关系的处理方法，还有其它想法吗？

对于第(1)小题，可得Δ=0，即两圆有且只有一个公共点，相切是肯定的，但还不能判定是外切还是内切；类似的，当Δ<0时，两圆无公共点，但还不能判断是外离还是内含，即这两种情况下位置关系的判定还要结合图形的具体情况. 对于第(2)小题，因为Δ>0，两圆有两个不同的交点，可断定两圆是相交的.

所以，代数法是可行的，但对于有些位置关系来说还要结合其它手段来判断.

课堂上，如果仅提到这样的代数法就结束了，还是有点遗憾，此时，我们可以作如下进一步的追问：

追问2对于第(1)小题，两圆方程相减，所得结果是一条直线，无论其代回到哪一个圆的方程中，结果都是相切的，说明该直线有什么样的特殊性？

意图引导学生发现这条直线就是两圆的公切线，在此基础上，可再作如下追问：

追问3在第(2)小题中，两圆方程相减所得直线方程无论代回到哪个圆的方程中，所得结果都是相交的，此时你有什么样的猜想？如何验证你的猜想？

意图引导学生猜想这条直线是两个圆的公共弦所在直线，并通过设出两圆交点坐标的方法来验证.

评注这里通过三次适时的追问，不仅介绍了代数法，完善了方法体系，体现了解析几何的本质，还顺利地过渡到了后面常用的结论中，可借机处理一下教材中的类似问题(如练习5，此略).

3 升华可处置问

改进缺问的策略自然是补上重要一问，即当课堂进行到可以对相关内容进行合理升华的时候，老师要及时置问，将研讨引向更高境界. 当然，在什么地方升华与置问，还是需要教者在课前备课时认真研究与设计的.

案例8案例4的优化

在等差数列的定义介绍之后，可从其定义的符号语言出发提出如下问题：

问题1你能判断下列数列是否为等差数列吗？你从中发现了什么？

(1)an=0； (2)an=n2； (3)an=-2n+4； (4)an=3n+1.

意图问题的前一半是想让学生运用等差数列定义的符号语言来判断所给数列是否为等差数列；问题的后一半是想借机作一个升华，引导学生猜想出“an=pn+q(p,q为常数)的数列一定是等差数列”这个结论.

为了给下节课作铺垫，这里还可以顺势介绍如下结论：

事实上，反之也是成立的，即等差数列的通项公式一定也是an=pn+q(p,q为常数)型的，所以其图象是一群弧立且共线的点. 下节课我们将要学习这个内容，这里先了解一下.

另外，在课堂的总结阶段也有升华的契机，可提出如下问题：

问题2通过本节课的学习，请总结一下，判断等差数列的常用方法有哪些？

意图将本节课的前后内容串联起来，明确判断等差数列的三类常用方法：

(1)定义型方法：即验证an+1-an(n∈N*)或an-an-1(n∈N*且n≥2)是否为常数(与n无关的数).

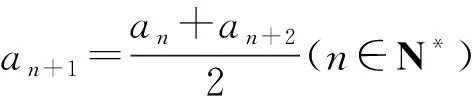
(3)特征型方法：即看其通项公式是否为an=pn+q(p,q为常数)型；或其图象是否为直线型；(将来还可以看其前n项和是否为Sn=An2+Bn(A,B为常数)型).

总之，碎问、浅问、浮问、缺问这些存在不足及其改进的策略仅是笔者对当前高中数学课堂问题的肤浅认识，更多存在不足的发现还有待于我们作进一步的观察与探讨，其优化的策略还有待于我们不断地进行思考与实践.