“先猜后证”是解决存在性探究问题的有效途径*

邱宗如

(福建省厦门市海沧区教师进修学校 361026)

所谓“存在性探究问题”就是探索满足确定条件的某一数学对象(如点、数值等)是否存在．“存在”就是有满足确定条件的数学对象，此时需要求出它们来；“不存在”则需说明理由．

由于存在性探究问题中的结论成立与否对问题的解决有直接的影响，所以如果事先能够探明“结论”就显得至关重要了．我们知道，“对普遍情况适用的对其中的特殊情况也必能适用；这是逻辑方面的常识．…从特殊到普遍，是我们获得知识的最基本的途径”．[1]所以解决存在性探究问题的一种有效策略是“先猜后证”．即从满足条件的特殊情形入手，若找到这个可能的数学对象，则再通过逻辑推理给出一般的肯定性证明；否则，可借助反例予以证伪．

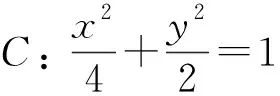
解析如果这个点Q存在，它的坐标可能是什么？因为事物的一般性寓于特殊性之中，并通过特殊性表现出来，没有特殊性就没有一般性．所以通过特殊化可以找到这个可能的点．

如图1，因为此时|PA|=|PB|，所以应该有|QA|=|QB|，

图1

即点Q在线段AB的垂直平分线上，亦即此时点Q在y轴上．

所以可设这个点的坐标为Q(0，y0)．

但是y轴上的点有无穷多个，点Q到底是哪个定点?

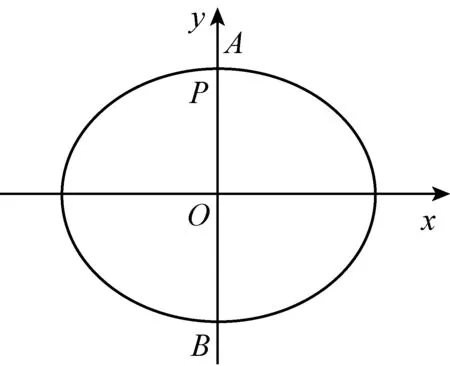
图2

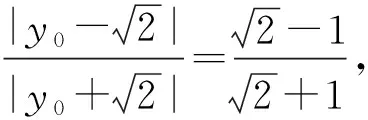
解得y0=1或y0=2．

所以不同于点P的定点Q的坐标只能为(0，2)．

这实际上是得到了结论成立的一个必要条件！

即如果满足题目要求的点Q存在，它只能是(0，2)！

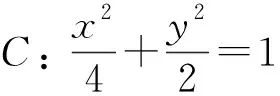
当l与两条坐标轴都不垂直时，怎样证明点Q(0，2)符合要求呢？

如图3，注意到线段PA与QA在x轴上的投影重合，线段PB与QB在x轴上的投影也重合，所以可分别作AC⊥y轴于C，BD⊥y轴于D．

图3

观察图形，不难发现Rt△ACP∽Rt△BDP，

只需证明Rt△ACQ∽Rt△BDQ即可．

证明当l与两条坐标轴分别垂直时，由上可知，结论成立．

当直线l与x轴不垂直时，设其方程为y=kx+1．

易知Δ>0，设A(x1，y1)，B(x2，y2)，

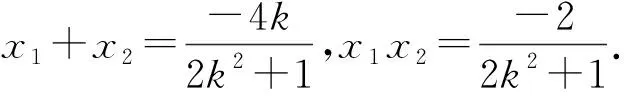
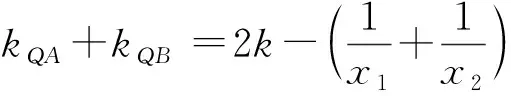
所以∠AQC=∠BQD，所以Rt△ACQ∽Rt△BDQ．

又Rt△ACP∽Rt△BDP，

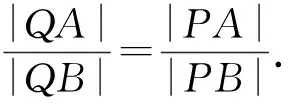
本题的解决是首先假设这个点Q存在，其次是通过一种特殊情形猜测出这个可能点在y轴上，“变大海捞针为池塘捉鱼”；再借助另一种特殊情形得到点Q的坐标，将目标集中于一点Q(0，2)．在验证一般情形结论也成立的过程中，充分发挥了几何图形的直观作用，比较容易地发现了证明的关键环节，即两组直角三角形的相似．借助几何直观可以发现、描述研究的问题，把复杂的数学问题变得简明、形象，有助于探索解决问题的思路、预测结果．

解析如果不知道这个常数λ是否存在，以及存在时λ等于多少，那么直接求解不但几乎不可能，甚至连求解的方向都找不到．反之，如果我们能预先把常数λ的值确定下来，无疑对寻找证明是有利的，那么如何确定λ的值呢？若我们确信这个常数是存在的，就应该从特殊情形入手，找到这个可能的常数，并希望由此发现解题的可能思路．

假设存在常数λ(λ>0)，使得∠QF2A=λ∠QAF2恒成立．

则对于第一象限内双曲线C上的任意一点Q，∠QF2A=λ∠QAF2都应该成立，

特别地，当QF2⊥x轴时，∠QF2A=λ∠QAF2也成立．

如图4，此时点Q的坐标为(2a，3a)，又A(-a，0)，

所以直线AQ的斜率等于1，即∠QAF2=45°．

又∠QF2A=90°，所以∠QF2A=2∠QAF2．

于是，我们完全有理由猜想所求的常数λ如果存在，那么它一定等于2．

当然，这只是个猜想，正确与否还有待于从一般的角度予以证明，即验证．

图4

图5

证明当QF2⊥x轴时，∠QF2A=2∠QAF2．

如图5，当QF2不垂直于x轴时，设Q(s，t)(s>a，s≠2a)，

又F2(2a，0)，

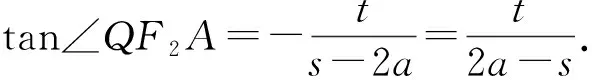
所以

所以tan∠QF2A=tan2∠QAF2，

即∠QF2A=2∠QAF2．

所以，存在常数2，使得∠QF2A=2∠QAF2恒成立．

“数学事实首先是被猜想然后是被证实．”(波利亚语)对于这个问题，我们先假设探究的数学对象λ存在(即结论成立)，执果索因，通过特殊情形猜想出λ的可能值，由此展开必要的逻辑推理．

在本文的两个存在性探究问题中，因为题设中并不知道这个定点或参数的值是否存在，以及如果存在它们是什么，所以求解会有一定的困难．通过特殊情形猜出这个定点的坐标或参数的值，则问题完全就变成验证了．而验证是有明确方向的，因此就简单得多．毕竟论证一个结论明确的数学命题比解决一个不明就里的数学命题要来得容易一些．

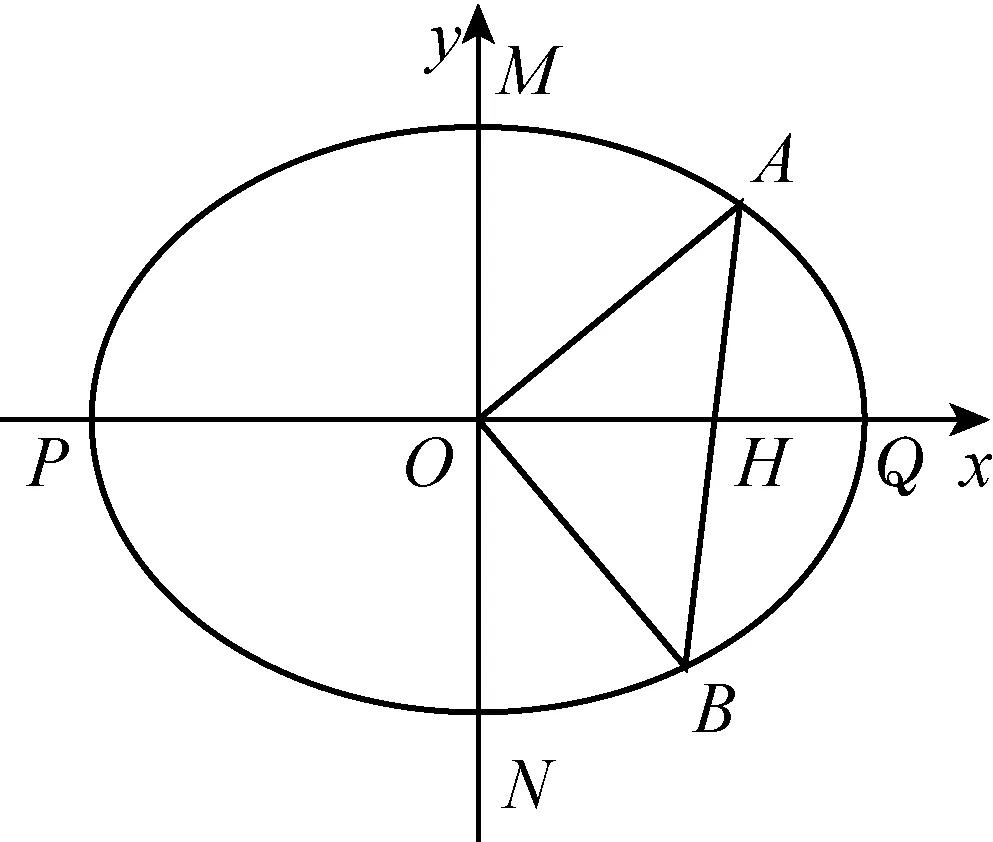
图6

如图6，设椭圆C与坐标轴分别交于P，Q，M，N，显然∠MOQ=∠NOP=90°，但是直线MQ与直线NP并没有公共点，即它们不过同一点．进而可知不存在满足条件的定点H．

对于存在性探究问题，如果通过两次不同的特殊情形得到不同的结论，那么可以肯定探究的数学对象就不存在，即通过反例证明结论是错误的．

但是，没有大胆的猜想，就没有伟大的发现．猜想数学命题和解题思路是数学研究中重要的思维过程．需要注意的是，任何一个有价值的“猜想”都不是空穴来风，它与无方向的乱猜，或者用掷骰子的方法碰运气是格格不入的．它需要对数学基础知识的精准理解和数学思想方法的灵活运用．几乎每一个复杂或困难问题的求解都会经历探索、尝试、猜想等过程，有时需要大胆地跳跃到某种结论上(即先有一个大致的方向)，然后，再去小心地求证．

本文表明，通过特殊化而获得一般性结论是猜想的有效途径之一．对此数学大师希尔伯特有精彩的论述：“在讨论数学问题时，我们相信特殊化比一般化起着更为重要的作用．可能在大多数场合，我们寻求一个问题的答案而未能成功的原因，是在于这样的事实，即有一些比手头的问题更简单、更容易的问题还没有完全解决或是完全没有解决．这时，一切都有赖于找出这些比较容易的问题并使用尽可能完善的方法和能够推广的概念来解决它们．”[3]

著名数学教育家乔治·波利亚对“猜想”亦非常重视，把它列为对数学教师的基本要求之一，他认为“在数学领域中，猜想是合理的，值得尊敬的”．他还向所有数学老师呼吁：“让我们教猜想吧！”[4]他语重心长地告诫我们，“先猜后证”是大多数情况下的发现过程．数学教师有极好的机会向学生说明猜想在发现过程中的作用，以此给学生奠定一种重要的思维方式．并希望数学教师在这方面不要忽略了对学生的要求：让他们学会猜想问题．

求解圆锥曲线存在性探究问题是教学生猜想的一个极好机会，有意识地进行“先猜后证”的思维训练，对于提高学生的解题能力，提升数学核心素养是极为有益的．