域椭圆曲线点乘的VLSI实现方法研究

李 超，张 强，曲英杰

(青岛科技大学 信息科学与技术学院， 山东 青岛 266061)

域椭圆曲线点乘的VLSI实现方法研究

李 超，张 强，曲英杰

(青岛科技大学 信息科学与技术学院， 山东 青岛 266061)

为了实现椭圆曲线密码算法的高效性，提出了基于优化的底层有限域算法的点乘设计方法;基于对二进制有限域运算的研究，提出并行模乘算法和基于欧几里得算法的右移求逆算法，并在实现中进行优化，在此基础上采用蒙哥马利算法实现点乘的快速运算；根据该算法，提出了ECC硬件电路实现方法，并用Verilog RTL进行逻辑设计，最终在Xilinx的XC7A100T FPGA硬件平台上验证实现;通过仿真测试、综合验证和时序后仿真的结果分析，所设计电路的时钟频率可以达到110 MHz,运算速度可达2.92 ms，证明了设计的有效性和可行性。

椭圆曲线密码；二进制域；点乘；模乘；模逆

0 引言

椭圆曲线密码算法(elliptic curve cryptography, ECC)因其密钥长度小、安全强度高、便于硬件实现等优点，广泛的被用于硬件实现的加密系统中[1]。其中，点乘运算是实现椭圆曲线密码高效性的前提条件，而有限域算术运算的有效实现则是点乘的关键[2]。目前广泛采用的GF(2m)点乘算法实现主要是分别设计底层的有限域运算单元，然后通过协处理器或者其他控制电路来调用底层其他各功能单元[3]。所以研究并有效实现域运算层的各个模块是研究基于FPGA的ECC点乘运算的关键。通过研究近年的实现方案，文献[4]采用Montgomery点乘算法实现并行调度分解，跳过点加和倍点的调用过程，解决了顶层调用复杂的问题，提高了顶层的运算速度，但其底层四路的调度缓慢且复杂，导致资源开销较大。文献[5]中对于底层域乘法运算的实现，虽然在运算过程中对算法进行了改进，在运算过程中同时完成了相乘和取模运算，节约了资源，但是却牺牲了运算速度和效率。考虑硬件电路实现的特点和优势，本文采用GF(2m)内的椭圆曲线作为硬件的实现方案，选用实现效率高的蒙哥马利点乘算法，通过设计并行的模乘算法和改进的模逆算法，实现点乘运算的电路结构设计，取得了良好效果。

1 椭圆曲线加密系统

二进制有限域GF(2m)上的Weierstrass方程如式(1)所示：

y2+xy=x3+ax2+b,a,b∈GF(2m),b≠0

(1)

当b=1时称为Koblitz曲线。此类曲线在椭圆曲线密码体制的实现中速度是最快的。椭圆曲线密码方案的安全性问题是基于椭圆曲线的离散对数问题(elliptic curve discrete logarithm problem, ECDLP)，这也是它优于包括RSA在内等公钥密码体制的原因。椭圆曲线离散对数问题是：给定有限域Fq和定义在其域上的椭圆曲线E(Fq)，若已知椭圆曲线上的点P，求Q=KP很容易，但是反过来，在已知P和Q，求K值就非常困难，这样就可以把Q看做为公钥，K为私钥[6]，这就是椭圆曲线的点乘原理。由于在ECC中，多项式f(x)为稀疏多项式，且多用三项式或者五项式，即f(x)的二进制表示仅仅只有3或者5位为1，其余值全为0。在后文的讨论中，本文采用的都是三项式基f(x)=x233+x74+1，即m=233。

2 有限域运算的电路结构设计

为了顺利实现点乘算法，本文将重点放在设计有限域运算模块上，该模块可以完成有限域上的加减法、模乘、模逆和除法运算。其中，二进制域的加减法器结构简单，可采用逐位异或的电路结构处理[7]，即用N个异或门实现，在时钟上升沿且复位电平无效时，在一个周期内即可完成m位数据的逐位异或，实现简单且速度较快，如图1所示。

图1 模加(减)异或门

2.1 模乘算法分析与改进

模乘运算是椭圆曲线点乘运算高效实现的关键，用域元素a,b∈GF(2m)分别表示多项式A(x) =am-1xm-1+... +a1x+a0和B(x) =bm-1xm-1+... +b1x+b0，则域元素a与b的乘积公式为：

P(x) =A(x)×B(x)bmodF(x) =

这里F(x)是域不可约多项式。

从乘积公式可以看出，模乘的过程包括相乘和取模两个过程。传统的乘法是将两个m位操作数相乘，然后对其进行f(x)求模。二进制域上的乘法实现有多种形式，主要有串行结构，并行结构，串并相结合的数位并行结构。为了提高模乘算法的效率，参照文献[7]中所介绍的典型移位串行算法，并对其进一步优化，其中文献[7]中的算法如下：

输入：A(x) =am-1xm-1+... +a1x+a0,B(x) =bm-1xm-1+... +b1x+b0，不为零的最高位为m的多项式f(x)。

输出：a(x)·b(x)modf(x)。

1)若a-1modf(x)=1,则有C=B，否则C=0；

2)i从1到n-1循环;

(1)b=(b<<1)modf(x) ;

(2) 若ai=1，则c=cmodb;

3)返回c。

该算法通过串行移位的方法，一个时钟进行一次移位的操作，然后进入下一步的异或运算，那么完成m位的运算则需要m个clock，所需时间较长。根据二进制模约减运算的特点，在求模运算中，其实上是判断被模数的最高位数值。最高位为1的话，就将被模数与f(x)进行异或处理；反之不变，保留原值。故可以考虑采用并行的思想，可以首先并行的得到(1)步骤中所有bi的值，然后采用并行的方式完成步骤(2)中的运算。改进算法描述如下：

输入：a,b∈GF(2m),a≠0,b≠0,约减多项式f(x)。

输出：c=a·bmodf(x)。

1)若a-1modf(x)=1,则有C=B，否则C=0；

2)i从1到n-1循环

(1)b=b<<1

若bm-1=1,则b=b⊕f(x)；

否则b=b；

(2)若ai=1，则c=c⊕b;

3)返回c。

根据移位方法并行获取bi的思想，如表1所示，考虑到最高位，即b(233)、bi(233)都为1，为了表示简洁，此处略过这项。

观察表1，232个233位的bi，只与b，bi(0)，bi(232)有关。

(1)对于bi(0)，有：

b(232)=1，则b1(0)=1；b(232)=0，则b1(0)=0;

b1(232)=1，则b2(0)=1；b(232)=0，则b2(0)=0;

类推;

bi(232)=1，则bi+1(0)=1；bi(232)=0，则bi+1(0)=0；

所以b1(0)～b158(0)仅与b(232)～b(75)有关，可以一次并行得到；对于b159(0)～b232(0)与b1(74)～b74(74)有关。由此，下面先讨论bi(74)的计算，然后再讨论b159(0)～b232(0)的求取。

表1 bi的求取过程

(2)对于bi(74)，有：

b(232)=1，则b1(74)=～b(73)；b(232)=0，则b1(74)=b(73);

b1(232)=1，则b2(74)=～b1(73)=～b(72)；b1(232)=0，则b2(74)=b1(73)=b(72);

类推：

当i<=74：

bi(232)=1，则bi(74)=～b(74-i)；bi(232)=0，则bi(74)=b(74-i);

当i>74：

bi(232)=1，则bi(74)=～bi-74+1(0)；bi(232)=0，则bi(74)=bi-74+1(0);

故b1(74)～b158(74)仅与b(232)～b(75)有关，可以一次并行得到；对于b159(0)～b232(0)以及b159(74)～b232(74),与b1(74)～b74(74)有关，而这74个值也只与b(232)～b(159)有关，可见bi表格中的数据全部依赖于输入b,，故可以一次全并行得到全部的bi值。然后将所有bi值进行存储，便于下面步骤中的异或操作，最终通过计算获得模乘的运算结果。

2.2 二进制域模逆算法分析与改进

模逆运算是有限域算术运算中最复杂，同时也是最耗时的，这里我们简单的用非零元素a来表示二进制多项式a(x)。在二进制域中，非零元素a的逆元素是域GF(2m)的唯一的一个元素g，在域GF(2m)上满足ag=1,即满足ag≡1(modf)。这个逆元素用符号a-1modf表示，也可直接表示为a(x)。目前广泛采用的主要有基于扩展的欧几里得算法和基于费马小定理的模逆算法来实现[8]。基于费马小定理的算法是将求逆运算换成模乘和模平方运算，算法评估完成模逆运算需要log2(m-1)+w(m-1)-1次模乘和m+1次模平方运算[9]，这样不仅会使软硬件的设计复杂度有所增加，同时在运算过程中由于反复调用模乘和模平方运算，性能也会因此大打折扣。而基于扩展的欧几里得算法因为在运算过程中只涉及到移位、判断和异或运算，并没有大量的乘法运算，所以比较容易硬件上的实现，可以方便的并行化设计。因此针对目前广泛采用的欧几里得算法[10]，进行进一步的改进，使其可以在运算过程中同时进行求逆和取模的运算。如此，在运算过程中同时进行移位判断的操作，所以输入为m位的求逆运算，最多只需2m个时钟周期就可以完成，从而大大提高运算效率。本文采用的模逆算法如下描述：

输入：次数不高于m的非零多项式a(x)、b(x)和既约多项式f(x)。

输出：a-1modf(x)。

1)u=a,v=f;

2)若mode=0,x1=1,若mode=1,x1=b;x2=0。

3)当u≠1和v≠1时，重复执行：

(1)当u是偶数时，重复执行：

u=u/2;

若x1是偶数，则x1=x1/2;

在水利工程施工中，机械的使用费约占产值的30%。水利行业特点决定了水利工程施工对机械设备有特殊要求：首先要求机械设备适应水利工程交通不便，受水文、气象、地形等因素的影响较大及大部分水利工程施工周期较短等特点；其次是要适应和满足水利工程项目自身的施工要求。

否则，x1=(x1⊕f)>>1;

(2)当v是偶数时，重复执行:

v=v/2;

若x2是偶数，则x2=x2/2;

否则，x2=(x2⊕f)>>1.

(3)当u≥v，则u=(u⊕v)>>1;

若x1和x2的奇偶性相同，则x1=(x1⊕x2)>>1;

否则，v=(v⊕u)>>1;

若x1和x2的奇偶性相同，则x2=(x1⊕x2)>>1;

若x1和x2的奇偶性不同，则x2=(x1⊕x2⊕f)>>1.

4)若u=1,则返回(x1)；否则，返回(x2)。

本算法中，添加一个mode模式控制位，当mode=1时，将初始条件变为x1=b;x2=0，便可以计算模除b/amodp，可以通过Euclidean传统算法证明验证。如此，通过mode的值选择即可完成模除或者模逆的运算，如步骤2所示：当mode=0时，进行模逆运算，mode=1时，进行模除的运算。通过将模除和模逆运算合并为一个运算，电路设计中就可以复用一套电路，再添加一些额外的条件判断电路和控制电路即可同时完成两种运算，节省大量的操作，从而达到节约资源，优化电路面积的效果。

3 椭圆曲线点乘的FPGA实现

采用Montgomery算法实现椭圆曲线点乘运算设计主要分为三个过程：1)预处理模块；2)循环运算模块；3)坐标转换模块。根据Montgomery算法特性[11]，在模块运算中并不涉及纵坐标y的计算，输入仿射坐标p(x,y)和二进制数(ki-1,...,k1,k0)2。

预处理模块主要完成数据的初始化工作，并为下一模块的输入提供数据，通过输入点P的仿射坐标(x,y)产生投影点P1(X1,Z1)，并调用一次倍点运算产生P2(X2,Z2)，以供循环模块使用。由于P1和P2相对应，因此投影点P1的横坐标初值为X1=x，Z1=1，投影点P2的横坐标是P1经过倍点运算得到。

在第二部分的主循环运算，是其中最耗时的模块，同时也是控制部分最复杂的设计模块。主要包括移位单元以及群运算层的点加和倍点运算，这也是点乘运算中最耗时的运算单元。当输入值k的二进制位ki=0时，(X1,Z1)作为倍点模块的输入，(X1,Z1)和(X2,Z2)作为点加模块的输入。

第三部分的坐标转换模块主要功能是在模逆运算完成后，将投影坐标再次转换为仿射坐标。由于在第一部分的预处理模块中，已经事先将点的仿射坐标转换为了投影坐标，所以在进行点加和倍点运算的时候就不需要再进行模逆运算，只需要在最后一次模逆运算完成后进行坐标的逆变换即可。

根据Montgomery算法特点，由于点加和倍点不存在数据相关性，可以并行调度点加和倍点，点加和倍点运算又同时调度有限域运算，因此可以将这个调度过程理解为点乘对有限域运算的调度。点乘完成一次迭代运算需要调用1次点加和1次倍点，主循环部分共需要完成m-1次迭代。在有限域调度中，用M表示模乘时间，I表示模逆时间，AS表示模加时间，在投影坐标下，一次点加调用需要时间6M+2AS，一次倍点调用6M+1AS。所以点乘运算的一次迭代共调用12次模乘运算和3次模加运算，采用并行调度后，完成一次迭代时间就相当于6个模乘时间(模加时间可忽略)。再加上最后坐标逆变换的一次模逆运算，所以完成一次点乘时间为6M*(m-1)+I。考虑到模乘、模逆实现所需要的时钟周期，所以一次点乘需要6m*(m-1)+2m个时钟周期。最终输出结果坐标即为标量乘法kP的坐标(X2,Z2)。

图2 基于蒙哥马利算法的椭圆曲线点乘运算的系统结构

在确定了标量乘的总体框架后，本设计的重点放在有限域的电路结构设计上。这个模块功能强大，根据本文提到的有限域算法，在控制器的作用下完成具体的电路运算。并且改进的求逆算法在判断条件上具有并行性，运算步骤可以流水处理，基于FPGA设计了高效的并行执行结构，在算术逻辑运算中主要由加法器、减法器、移位控制电路、异或电路、比较器和一些逻辑电路组成。实现的硬件结构如图3所示。

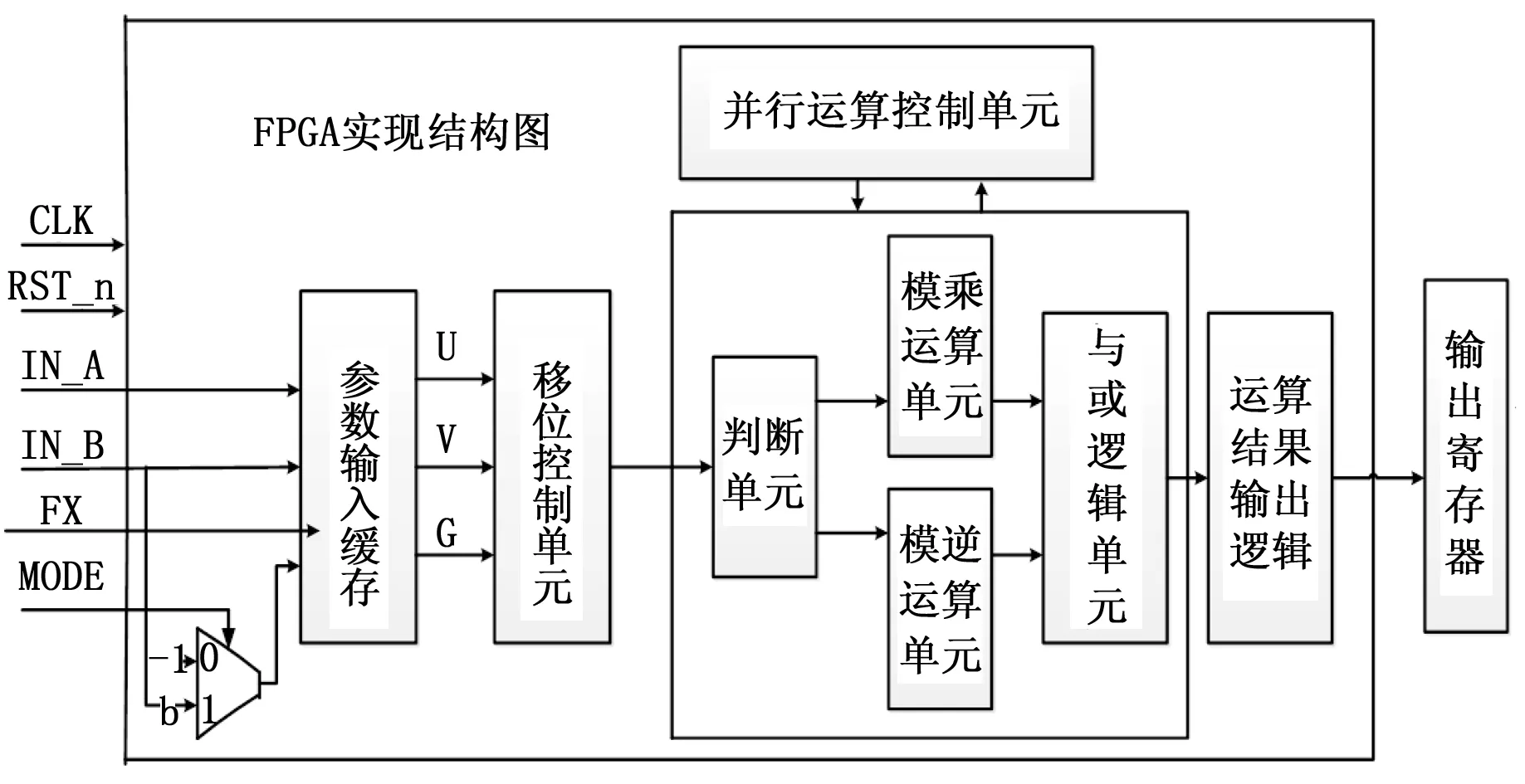
图3 有限域运算结构图

4 实验结果分析与性能比较

为了验证电路结构的正确性和有效性，同时为了与其它研究成果进行对比，选用创龙的开发板作为硬件验证平台进行点乘运算电路的FPGA原型验证，平台芯片为Xilinx的ARTIX 7芯片,型号为XC7A100T，封装为FGG484。使用Verilog硬件描述语言进行RTL级模型代码描述，并通过Xilinx公司的Vivado 2015开发软件进行编译综合、布局布线和时序分析。通过Mentor Graphics公司的modelsim10.1开发软件编写Testbench，输入测试激励进行了功能调试仿真。综合和布局布线之后，进行相应的时序约束，在满足电路内部寄存器的建立保持时间，没有时序违规的前提下，时钟频率最高可达110 Mhz，且输出结果完全正确。当m=233时，根据前文所得的时钟周期数，可以计算完成一次点乘运算时间为2.92 ms。同时，为了验证逻辑功能是否正确，时序是否符合要求，先单独对独立的有限域模块进行测试，所用参数是NIST推荐的GF(2m)域上长度为233的椭圆曲线。图4，图5分别是对模逆模块和标量乘模块进行的仿真测试结果。

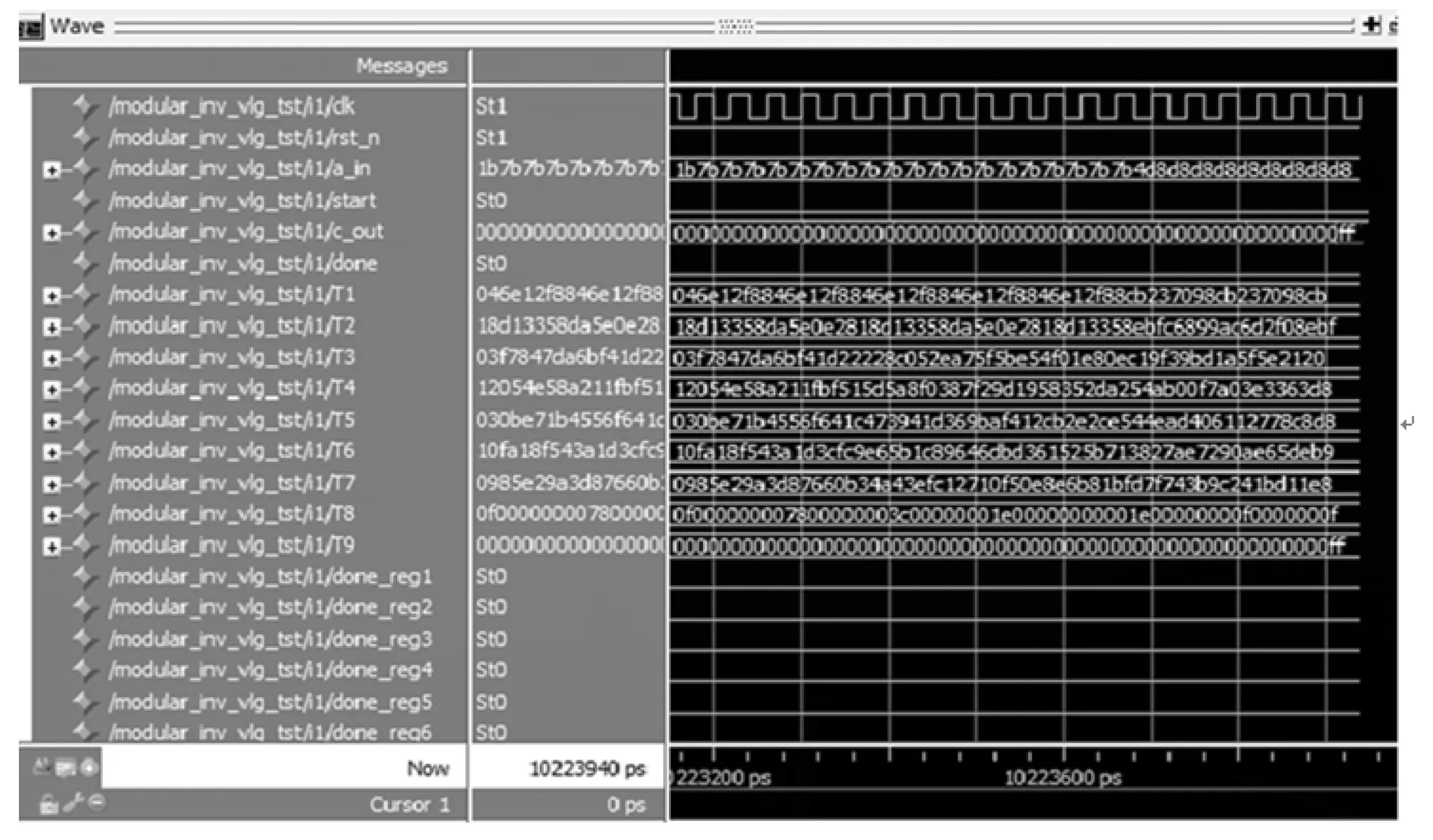
图4 二进制域模逆仿真波形图

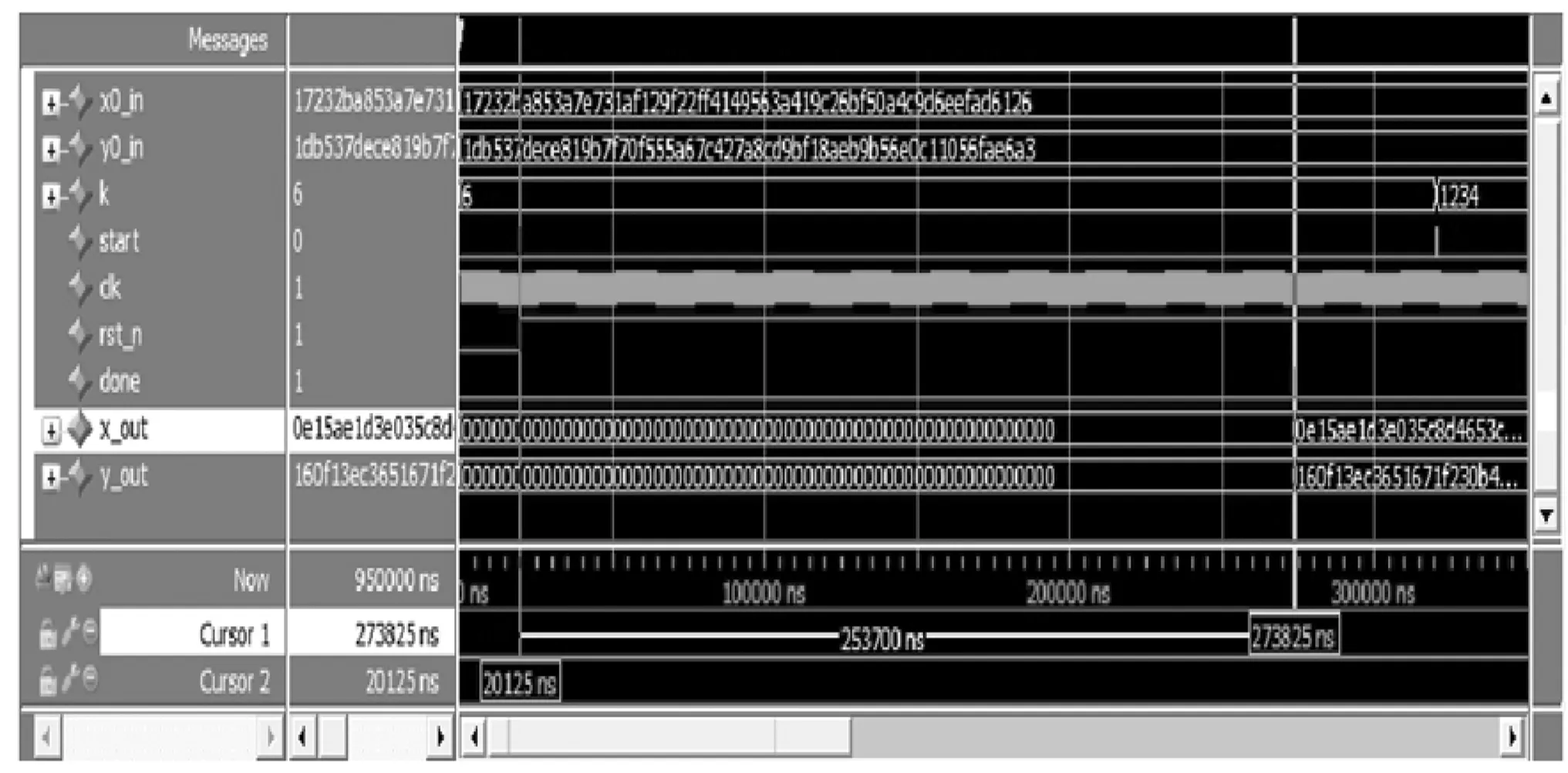
图5 二进制域标量乘仿真波形图

1)模逆仿真测试：向量输入a_in，模逆输出结果值 c_out。

a_in=233'h1b7b7b7b7b7b7b7b7b7b7b7b7b7b7b7b7b7b7b7

b4d8d8d8d8d8d8d8d8d8

c_out=233’ff

2)标量乘模块测试：向量输入k，x0_in和y0_in，点乘输出结果为x_out和y_out。

k=6；

x0_in=233’h17232ba853a7e731af129f22ff4149563a419c

26bf50a4c9d6eefad6126；

y0_in=233’h1db537dece819b7f70f555a67c427a8cd9bf18

aeb9b56e0c11056fae6a3；

x_out=233’h0e15_ae1d_3e03_5c8d_4c92_5391_63f2_3d13_243f_eb57_b45a_dbe4_cf7e_c619_57f6;

y_out=233’h160f_13ec_3651_671f_201b_b64d_ff8d_f25a_f3eb_c5c3_f9bf_c5cb_17b2_2037_03a8;

表2列出了本设计与近年其他一些文献研究的实验数据对比，主要包括完成一次点乘所需时间和逻辑资源的消耗情况。通过采用Synopsys公司的Design Compiler进行仿真后综合，查看系统设计的综合报告可以看出，本设计共用9302个LUT，大概4651个slice。通过查阅对比相关文献，虽然各文献所实现的硬件平台不一样，但是我们依然可以参考设计的运行时间、面积规模和域的不同来进行对比，分析电路的执行速度和逻辑资源消耗情况。文献[12]通过改进了模乘算法，面积上得到了优化，但是却牺牲了点乘的实现效率，在82M的时钟主频下，本设计的速度相对提升了54%。文献[13]采用了点乘的并行分解调度运算，但是未提出域运算层次的算法优化，虽然比本设计速度占优势，但是硬件资源消耗比本设计多了48%。相对于其他设计，本设计也取得了面积和速度的较好折中，资源消耗也有明显改善，经济性上更为突出。

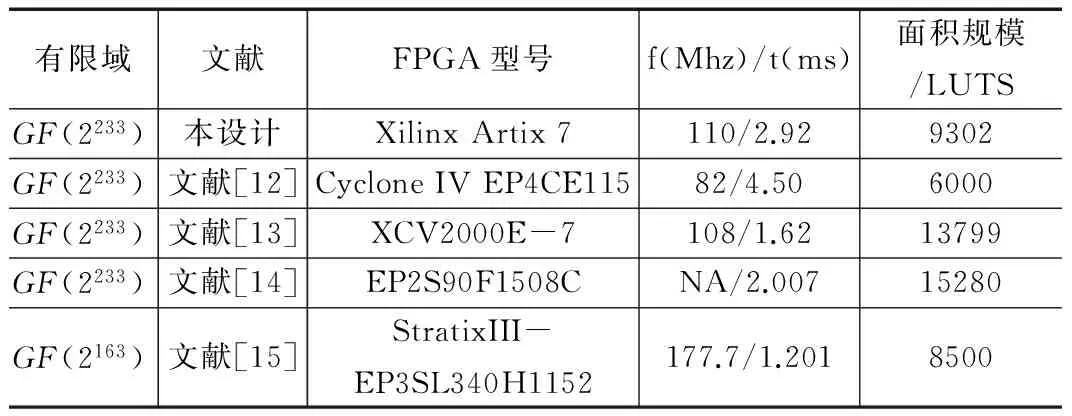
表2 FPGA设计速度比较

5 结束语

本文通过研究椭圆曲线有限域的算术运算，根据ECC的多项式的稀疏特点，提出并行的模乘思想，并改进传统的欧几里得右移求逆算法，使其可同时完成模逆和模除运算，以此为基础设计了有效的点乘电路并进行FPGA原型验证。实验结果表明，当数据位宽为233位时，只需2.92 ms即可完成标量乘运算。相较于其他算法，本设计大大提高了运算速度，资源消耗较少，取得了面积和速度的较好折中，在已公开的文献中性价比较高。尽管本文采用的模多项式是三项式基，但对于其他多项式基同样适用，同时只需修改电路设计输入的参数值即可实现其他不同位宽数据的要求，保证了设计的有效性、通用性和可研究性。

[1] 赖忠喜,陶东娅,张占军.GF(2n)域椭圆曲线密码体制中快速标量乘算法的研究[J].计算机应用与软件, 2014,31(8):324-326.

[2] 谢天艺. 素数域椭圆曲线密码SoC的设计与实现[D].杭州:浙江大学, 2015.

[3] 赖忠喜,张占军,陶东娅.椭圆曲线底层域快速算法的研究[J].计算机工程与应用,2014,50(3):67-70.

[4] 赖忠喜, 张占军. 椭圆曲线底层域快速算法的优化[J]. 计算机工程与应用, 2015, 51(22):115-118.

[5] 张莉华, 蔺 莉. 一种安全高效的椭圆曲线密码抗功耗攻击算法[J]. 测控技术, 2016, 35(8):118-121.

[6] 胡诗玮,徐和根.有限域GF(2～(256))上椭圆曲线密码算法的硬件设计[J].机电一体化, 2015,21(2):71-75.

[7] 郑建宏,周 亮. 椭圆曲线加密算法在卫星通信中的应用[J]. 信息通信,2016,31(02):209-210.

[8] 石亚娟, 黄辉辉, 陈建华. 基于智能卡的动态身份认证协议[J]. 电子技术应用, 2015, 41(3):97-100.

[9] 尹 恒. ECC标量乘算法在抗边信道攻击上的应用研究[D].贵阳:贵州大学,2015.

[10] 白永祥. 椭圆曲线密码算法在VPN安全握手中的应用[J]. 电子设计工程, 2015, 23(13):18-20.

[11] 郭高峰,崔强强.基于GF(2～m)的椭圆曲线求逆算法的改进研究[J].现代电子技术,2014,37(18):19-22.

[12] 操志辉.GF(2～m)域上ECC标量乘的设计与FPGA实现[D].武汉:武汉理工大学,2014.

[13] Urbano-Molano F A，Trujillo-Olaya V，Velasco-Medina J. Design of an elliptic curve crypto processor using optimal normal basis over GF( 2233) [A].2013 IEEE Fourth Latin American Symposium on Circuits and Systems( LASCAS)[C]. Cusco：IEEE，2013：1-4.

[14] 田 祎, 刘爱军, 申卫昌. 基于梳状算法的椭圆曲线密码标量乘改进方案[J]. 微电子学与计算机, 2015, 32(5):99-103.

[15] 王云峰，王 静，黄世伟．一种两路并行调度的点乘算法硬件实现[J]．新型工业化，2014，4(7)：20-27.

Research and Implementation of Point Multiplication Over Elliptic Curve F2mBased on VLSI

Li Chao，Zhang Qiang，Qu Yingjie

(School of Information Science & Technology, Qingdao University of Science and Technology, Qingdao 266061, China)

To realize the elliptic curve cryptography (ECC) effectively, the design method of modular multiplication based on optimized binary finite filed algorithm was presented. By the study of the binary finite fields, paralleled modular multiplication algorithm and inversion algorithm which was based on Euclidean algorithm were presented. The two algorithms were optimized during the process and then realized the fast evaluation of point multiplication by adopting Montgomery algorithm. ECC hardware implementation design was proposed based on the algorithm, and converted to logic designs using Verilog RTL, finally it worked on the XC7A100T FPGA platform of Xilinx. By pre-simulation, synthetical verification and analyzing the results of post simulation, the clock frequency of the designed circuit could reach up to 110MHz and the operating rate attained to 2.92 ms which demonstrated the feasibility and effectiveness of the project.

elliptic curve cryptography ; GF(2m); point multiplication; modular multiplication; modular inversion

2017-05-18；

2017-06-06。

山东省科技计划项目(2013YD01038)。

李 超(1990-)，男，山东枣庄人，硕士研究生，主要从事集成电路设计与嵌入式系统方向的研究。

曲英杰(1964-)，男，山东青岛人，博士，教授，硕士生导师，主要从事集成电路设计与数据加解密方向的研究。

1671-4598(2017)12-0232-05

10.16526/j.cnki.11-4762/tp.2017.12.060

TN918

A