善用数学模型，秒解中考试题

舒盛花

[摘  要] 随着课改的深入，数学更注重抽象思维能力的培养，更贴近解决生活中的实际问题. 平移模型，“K”形模型，将军饮马模型等是初中数学解题教学的常见模型，这类数学问题对能力要求较高，需要教师引导学生将所学内容整理归纳出类型和方法，并经过加工提炼和保存.

[关键词] 数学模型;平移模型;K形模型;将军饮马模型

平移模型、“K”形模型、将军饮马模型是中考的热点，这类问题既充满生活的趣味性，又是对数学思维的挑战，对能力要求较高，需要灵活地运用图形特点抽象概括出解题方法，并加以应用和拓展，形成解题经验，我们把这些图形或数学问题称为数学模型. 在平时教学中，老师如果善于总结常见的数学模型，会给复习带来事半功倍的效果. 本文结合笔者平时的教学，谈谈在初三复习中如何善用数学模型，秒解中考试题.

平移模型

浙教版教材七年级下册1.5中我们学过了“图形的平移”，移动的特点是在移动过程中原图形上所有的点都沿着同一方向移动相等的距离. 利用这一特性，教学时可以把“图形的平移”转化为“点”的平移来解决类似平行四边形的问题.

例1 如图1，在平面直角坐标系中，已知点O（0，0），A（1，-1），B（4，0），点M为坐标平面内一点，若以点O，A，B，M为顶点的四边形是平行四边形，则点M的坐标是______.

分析  由O，A，B，M为顶点的四边形是平行四边形，可分2种情况.

解答  （1）以OA为一边，即OA∥BM，此时，①若点M在点B的下方，则O（0，0）平移到A（1，-1），可知横坐标增大1，纵坐标减小1，由平行四边形的性质（对边平行且相等）可知B（4，0）平移到点M，则其横坐标增大1，纵坐标减小1，故M₁（5，-1）;②若点M在点B的上方，则A（1，-1）平移到O（0，0），可知横坐标减小1，纵坐标增大1，由平行四边形的性质可知，B（4，0）平移到点M，则其横坐标减小1，纵坐标增大1，故M₂（3，1）.

（2）以OA为对角线，则OM∥BA，此时B（4，0）平移到A（1，-1），可知横坐标减小3，纵坐标减小1. 由平行四边形的性质可知，O（0，0）平移到点M，则横坐标减小3，纵坐标减小1，故M₃（-3，-1）.

点评  采用了“点的平移”这个模型后，解题快捷方便，在方法上，学生由被动接受变为主动探索，使学生能把以前所学的数学知识有机地结合起来.

“K”形模型

“K”形模型，是常见的“一线三等角”的相似模型（由三个等角的顶点在同一条直线上构成的相似图形，这个角可以是直角，也可以是锐角或者钝角）. 追溯其根源，可以归纳为三角形基架和矩形基架（如图2和图3所示）. “K”形模型在中考中出现的频率相当高.

例2 如图4，AB=4，射线BM和AB互相垂直，点D是AB上的一个动点，点E在射线BM上， 且BE=1/2BD，作EF⊥DE并截取EF=DE，连接AF并延长交射线BM于点C.  设BE=x，BC=y，则y关于x的函数解析式是（      ）

A. y=-12x/（x-4）               B. y=-2x/（x-1）

C. y=-3x/（x-1）                 D. y=-8x/（x-4）

分析  过点F作FG⊥BC于点G，则可构成“K”形模型.

点评  利用“K”形模型，关键是如何去构造这个模型，有时是“K”字相似，有时是“K”字全等. 教学中，我们要善于抓住此类问题的基础知识点和本质规律来提炼归类成简单的解题模型.

将军饮马模型

传说古罗马亚历山大城有一位精通数学和物理的学者，一天，一位罗马将军专程去拜访他，向他请教一个百思不得其解的问题：将军每天从军营B出发，先到河边饮马，然后再去河岸同侧的A地开会，如图5所示，应该怎样走才能使路程最短？

分析 饮水点C是动点，显然可以用构造对称点来解决问题. 只需连接A′B，与l的交点C，即为路程最短点.

解答  作点A关于l的对称点A′，连接A′B，A′B与l的交点C即为所求点.

评析  若取l上异于C点的点C′，显然AC′+BC′>A′B.

将军饮马模型的原理：在“图形的轴对称”一节中出现，根据两点之间线段最短的原理求最短距离的一个方法模型. 常用于解决最短路径问题.

例3 如图6，MN为⊙O的直径，A，B是⊙O上的两点，过A作AC⊥MN于点C，过B作BD⊥MN于点D，P为DC上的任意一点，若MN=20，AC=8，BD=6，则PA+PB的最小值是______.

分析  P为直径MN上的动点，将直径MN所在的直线看成是模型中的河流，A点和B点分别看成是山峰A和营地B，构造A或者B关于MN的对称点即可.

点评  该题型是“两定点在直线同侧，在直线上找到一点到两定点距离和最短”这一模型，也就是上文提到的“将军饮马”模型的简单应用.

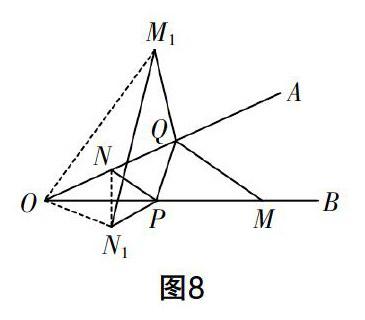
例4 如图7，∠AOB=30°，点M，N分别在边OA，OB上，且ON=1，OM=3，点P，Q分别在边OB，OA上，则NP+PQ+QM的最小值是______.

分析 学生刚接触到这个题目时，不知道如何去解，因为在他们的印象中，类似将军饮马问题都是“已知两个定点，求一个动点到它们之间的距离和最小”，而此题却是求两个动点到已知两个定点之间的距离和最小，好像无法使用我们熟知的模型了. 此时笔者引导学生，我们可以假设点Q固定，先求解NP+PQ的最小值，这时自然会联想到利用将军饮马的模型作点N关于OB对称的點N₁;接着求解PQ+QM的最小值，同样可以假设P点固定，也可以利用将军饮马的模型作点M关于OA对称的点M₁，分步骤来求解.

点评  本题渗透了转化、数学建模等思想，而主导思想在于转化，通过轴对称变换把该类问题转化为利用“两点之间线段最短”解决的问题，从而达到“化折为直”“化和为一”，将折线、线段的问题归结为直线问题的目的.

通过以上基本模型，我们发现在平时复习时，要善于提炼数学模型，当遇到数学问题时，首先辨认其属于哪一类基本模型，再利用模型探索解决问题的策略，这比单纯教会学生解题更为重要，意义更加重大.