排序集抽样下Pareto分布形状参数的Bayes估计

宗凤喜，李如兵,2

（1.曲靖师范学院 数学与统计学院，云南 曲靖 655011;2.上海财经大学 经济学院，上海 200433）

0 引言

排序集抽样是Mclntyre[1，2]首次提出的，在样本容量相同的情况下，与简单随机抽样相比，排序集抽样得到的样本包含更多的总体信息，从而能够对总体做出更准确的推断。有时候,对样本的测量可能比较困难,比如成本较高,或者花费时间较长,或者具有破坏性,但是通过简单的方法容易对样本的大小进行排序,比较适合用排序集抽样方法。很多学者都研究了基于排序集抽样的情况下,某些分布未知参数的Bayes估计。例如,Adatia[3]介绍了half-logistic分布在排序集抽样下的Bayes估计；Shaibu和Muttlak[4]介绍了在排序集抽样下正态分布、指数分布以及Gamma分布的Bayes估计和相关性质；Sinha等[5]研究了在排序集抽样下正态分布和指数分布参数的最优线性无偏估计；Stokes[6]研究了在排序集抽样下位置-尺度分布族参数的最大似然估计；Al-Saleh等[7]探讨了在排序集抽样下基于平方损失函数指数分布参数的Bayes估计，Sadek等[8]研究了在排序集抽样下指数分布参数的Bayes估计。

Pareto分布是意大利经济学家Pareto（1987）将其作为一种收入分布最先研究的，一个多世纪以来,被广泛应用在很多领域，比如，个人收入、城市人口、股票价格、保险风险、商业失效、某种药理过程后病人的存活时间等都可以用Pareto分布来描述。因此，研究Pareto分布具有重要的理论意义和实用价值。国内外很多学者都讨论过Pareto分布的性质：Abu-Dayyeh等[9]研究了排序集抽样下Pareto分布形状参数及尺度参数的最大似然估计、最小方差无偏估计；Omar等[10]研究了在极值排序集抽样下Pareto分布形状参数及尺度参数的矩估计以及最小偏差无偏估计；Ouyang等[11]对寿命分布为Pareto分布的n个元件进行定数截尾实验，当观测到有r个元件失效后，研究了剩余元件的失效时间以及还需要的实验时间的Bayes预测；李海芬和峁诗松[12]讨论了Pareto分布的R2检验法；李艳颖[13]在平方损失及Q-对称熵损失下给出了Pareto分布形状参数的贝叶斯估计，并讨论了估计的容许性；康会光等[14]和韦莹莹等[15]研究了Linex损失下Pareto分布族参数的经验Bayes估计。

本文针对Pareto分布的尺度参数，首先给出基于简单随机样本（SRS）下的Bayes估计，接着研究基于排序集样本（RSS）下的Bayes估计，最后通过Monte Carlo模拟来比较各种估计的偏差和均方误差，结果表明，相同条件下基于RSS得到的估计比基于SRS得到的估计更有效，并且在相同条件下基于共轭先验得到的估计比基于Jeffreys先验得到的估计更有效。

1 预备知识

设总体的概率密度和分布函数分别为f(x)，F(x)，容量为n的排序集样本按如下程序获得：首先从总体中获取容量为 n2个简单随机样本：X11，X12，…X1n;X21，X22，…，X2n;…;Xn1，Xn2，…，Xnn。对每组样本按从小到大的顺序进行排序：X(1)1，X(1)2，…X(1)n;X(2)1，X(2)2，…，X(2)n;…;X(n)1，X(n)2，…X(n)n。记Yi=X(i)i，i=1，2，…，n。则称Y1，Y2，…，Yn为一组只有一个循环的排序集样本,如将上述过程循环m次，则可以得到有m个循环的排序集样本：Y11，Y12，…Y1n;Y21，Y22.，…，Y2n;…;Ym1，Ym2，…，Ymn,简称 RSS。在上述获取RSS的过程中，如果假设排序过程中不存在误差，或误差非常小可以忽略不计，则Yi或Yjii=1，2，…，n;j=1，…，m的概率密度即为容量为n的简单随机样本（SRS）的第i个次序统计量的概率密度，具有如下表达式：

Pareto分布的概率密度和分布函数分别为如下表达式：

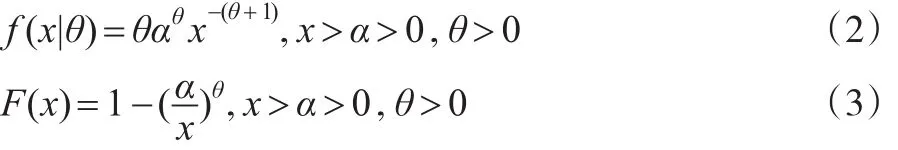
其中，θ为形状参数，α为尺度参数，也称为门限参数，在这里假设是已知的。

损失函数是Bayes估计中非常重要的一部分，下面给出本文中涉及到的三种损失函数：平方损失函数（squard error loss function）、Q-对称熵损失函数(Q-symmetric entropy loss function)、Linex 损失函数(Linex loss function),表达式分别为：

其中，δ是θ的估计值。

研究Bayes估计的前提是要给出待估参数的先验分布，本文主要考虑共轭先验分布即Gamma分布，以及Jeffreys先验分布,其表达式分别为：

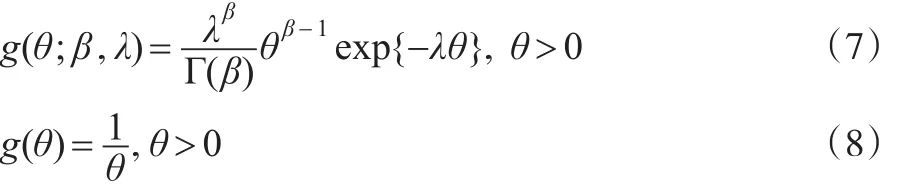
当β=λ=0，共轭先验分布就变成了Jeffres先验分布。

2 Bayes估计

设X1，X2，…，Xn为来自Pareto分布的简单随机样本（SRS），x1，x2，…，xn为相应样本的观测值；设Y1，Y2，…，Yn为来自Pareto分布的只有一个循环的排序集样本（RSS），y1，y2，…，yn为相应样本的观测值；Y11，Y12，…Y1n;Y21，Y22.…，Y2n;…;Ym1，Ym2，…，Ymn为来自Pareto分布的有m个循环 的 排 序 集 样 本 ，y11，y12，…，y1n；y21，y22，…，y2n;ym1，ym2，…，ymn为相应样本的观测值，本文用 π(θ|x)，π(θ|y)分别表示在给定SRS(X)和RSS(Y)下的参数θ的后验概率密度。

2.1 基于SRS的Bayes估计

基于SRS的Bayes估计,很多文献都进行了研究，这里只是以定理的形式列举出来，而要推导出定理中涉及的结论，要用到的关键内容以引理的形式给出，这些引理在后面推导基于RSS的Bayes估计时也要用到,并且下面的引理适用于任何分布的参数以及任何给定的先验分布。

引理1[16]：在给定先验分布及平方损失函数下，θ的Bayes估计为后验分布 π(θ|X)的均值，即：

并且该估计是唯一的，是可容许的。

引理2[13]：在给定先验分布及Q-对称熵损失函数下，θ的Bayes估计为：

并且该估计是唯一的，是容许的。

引理3[13]：在给定先验分布及Linex损失函数下，θ的Bayes估计为：

并且该估计是唯一的，是容许的.

下面以三个定理的形式给出基于平方损失、Q-对称熵损失以及Linex损失下θ的Bayes估计。

定理1[13]：在SRS和平方损失函数下：基于Gamma先验分布θ的Bayes估计为：

而基于Jeffreys先验分布的Bayes估计为：

定理2[13]:在SRS和Q-对称熵损失函数下，基于Gamma先验分布θ的Bayes估计为：

而基于Jeffreys先验分布θ的Bayes估计为：

定理3[13]:在SRS和Linex损失函数下，基于Gamma先验分布，θ的Bayes估计为：

而基于Jeffreys先验分布θ的Bayes估计为:

2.2 基于RSS的Bayes估计

定理4：在只有一个循环的RSS和平方损失函数下，基于Gamma先验分布θ的Bayes估计为：

而基于Jeffreys先验分布的Bayes估计为：

其中Cij(j)同上

证明：由式（1）至式（3）式可知Yj的概率密度为：

由于Y1，Y2，…，Yn是相互独立的，因此只有一个循环的RSS的联合概率密度为：

因此，当先验分布为Gamma分布时，θ的后验概率密度 π(θ|Y)有如下性质：

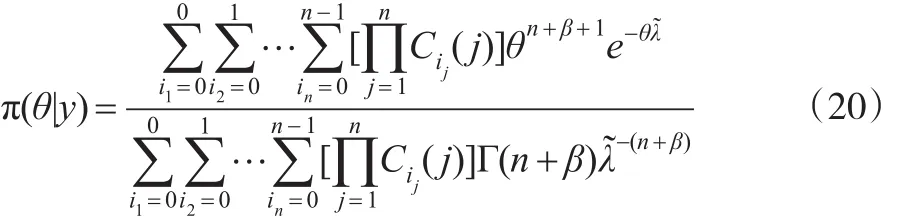
根据Gamma分布概率密度的性质，由引理1可得在只有一个循环的RSS和平方损失函数下，基于Gamma先验分布θ的Bayes估计为：

当上式中的β=λ=0时，可得在只有一个循环的RSS和平方损失函数下，基于Jeffreys先验分布的Bayes估计为：

定理5：在只有一个循环的RSS和Q-对称熵损失函数下，基于Gamma先验分布θ的Bayes估计为：

其中Cij(j)同上

而基于Jeffreys先验分布的Bayes估计为：

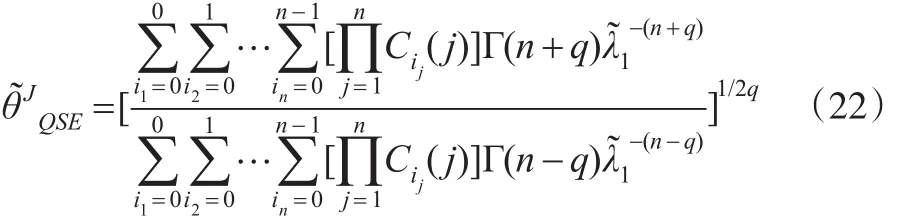
注：由引理2、定理4中的式（20）以及Gamma分布概率密度的性质，定理5很容易得到证明。

定理6：在只有一个循环的RSS和Linex损失函数下，基于Gamma先验分布θ的Bayes估计为：

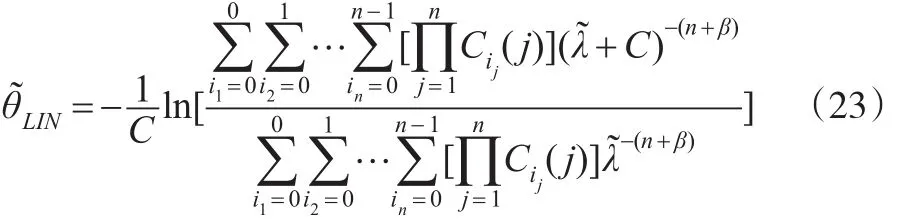
而基于Jeffreys先验分布的Bayes估计为：

与定理4中的相同。

注：由引理3、定理4中的式（20）以及Gamma分布概率密度的性质，定理6很容易得到证明。

下面介绍在有m个循环的RSS下Pareto分布尺度参数θ的Bayes估计。

定理7：在有m个循环的RSS和平方损失函数下，基于Gamma先验分布θ的Bayes估计为：

而基于Jeffreys先验分布的Bayes估计为：

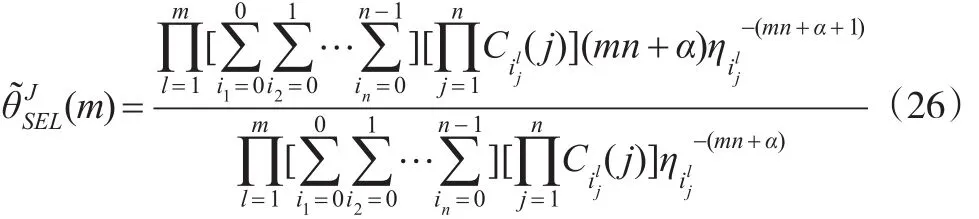
其中：

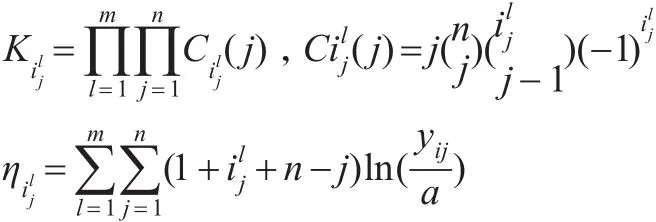
因此，当先验分布为Gamma分布时，θ的后验概率密度 π(θ|Y)有如下性质：

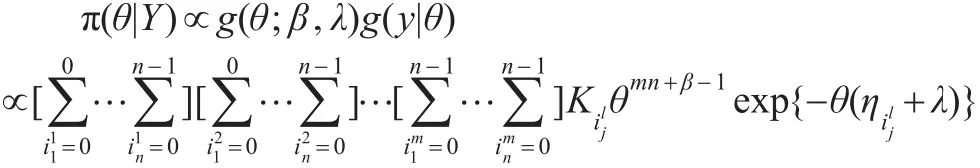
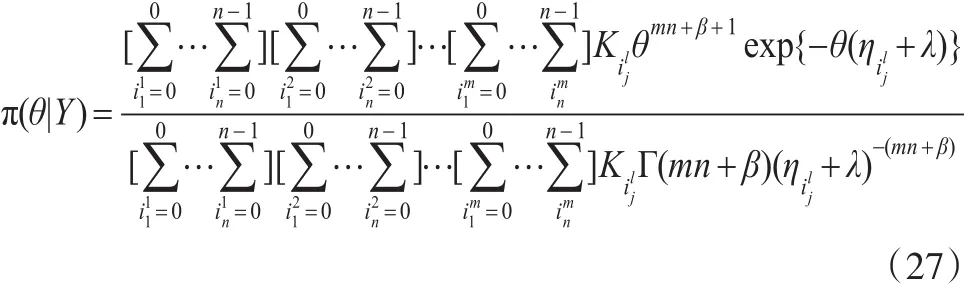
根据Gamma分布概率密度的性质，由引理1可得在有m个循环的RSS和平方损失函数下，基于Gamma先验分布θ的Bayes估计为：

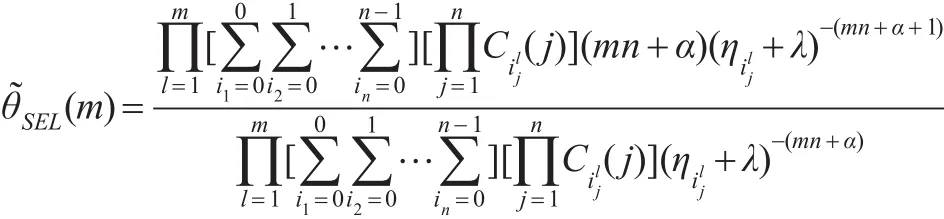
当上式中的β=λ=0时，可得在有m个循环的RSS和平方损失函数下，基于Jeffreys先验分布的Bayes估计为：

定理8：在有m个循环的RSS和Q-对称熵损失函数下，基于Gamma先验分布θ的Bayes估计为：

而基于Jeffreys先验分布的Bayes估计为：

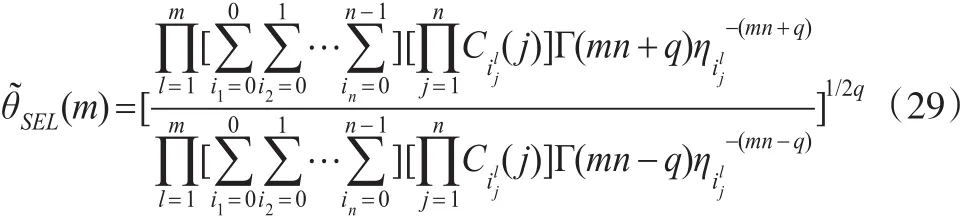
注：由引理2、定理7中的式（27）以及Gamma分布概率密度的性质，定理8很容易得到证明。

定理9：在有m个循环的RSS和Linex损失函数下，基于Gamma先验分布θ的Bayes估计为：

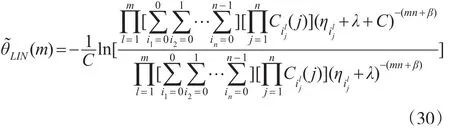
而基于Jeffreys先验分布的Bayes估计为：

注：由引理3、定理7中的式（27）以及Gamma分布概率密度的性质，定理9很容易得到证明。

3 数值模拟

在上文中，在Matlab中利用Monte Carlo法，通过比较偏差和均方误差来比较得到的各种估计的优劣，偏差与均方误差越小，估计就越好。借鉴文献[8],本文取n=3，4，5，6;λ=β=1;C=1，-1;关于Pareto分布，本文选取文献[10]中涉及到的一个真实模型：α=1.625，θ=2.314.q=1。模拟结果见下页表1和表2。

从表1发现，关于参数θ的所有Bayes估计都是有偏的，但偏差随着样本容量n的增加而减小；相同条件下，基于Gamma先验分布得到的参数θ的Bayes估计值与基于Jeffery先验分布得到的Bayes估计值相比，偏差要小一些；最重要的是，在相同条件下，基于RSS得到的参数θ的Bayes估计与基于SRS得到的Bayes估计相比偏差要小得多。

从表2发现，所有Bayes估计的均方误差随着样本容量n的增加而减小，符合点估计的一般要求；相同条件下基于Gamma先验分布得到的参数θ的Bayes估计值与基于Jeffery先验分布得到的Bayes估计值相比，均方误差明显的小很多；最重要的是，在相同条件下，基于RSS得到的参数θ的Bayes估计与基于SRS得到的Bayes估计相比，均方误差要小的多.当c=-1时，定理6中的式（24）对数中出现了负数，所以此时的偏差与均方误差都是复数，在表1和表2中复数没有列出。表1和表2的结果充分表明了，针对Pareto的形状参数，本文介绍的基于RSS的Bayes估计是有效的。

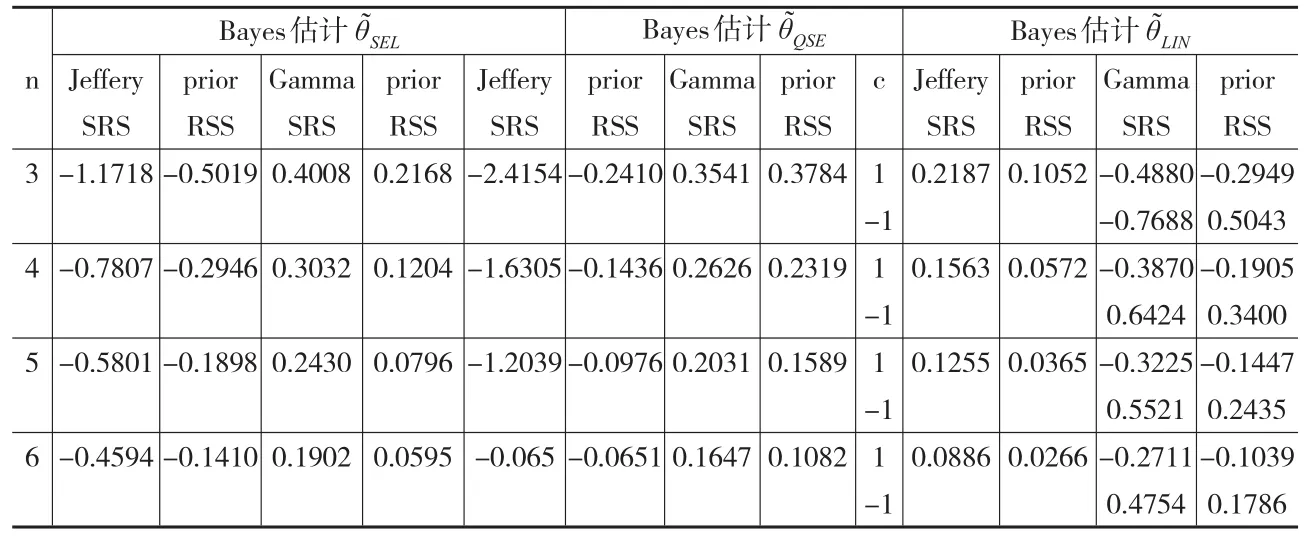
表1 Bayes估计的偏差

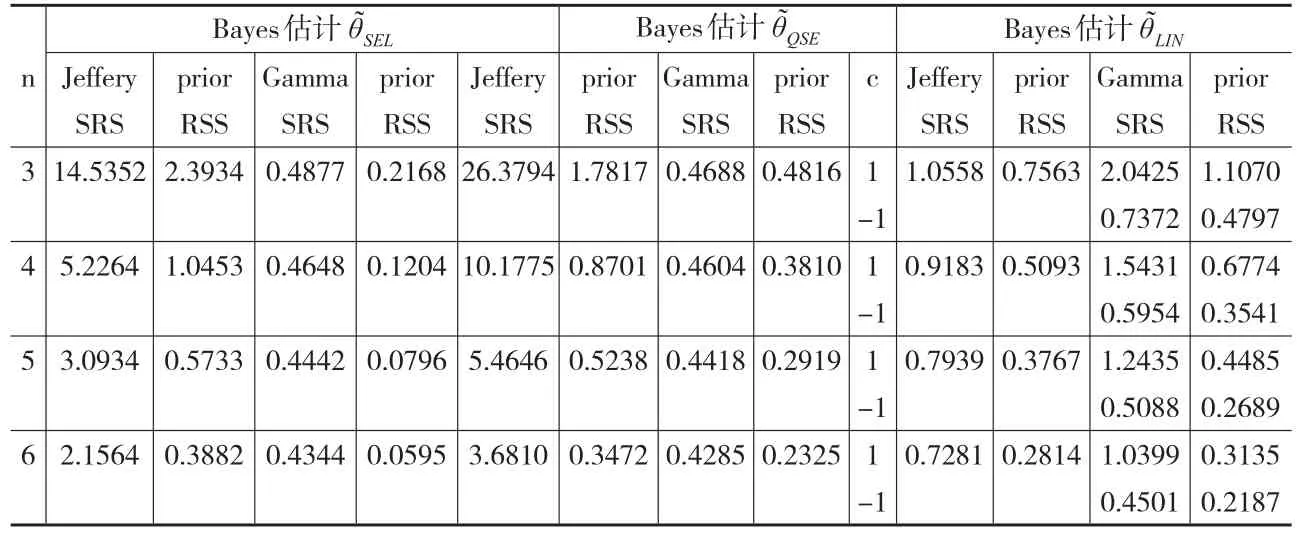
表2 Bayes估计的均方误差