圆锥曲线中最值问题的求解策略

■江苏省张家港职业教育中心校 韩文美

分析：利用椭圆的参数方程,结合圆心与椭圆上的点的距离公式求解,转化为三角函数问题,再利用三角函数的有界性确定最值。

解：设圆的圆心为C,则C的坐标为(0,

圆锥曲线中的求解最值问题一直是高考命题的热点,题型多,命题角度广,备受命题者青睐。虽然圆锥曲线中的最值问题形式多变,花样翻新,难度较大,但是基本解法仍有章可循,有法可依,概括来说:先根据题设条件,恰当选择某个与目标密切相关的自变量,并确定目标函数的解析式;在充分考虑函数的定义域、不等式的最值条件等前提下,应用函数的单调性、基本不等式定理及其推论进行分类讨论,从而达到求解圆锥曲线中的最值问题。下面就圆锥曲线中求最值问题的一些常见求解策略,结合实例进行剖析。

1.三角函数策略,有界性显身手

故答案为D。

点评:本题主要考查椭圆与圆的标准方程,椭圆的参数方程,两点间的距离公式等知识。通过圆与圆锥曲线的相关几何性质,结合对应的位置关系,以及三角函数的有界性来解决距离的最值问题,也是选择题或填空题中比较常见的题型。

2.基本不等式策略,变形转化显身手

分析：通过数形结合知:P在第一象限内,直线OM的斜率最大。设出相应的坐标,利用平面向量的线性运算与坐标运算加以转化,结合直线的斜率公式,利用基本不等式加以变形与综合,最后求解相应的最值问题。

图1

点评:本题主要考查抛物线的方程与几何性质,平面向量的线性运算与坐标运算,基本不等式,也考查了数形结合思想,以及同学们的运算能力。利用基本不等式来解决圆锥曲线中的最值问题是比较常见的一种思路,关键是通过题中条件加以转化,结合对应参数的取值情况,利用基本不等式来确定最值,注意基本不等式成立的条件。

3.数形结合策略,几何性质显身手

A.9,1 2 B.8,1 1

C.8,1 2 D.1 0,1 2

分析：通过数形结合,判定两圆圆心分别为椭圆的两个焦点A、B,结合椭圆的定义与对应的图形可判断最大值为|P A|+|P B|+2R,最小值为|P A|+|P B|-2R。

解：如图2,由椭圆及圆的方程可知两圆圆心分别为椭圆的两个焦点A、B,由椭圆定义知|P A|+|P B|=2a=1 0。

连接P A、P B,分别与圆相交于M、N两点,此时|PM|+|P N|最小,最小值为|P A|+|P B|-2R=8;

连接P A、P B并延长,分别与圆相交于M1、N1两点,此时|PM1|+|PN1|最大,最大值为|P A|+|P B|+2R=1 2。

因此,所求最小值和最大值分别为8,1 2,答案为C。

点评:本题考查椭圆与圆的方程,椭圆的定义,以及数形结合思想在解决问题中的应用。巧妙利用数形结合思想,可以化代数为几何,把复杂问题直观化,更加有效地解决圆锥曲线中的最值问题。

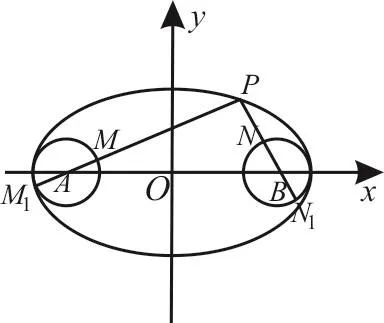
图2

4.极限思维策略,极端确定显身手

分析：根据双曲线的定义可知|P F1|=|P F2|+2,通过分类讨论,结合极限思维确定当∠F1P F2=9 0°时与当∠F1F2P=9 0°时关系式的最值,数形结合即可得△F1P F2为锐角三角形时关系式的取值范围。

解：由题可得a=1,b=3,c=2。由双曲线的定义知|P F1|―|P F2|=2a=2,则有|P F1|=|P F2|+2。

当∠F1P F2=9 0°时,|P F1|2+|P F2|2=|F1F2|2,可得|P F2|2+2|P F2|―6=0,解得|P F2|=7―1或-7-1(负值舍去),此时|P F1|+|P F2|=2 7;

当∠F1F2P=9 0°时,|P F1|2=|P F2|2+|F1F2|2,解得|P F2|=3,此时|P F1|+|P F2|=8。

若△F1P F2为锐角三角形,数形结合可得|P F1|+|P F2|∈(2 7,8)。

点评:本题主要考查双曲线的定义、标准方程与几何性质,以及焦点三角形。极限思维是一种重要的数学思想,应用极限法来解决一些选择题时,可以避开繁杂的运算过程,独辟蹊径,降低解题难度,优化解题过程,起到事半功倍的效果。

圆锥曲线中的最值问题类型较多,解法灵活多变,但总体上主要有两类:一是利用几何方法,即利用曲线的定义、几何性质以及平面几何中的定理、性质等求解;二是利用代数方法,即把要求最值的几何量或代数表达式表示为某个(些)参数的函数(解析式),然后利用函数方法、不等式方法等进行求解。

(责任编辑 徐利杰)