隧道结构内列车风荷载下接触网系统的风致振动响应

杨伟超，何川，彭立敏，雷明锋，张平平

(1. 西南交通大学 土木工程学院，四川 成都 610031；2. 中南大学 土木工程学院，湖南 长沙 410075)

高速铁路隧道内列车风风速大，行车密度高，接触网系统的风致振动成为一个突出问题。接触网通过吊柱与隧道拱顶衬砌连接，其频繁往复振动会引起隧道衬砌结构出现应力损伤，进一步会导致拱顶衬砌结构疲劳和失稳等。列车风一直是高速铁路隧道气动效应的重要研究内容。20世纪70年代和80年代Pope 等[1-2]在英国的Patchway隧道和法国的Rilly-La-Montagne隧道(均为单线，无竖井)内进行隧道压力波和活塞风的现场实测。Gilbert等[3]采用1:25动模型分析4节ICE2列车驶入隧道时的列车风时程和峰值分布。长期以来，我国在隧道通风工程中均采用“活塞作用系数”法计算活塞风速度[4]；20世纪80年代，史力生[5]采用理论分析和现场实测的方法，通过对活塞风衰减规律进行分析得到双线铁路隧道内沿程阻力系数；李炎等[6-7]通过理论分析的方法，建立隧道内流场的连续性方程、能量方程和动量方程，确定单线、无竖井、横通道及斜井的隧道内活塞风风压的基本控制方程，提出针对高速铁路隧道内列车风的一维计算方法。李人宪等[8]采用数值计算方法，提出列车风对人体最大水平作用力计算关系式和人体附近最大列车风速计算关系式，同时提出高速列车附近人体安全距离的建议。费瑞振等[9]采用数值模拟方法对高速列车在隧道内运行时列车风的变化规律和分布特征进行研究，计算隧道内两侧疏散通道上不同位置在列车运行过程中的最大风速，分析在列车风作用下人员的安全性。谭鹏等[10]采用数值模拟方法对列车在城际铁路隧道内运行过程中所产生的列车风变化过程进行分析，计算高速列车在隧道内运行时隧道内沿纵向不同位置列车风最大风速，并对隧道内列车风纵向和横向分布特性进行探讨。但以上研究主要基于隧道内作业人员安全方面，研究对象主要集中在风速、风向和时空特性等列车风本身特性方面，对列车风荷载下隧道内附属设施的动力响应和累积损伤的研究相对较少。接触网系统是高速铁路的生命线工程，也是影响我国铁路运输安全畅通的五大设备故障之一[11-12]。隧道内接触网一般采用吊柱形式固定在拱顶，而隧道拱顶结构相对薄弱，密实性和背后空洞等初始损伤问题一直比较突出。在列车风荷载的作用下，接触网支(吊)柱、腕臂、预埋滑道轨槽、螺栓或隧道衬砌等处会出现应力集中区，并出现裂纹[13]，在多次重复变化的荷载作用下，在裂纹的尖端形成尖锐的缺口，又造成新的应力集中区。在循环荷载的连续作用下，裂纹会越来越大，构件上能够承受应力的面积越来越小，直至最终突然破坏。根据万晓燕等[14]在遂渝线提速综合气动试验结果，当列车以200 km/h速度突入松林堡隧道和荆竹岭隧道时，隧道内列车风分别达到19.7 m/s和17.1 m/s，风速相当于可摧毁树枝的8级大风。目前，我国高速铁路干线的运营速度可达 250~380 km/h，列车风荷载对隧道内附属设施的影响不容忽视。本文以高速铁路隧道内接触网为研究对象，建立列车-接触网-隧道结构-空气的精细化计算模型，通过流固耦合计算的方法，分析高速铁路隧道内列车风的时空变化规律，研究列车风荷载作用下隧道内接触网系统的动位移、加速度和振型等动力响应特性，研究结果对高速铁路隧道内接触网的设计和施工提供参考，也为以后隧道衬砌结构的动力和耐久性设计提供理论依据。

1 计算方法及模型

列车风荷载作用下接触网系统的振动属于典型的流固耦合问题，首先在列车分荷载下接触网会产生变形或运动，而接触网的变形和运动反过来又影响列车风的分布和运动。流固耦合的控制方程包括流体控制方程、固体动力方程和流固耦合方程。

1.1 流体控制方程

流体控制方程由质量守恒定律、动量守恒定律、能量守恒定律等组成。列车风属于可压缩牛顿流体，控制方程可采用Arbitrary Lagrangian Eulerian(ALE)格式的的非定常可压缩N-S方程[15]为：

式中：W为守恒量；F(W)和Fv分别为无黏和黏性矢通量；vgn为法向运动速度，具体表达式和各变量物理意义见文献[15]。

湍流模型采用标准的K-ε双方程，湍动能(k)方程为：

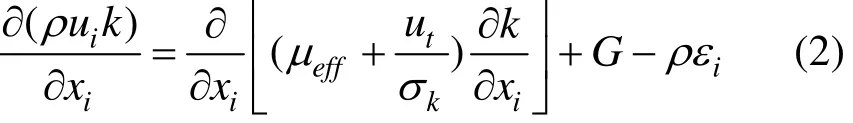
湍动能耗散率(ε)方程

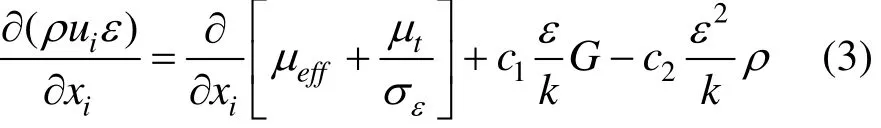
1.2 接触网系统动力方程

列车风荷载诱发的接触网系统动力方程由牛顿第二定律导出[16]：

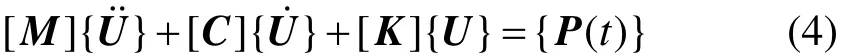
其中：M为质量矩阵；C为阻尼矩阵；K为刚度矩阵；P(t)为结构外载荷；U为t时刻节点的位移向量。结构动力学方程采用Newmark法求解。

1.3 流固耦合方程

在流固耦合交接面处，应满足流体与固体切应力τ，位移d，热流量q和温度T等变量的相等或守恒，满足如下4个方程：

其中：下标f表示流体；下标s表示固体。

1.4 计算模型

铁路隧道内接触网悬挂的安装方式主要有 2种[17]：1)二衬浇注完成后钻孔并采用锚栓固定；2)在二衬施工时预埋滑道，接触网悬挂直接在滑道上安装固定。本文采用第1种安装方式，结构布置图如图1所示。隧道内接触网系统包括定位还是反定位2种型式，其均由平腕臂、斜腕臂、定位管、腕臂支撑、套管单耳和管帽等组成。反定位的跨度相对较大，其风致振动效应更为显著，本文以反定位为背景进行研究。

图1 接触网结构布置图Fig. 1 Layout of contact networks system

隧道混凝土衬砌和接触网支持结构采用实体单元建模，如图2所示。大气选用标准理想气体，隧道衬砌采用C35混凝土，接触网采用Q235A热轧型钢，力学参数如表1所示。

表1 衬砌及接触网系统力学参数Table 1 Mechanical parameters of lining and contact networks system

1.5 边界条件

列车、隧道内壁和接触网壁面设置为无滑移墙边界；接触网与隧道相连部分的壁面设置为固定约束，接触网与大气相连部分的壁面设置为流固耦合面；流体和固体中的接触网处壁面通过数据传递联系。接触网除受到气动荷载外，还受到接触线曲线力Fj，承力索力Fc和重力G，根据文献[11]的计算方法，分别取Fj为3.01 kN，Fc为2.11 kN，直接施加在相应受力位置，重力G通过材料密度实现。

列车以时速 350 km/h的速度突入单线双洞隧道，列车与隧道相对运动采用动网格方法实现。接触网壁面设置为系统耦合区域，隧道与接触网相连部分的壁面设置为变形区域。流体部分、固体部分和流固耦合部分数值计算的时间步长和耦合滞至时间保持一致。

图2 隧道接触网系统计算模型Fig. 2 Calculation model of tunnel contact networks system

2 接触网系统的振动响应特性

以列车速度350 km/h驶过单线双洞隧道(隧道长度500 m，断面积70 m2)时的计算结果，对接触网和隧道结构的振动特性进行分析。

2.1 接触网系统主振型

模态分析是瞬态动力学分析的基础，下面对接触网系统的各阶模态的特性进行分析，图3为列车风作用下接触网结构振动的前6阶振型。

由图 3 的结果可以看出，第 1阶振型为接触网支持结构在平腕臂和定位管的带动下沿隧道纵向前后摆动，摆动时两者方向一致，频率为 4.01 Hz；第2阶振型为接触网支持结构在平腕臂和定位管的带动下沿隧道纵向前后摆动，摆动时两者方向相反，频率为11.14 Hz；第3阶振型为接触网支持结构在吊柱的带动下沿隧道横向左右摆动，频率为13.83 Hz；第4阶振型为接触网支持结构在吊柱的带动下沿隧道纵向前后摆动，频率为15.57 Hz。第5阶和第6阶振型为局部振动，分别表现为定位管的前后和上下摆动，频率为19.56 Hz和23.33 Hz。

图3 接触网支持结构振型图Fig. 3 Vibration mode of the contact networks structure

由模态分析的结果可知：接触网支持结构的自有振型以前后振动为主，其频谱比较密集，既有对称振型，又有反对称振型；而左右摆动的自有振型相对较少，另外对于定位管附近，则出现上下和前后振型。整体上，列车风荷载作用下接触网系统振动主要表现为：以沿着隧道纵向的前后摆动为主，左右摆动和扭转为辅的复杂振动特性。

2.2 接触网振动位移

图4为接触网系统定位管的动位移响应结果。

图4 接触网定位器处动位移时程变化Fig. 4 Time-history of displacement of the contact network locator

从图4的计算结果可知：

1) 定位器的动位移在列车风开始增加时接触网定位器开始出现振动，但此时的列车风风速较小，振动幅度相对也相对较小；随着车头达到定位器，风速开始加大，定位器的振动速度也开始增大；当列车车尾经过后，接触网定位器的振动开始减小，但此时隧道内尚有列车风，接触网在风荷载的作用下保持一定振动。

2) 接触网的振动方向与列车风幅度与列车风各分量的风速幅度基本一致，其中沿纵向列车风风速较大，因此振动位移也相对较大，其次为横向振动，而竖向振动相对很小，可以忽略，由于隧道内的列车风主要是沿着隧道的纵向方向分量，因此接触网的振动方向也主要是沿着列车的运行方向。

3) 定位器的纵向最大动位移约为148.2 mm，出现在车尾经过时，横向最大位移约为112.3 mm，出现在车头经过时，竖向列车风最大动位移约为2.6 mm，出现在车头经过时，合风速的最大位移约为166.2 mm，出现在车尾经过时。

2.3 接触网振动加速度

图5为接触网定位管的振动加速度响应结果。

从上述计算结果可知：

1) 定位器的加速度在车头到来前约1 s开始出现变化，最大的振动范围主要在列车车体经过时间段，随着车尾的经过，隧道内风速减小，定位器的振动加速度变化量也开始减小，在约1.5 s后基本恢复到近似静止状态。

2) 定位器的振动加速度的峰值与位移的峰值基本保持一致，其中纵向最大动位移约为139.4 m/ s2，出现在列车车尾经过时，横向最大位移约为-109.5 m/s2，出现在车头经过时，竖向列车风最大动位移约为 1.6 m/s2，出现在车头经过时，合风速的最大位移约为 140.8 m/s2，出现在列车车尾经过时间附近。

图5 接触网定位器处加速度时程变化Fig. 5 Time-history of acceleration of the contact network locator

3 隧道衬砌的振动响应特性

以螺栓连接处的衬砌混凝土为研究对象，分析列车风荷载作用下接触网连接处衬砌混凝土的气固耦合振动响应。接触网吊柱通过法兰盘和螺栓与隧道相接，则螺栓处的应力相对更大。定义如下测点，沿着列车行驶方向第1排，且远离隧道中心线的螺栓为1号，靠近隧道中心线的螺栓为2号，与1号螺栓对应的为3号，另外一处为4号，具体示意如图6所示。

3.1 接触网附近衬砌动应力

图7为列车以速度350 km/h驶过单线双洞隧道(隧道长度500 m，断面积70 m2)时，1号螺栓前后左右4个方向上衬砌表面混凝土的动应力响应时程曲线。

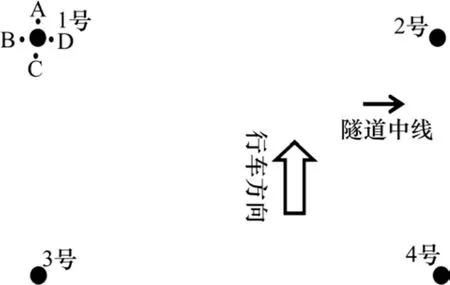
图6 接触网与衬砌混凝土连接处测点布置Fig. 6 Measuring points arrangement in connection between the contact network and the lining concrete

图7 接触网连接处衬砌表面的动应力时程Fig. 7 Time-history of dynamic stress in connection between the contact network and the lining

由以上结果可以看出：

1) 在螺栓附近各个方向上动应力时程曲线变化规律基本一致，即在列车风刚开始出现时，衬砌的动应力逐渐增大，到列车车体经过时动应力达到最大值，之后动应力开始逐渐减小，即衬砌结构的动应力与列车风的变化幅度基本是相互对应的；

2) 不同方向上的动应力峰值存在一定差异，靠近测点A处的动应力达到0.276 MPa，测点C的动应力达到约0.23 MPa，这与列车风的主要是由沿着隧道纵向的分量相对较大是相吻合的，而在横向的分量相对较小，因此，测点B和测点D的动应力相对较小。

3) 沿着列车运行方向，动应力最大值出现在车头经过时，如测点A和测点C；而垂直于列车运行方向，动应力最大值出现在车尾经过时。

4) 相对于列车荷载作用，气动荷载作用下衬砌结构的动应力变化幅度相对更大，其主要原因在于气动荷载是通过接触网的振动作用于衬砌结构，而接触网结构呈下悬状态，列车风作用下其振动幅度相对较大，从而传递较大幅度的交变振动荷载。

3.2 接触网附近衬砌加速度

图8为列车以速度350 km/h驶过单线双洞隧道(隧道长度500 m，断面积70 m2)时，为1号螺栓附近A点附近衬砌表面混凝土的加速度响应时程。

由以上结果可以看出：

1) 与接触网的加速度变化时程类似，螺栓附近衬砌混凝土的加速度变化与气动荷载的变化过程相一致，即在列车风刚开始出现时，衬砌的加速度逐渐增大，到列车车体经过时达到最大值，之后动应力开始逐渐减小；纵向加速的峰值出现在车尾经过时，横向和竖向加速度的峰值出现在车头经过时，最后的合成加速度峰值出现在车头经过时。

2) 加速度方向变化量与列车风各分量的特征相一致，对列车风各个风速分量中，风速峰值大小为：纵向分量>横向分量>竖向分量，因此衬砌混凝土加速度的各方向分量也表现出相似的规律，即：纵向分量>横向分量>竖向分量。

3) 由于接触网系统和衬砌混凝土的受力环境和约束条件的差异，相对于接触网定位器的加速度峰值，衬砌混凝土加速度峰值相对较低，其中衬砌结构的各分量加速度(纵、横向和竖向)峰值分别为1.62，1.77和0.28 m/s2，仅相对于接触网定位器的加速度分量(纵、横向和竖向峰值分别为139.4，109.5和1.6 m/s2)1.16%，1.62%和17.5%。

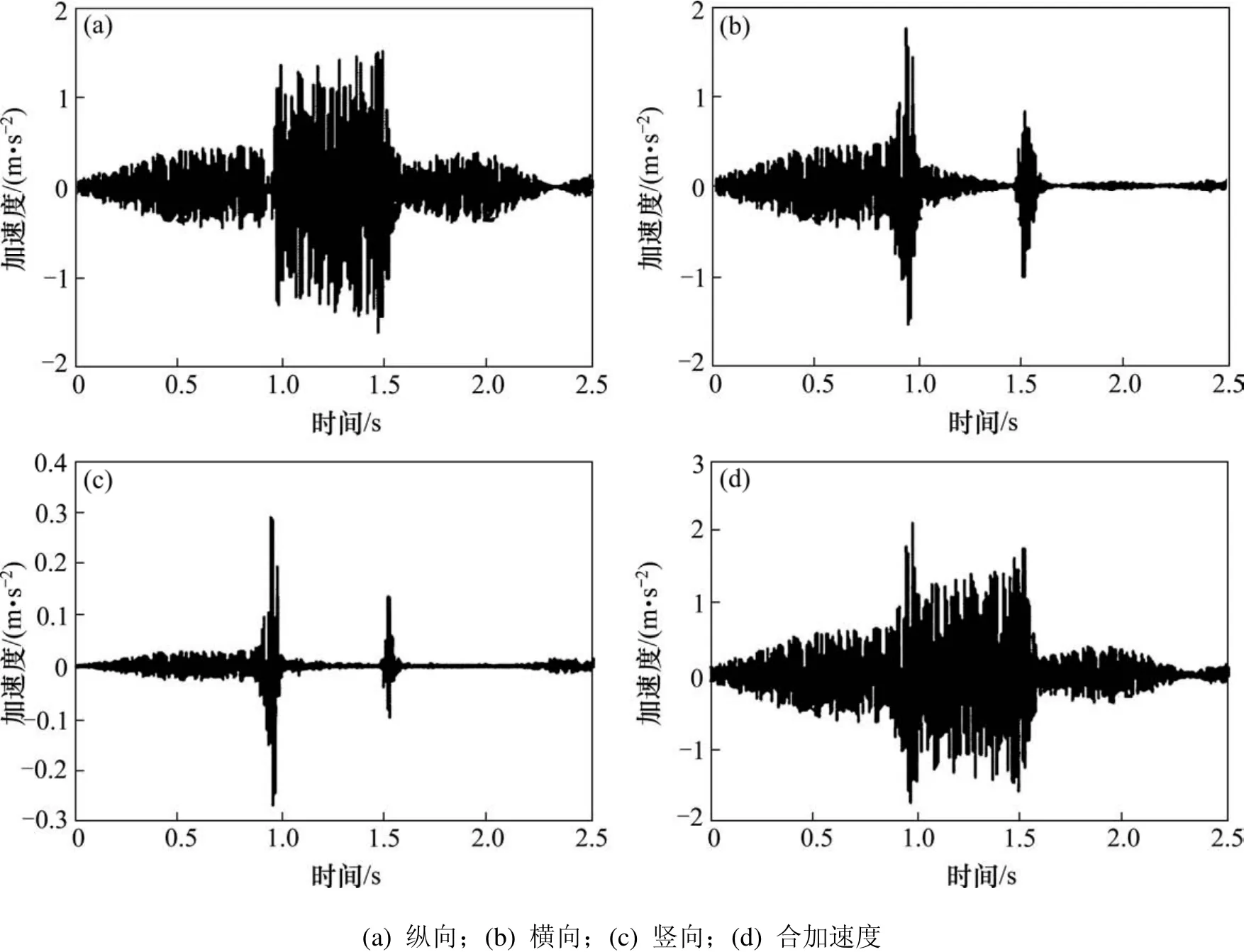
图8 接触网连接处衬砌表面的振动加速度时程Fig. 8 Time-history of vibration acceleration in connection between the contact network and the lining

4 结论

1) 列车风荷载作用下接触网系统振动主要表现为以沿着隧道纵向的前后摆动为主，左右摆动和扭转为辅的振动效应，其中第1，2和4阶振型的主振频率分别为4.01，11.14和15.57 Hz，均沿隧道纵向前后摆动；第3阶振型的主振频率为13.83 Hz，沿隧道横向左右摆动。

2) 接触网系统的动位移和加速度的振动时间与振幅均与列车风相一致，即接触网系统的振动与列车风出现同步，车头达到风速开始加大，振动位移、速度和加速度同时开始增大，在车尾经过时达到最大值。各分量的幅度大小顺序为：纵向分量>横向分量>竖向分量。

3) 螺栓附近衬砌的动位移和加速度的振动时间也与接触网系统和列车风的变化趋势基本一致，其中沿隧道纵向的动应力相对较大，沿隧道横向的动应力相对较小；相对于接触网系统，衬砌的动位移的主频相对较少。

[1] Pope C W, Gawthorpe R G, Richards S P. An experimental investigation into the effect of train shape on the unsteady flows generated in tunnels[C]// Proc. 4th ISAVVT, York, UK, BHRA Fluid Engineering, Paper C2,1983: 107-127.

[2] Gawthorpe R G, Pope C W. The measurement and interpretation of transient Pressures generated by trains in unnels[C]// Proc 2th ISAVVT, Cam bridge, UK, BHRA Fluid Engineering, Paper C3, 1976: 35-54.

[3] Gilbert T, Baker C J, Quinn A. Gusts caused by high-speed trains in confined spaces and tunnels[J]. J Wind Eng Ind Aerodyn, 2013(121): 39-48.

[4] 李涛. 活塞风对地铁车站内环境的影响[D]. 天津: 天津大学, 2005.LI Tao. The effect of piston wind on the inner environment of subway station[J]. Tianjin: Tianjin University, 2005.

[5] 史力生. 双线铁路隧道的活塞风和沿程阻力系数[J].铁道学报, 1995, 17(2): 113-125.SHI Lisheng. Piston wind and resistance factor of double track railway tunnel[J]. Journal of the China Railway Society, 1995, 17(2): 113-125.

[6] 李炎, 高孟理, 周鸣镝, 等. 列车与隧道环隙空间流场特性的研究[J]. 铁道学报, 2009, 31(6): 140-147.LI Yan, GAO Mengli, ZHOU Mingdi, et al.Characteristics of flow field in annulus space between train and tunnel[J]. Journal of the China Railway Society,2009, 31(6): 140-147.

[7] 李炎, 高孟理, 周鸣镝, 等. 铁路隧道列车活塞风的理论研究与计算方法的探讨[J]. 铁道学报, 2010, 32(6):117-121.LI Yan, GAO Mengli, ZHOU Mingdi, et al. Theoretical study and caculation method of train piston wind in railway tunnels[J]. Journal of the China Railway Society,2010, 32(6): 117-121.

[8] 李人宪, 赵晶, 张曙, 等. 高速列车风对附近人体的气动作用影响[J]. 中国铁道科学, 2007, 28(5): 98-104.LI Renxian, ZHAO Jing, ZHANG Shu, et al. Influence of the aerodynamic force to human body near high-speed trains[J]. China Railway Science, 2007, 28(5): 98-104.

[9] 费瑞振, 彭立敏, 施成华, 等．高速铁路双线隧道列车风特性与人员安全性分析[J]. 郑州大学学报(工学版)，2013, 34(4): 5-9.FEI Ruizhen, PENG Limin, SHI Chenghua, et al.Characteristics of train wind and analyses of personnel security in high-speed railway double-line tunnel[J].Journal of Zhengzhou University (Engineering Science),2013, 34(4): 5-9.

[10] 谭鹏, 彭立敏, 施成华, 等. 城际铁路隧道列车风特性及对人员安全的影响分析[J]. 中南大学学报(自然科学版), 2013, 44(4): 1557-1563.TAN Peng, PENG Limin, SHI Chenghua, et al.Characteristics of train wind and analysis of personnel security in inter-city railway tunnel[J]. Journal of Central South University (Science and Technology), 2013, 44(4):1557- 1563.

[11] 于万聚. 高速电气化铁路接触网[M]. 成都: 西南交通大学出版社, 2003.YU Wanju. High speed electrified railway catenary[M].Chengdu: Southwest Jiaotong University Press, 2003.

[12] 孙德忠. 提高接触网受电弓系统运行可靠性的研究[J].铁道机车车辆, 1996(3): 51-53.SUN Dezhong. Research on improving the operating reliability of catenary pantograph system[J]. Railway Locomotive & Car, 1996(3): 51-53.

[13] 费瑞振, 彭立敏, 杨伟超, 等. 高速铁路隧道空气动力效应对人员安全的影响研究[J]. 中国安全科学学报,2013, 23(7): 79-84.FEI Ruizhen, PENG Limin, YANG Weichao, et al. Study on aerodynamic force effect on personnel safety in high-speed railway tunnel[J]. China Safety Science Journal, 2013, 23(7): 79-84.

[14] 万晓燕, 吴剑. 时速200 km动车组通过隧道时空气动力学效应现场试验与研究[J]. 现代隧道技术, 2006,43(1): 43-48.WAN Xiaoyan, WU Jian. In-situ test and study on the aerodynamic effect of the rolling stock passing through tunnelsw ith a speed of 200 km/h [J]. Modern Tunnelling Technology, 2006, 43(1): 43-48.

[15] 肖天航. 低雷诺数非定常流场的数值方法及其在微型飞行器上的应用[D]. 南京: 南京航空航天大学, 2009.XIAO Tianhang. A numerical method for unsteady low reynolds number flows and application to micro air vehicles[D]. Nanjing: Nanjing University of Aeronautics and Astronautics, 2009.

[16] Ray W Clough, Joseph Penzien. Dynamics of structures[M]. 3rd ed. Computers & Structures, Inc, Berkeley, USA,2003.

[17] TB10003—2016, 铁路隧道设计规范[S].TB10003—2016, Code for design on tunnel of railway[S].