基于交叉熵和空间分割的全局可靠性灵敏度分析

赵翔，李洪双

南京航空航天大学 航空宇航学院，南京 210016

在结构和系统随机不确定性分析领域，灵敏度分析作为一个新热点，旨在研究输入不确定性如何影响系统的输出不确定性[1]。灵敏度分析可分为局部灵敏度[2]和全局灵敏度[3]两种。局部灵敏度通常定义为输入变量取名义值时系统功能函数对该变量的偏导数[2]，因而其不能反映输入变量的完整不确定性范围对输出响应不确定性的影响。全局灵敏度可以从输入变量的整个定义范围衡量该变量对输出不确定性的贡献程度，因此更加具有实际应用潜能。

全局灵敏度能够基于输入变量对输出响应不确定性影响程度的大小，对它们进行重要度排序，从而对结构和系统可靠性分析、预测与优化提供指导。全局灵敏度分析方法主要包括：非参数方法[4-5]、基于方差的方法[6-7]以及矩独立方法[8]。非参数方法仅适用于线性输入输出关系，缺乏模型的独立性。虽然基于方差的方法满足全局灵敏度指标的定义标准，即全局性、可量化性和通用性[3]，但该方法使用方差(即二阶矩)来表征不确定性信息，不可避免地会带来分布信息的损失[9]。为了反映输入变量对输出响应整个分布的影响，Borgonovo[8]提出了矩独立全局灵敏度指标，该指标不仅满足“全局性、可量化性、通用性”，同时也满足“矩独立性”。在矩独立灵敏度指标的基础上，Cui等[10]提出了基于失效概率的全局灵敏度指标，即全局可靠性灵敏度指标，以此来衡量输入变量的不确定性对结构失效概率的影响程度。Li等[11]推导了该指标与基于方差的重要度指标之间的关系,为可靠性灵敏度分析的计算提供了一条可行的新途径。然而，如何高效准确地计算全局可靠性灵敏度指标仍是目前亟待解决的问题。

目前基本求解方法主要分为两种：代理模型方法[12]和数字模拟方法[13]。前者使用代理模型逼近系统的输入随机变量与输出响应之间的关系，之后基于该代理模型计算灵敏度指标，该方法极大地提高了计算效率，但其计算精度主要依赖于代理模型的准确性。数字模拟法在失效概率评估和重要度分析上具有较好的相容性，因此在基于失效概率的全局灵敏度研究中，数字模拟法更为通用。Wei等[13]给出了3种计算基于失效概率的全局重要度的数字模拟法，包括蒙特卡罗仿真(Monte Carlo Simulation，MCS)法、重要抽样(Importance Sampling，IS)法和截断重要抽样(Truncated Importance Sampling，TIS)法。3种方法之中，重要抽样方法和截断重要抽样方法计算效率较高，但是设计点个数及其位置求解困难，以致重要抽样密度函数难以确定，导致应用范围受到限制。在文献[13]的基础上，任超和李洪双[14]使用交叉熵方法计算失效概率全局灵敏度指标，有效地解决了传统重要抽样法中重要抽样函数难以确定的困难，但此算法的计算量仍然与输入随机变量的维数相关，对于高维问题以及复杂的工程模型，计算量依然是一个巨大的挑战。显然，在数字模拟法中，每个样本均包含所有输入变量的相关信息，但以往的处理方法不能最大限度地利用每个样本所包含的信息，样本利用率低，导致计算量与问题维数有关。

针对现有方法的不足，本文提出一种将交叉熵方法[15-16]和空间分割方法[17-20]相结合的新全局可靠性灵敏度分析方法。该方法使用交叉熵方法自适应的确定重要抽样密度函数，从而避免确定设计点个数及位置。通过新重要抽样密度函数增加样本落入失效域的概率，提高抽样效率。再对所得的重要抽样样本进行不同的划分进而得到各个变量的全局灵敏度指标。通过数值算例和工程算例的计算结果可以看出：本文所提方法解决了重要抽样函数难以确定的问题，并且只需重复利用一组样本，即可计算出所有变量的可靠性灵敏度指标，计算量与问题维数无关，大大提高了样本利用率。

1 基于失效概率的全局灵敏度分析

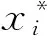
(1)

式中:E(·)为期望算子；fXi(xi)为输入随机变量Xi的概率密度函数。失效概率PfY的定义为

(2)

式中:fX(x)为输入随机变量X的联合概率密度函数，IF为失效域指示函数，其定义为

IF=1g(X)≤0

0g(X)>0

(3)

类似于无条件失效概率，条件失效概率PfY|Xi可以表示为

PfY|Xi=E(IF|Xi)

(4)

将式(2)和式(4)代入式(1)中，可将基于失效概率的全局灵敏度指标转变为以IF为输出的基于方差的全局灵敏度指标[11]：

V(E(IF|Xi))

(5)

式中：V(·)为方差算子。

Wei等[13]通过添加一个常数项V(IF)，使得基于失效概率的全局灵敏度分析和基于方差的全局灵敏度分析在形式上得到统一，即基于失效概率的全局灵敏度指标的方差形式：

(6)

式中：Si为一阶灵敏度指标。

对式(6)使用全期望公式和全方差公式，式(6)可进一步化为

(7)

2 新全局可靠性灵敏度分析方法

由第1节可知：式(1)转化为式(6)的形式后，可以将基于方差的重要度指标计算方法应用至全局可靠性灵敏度指标的计算之中。因此，可以使用高效的抽样算法计算原本比较难以求解的积分问题。进一步，由式(7)可知：选用一种能够高效计算失效概率PfY的抽样方法，可以大大降低计算量。

直接使用蒙特卡罗法，概念简单，容易编程实现，适应范围广，对问题的维数和复杂性没有特殊要求。但是对于失效概率很小的结构或者系统，直接蒙特卡罗方法必须使用大量的随机样本才能保证估计值收敛，计算效率低下。

重要抽样法在直接蒙特卡罗方法的基础上引入重要抽样密度函数hX(x)，提高了随机样本出现在“失效域”的频率，进而提高了抽样效率。式(2)所示的概率积分可以表示为

(8)

重要抽样法通常是将抽样中心选择在设计点处，使更多的样本点落入失效域，因此有着较高的抽样效率。但在实际应用过程中，该方法对于多设计点问题或者非线性程度较大的情况，设计点难以求解，重要抽样密度函数构造困难。然而实际上重要抽样密度函数的好坏将直接影响计算结果的精度和效率。

交叉熵方法(Cross Entropy Method)是一种自适应的重要抽样法，其概念由Rubinstein[15]于1997年最先提出用于稀疏事件的模拟，随后Rubinstein[16]又将其拓展为随机优化方法。交叉熵方法的主要思想是移动抽样中心至对失效概率贡献较大的区域，这与传统重要抽样方法相同。不同之处在于：交叉熵方法采用序贯方式确定重要抽样密度函数，避免了重要抽样法中重要抽样密度函数难以确定的困难。

2.1 交叉熵方法

设fX(x)和hX(x)是给定的2个概率密度函数，则fX(x)和hX(x)对于fX(x)的交叉熵定义为2个概率密度函数比值对数的期望，即

(9)

式中：D(·,·)为交叉熵。

由式(9)可知：当fX(x)=hX(x)时，D(f,h)=0。设fX(x;θ)为基本输入随机变量的概率密度函数，其中θ为分布参数。根据重要抽样法相关结论，最优重要抽样密度函数为[21]

(10)

(11)

式(11)中，右端第一项为定值，因此最小化D(h*,h)等价于

maxE[IF(x)ln(hX(x;v))]

(12)

对于式(12)的最大化问题，通常情况下，没有解析解，因此需要采用随机抽样方法进行求解。使用直接蒙特卡罗方法，根据原分布fX(x;θ)，抽取N个随机样本(x1,x2,…,xN)，式(12)可以转化为

(13)

对于稀疏事件，仍然存在大部分示性函数IF(xi)=0的困难。因此，可以引入另一个重要抽样过程，其重要抽样密度函数为hX(x;w)，定义权函数为

(14)

式中：w为分布参数。

则式(12)转变为

maxE[IF(x)W(x)ln(fX(x;v))]

(15)

从重要抽样密度函数hX(x;w)中抽取N个随机样本点(x1,x2,…,xN)，则式(15)的随机对应问题变为

(16)

可以证明式(16)的优化问题关于v是凸且可微的，并且对于常用的正态分布、指数分布和威布尔分布等自然指数分布族，式(16)存在解析解。考虑一维正态分布，分布参数为(μ,σ)，式(16)与式(17)的最小化问题等价[21]：

(17)

很容易可以得出最小化问题的最优解为[21]

(18)

(19)

式中：Ii=IF(xi)。

可以将式(18)和式(19)直接拓展至多维随机正态向量的情况。然而当失效概率非常小时，应用以上结果仍然很困难，主要是因为大部分的随机样本还是落在失效域之外。因此Rubinstein[15-16]提出了多层交叉熵方法(Multi-Level Cross Entropy Method)。该方法是通过增加一个控制参数ρ——中间失效概率，产生中间失效事件，并使得中间失效事件逐渐向失效域靠近。由此构建交叉熵算法：

1) 初始化待定分布参数v0=θ，迭代计数j=0。

2) 从hX(x;vj)产生N个随机样本(x1,x2,…,xN)，计算功能函数值(g(xi))，并且对(g(xi))从小到大排序，得到(gi)，求得功能函数值次序统计量的ρ分位数bj=g[ρN]。

4) 若bj>0，设j=j+1，转步骤2)。

5) 基于最终的重要抽样密度函数，生成随机样本。

文献[14]所提方法通过交叉熵方法确定重要抽样密度函数之后，为求得所有输入随机变量的可靠性灵敏度指标，首先抽样两个N×n的样本矩阵A和B，然后构造矩阵Ci(i=1,2,…,n)，该矩阵为B的第i列被A的第i列替代后的矩阵，最后根据样本矩阵A、B、Ci(i=1,2,…,n)计算可靠性灵敏度指标，具体计算细节见文献[14]。使用该方法计算灵敏度指标的总的计算量为N(n+2)+Nce，其中，Nce为使用交叉熵方法确定抽样中心所需样本数。可以看出，文献[14]所提方法的计算量与问题的维数相关，模型维数增加，其计算量也随之增加。

2.2 基于交叉熵和空间分割的Si的近似计算

本节参考Zhai等在文献[17]中所提的基于方差的空间分割方法，给出基于失效概率的全局灵敏度指标的高效计算方法，该算法的计算量与问题维数无关。根据式(7)可知，可以通过计算E[E2(IF|Xi)]进而得到Si的估计值：

(20)

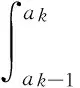
(21)

由式(21)可知，只需计算出Pk、E(IF|Xi∈Ak)和PfY，便可得到随机变量的可靠性灵敏度指标Si。其中Pk和PfY的计算前文已经提到，下面着重推导E(IF|Xi∈Ak)的计算：

(22)

至此，将式(22)代入式(21)中即可得到失效概率矩阵独立全局灵敏度指标。2.3节将给出本文所提方法的具体计算流程。

2.3 基于失效概率的全局灵敏度的计算流程

步骤1根据交叉熵方法确定重要抽样函数，具体实施过程见2.1节。

步骤2基于步骤1所得的重要抽样密度函数hX(x),抽样N×n的样本矩阵A。

(23)

步骤3根据失效域指示函数IF的定义，计算样本矩阵A对应的IF(x)；根据失效概率的定义，计算PfY:

(24)

步骤4将Xi的样本空间等样本数的连续的分为s个无重叠的子区间，Ak=[ak-1,ak),1≤k≤s

步骤5根据Ak，找到与之对应的样本输出IF的子集，即：Bk=(IF|Xi∈Ak)

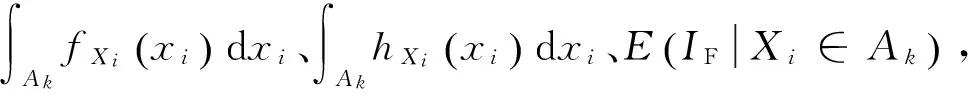
(25)

(26)

(27)

(28)

步骤7将式(28)代入式(21)中，可得Si的估计值。本文所提的基于交叉熵和空间分割计算全局灵敏度的方法，规避了常规重要抽样法中确定重要抽样函数的困难，并且仅需一组样本，便可计算出所有变量的灵敏度指标，计算量与问题维数无关，提高了计算效率。能够较好地解决多设计点问题和小失效概率问题。

2.4 空间分割策略

在空间分割方法中，采用何种划分方式将关系到计算结果的好坏[18-20]。文献[18]提出几种不同的分割方法，Plischke等[20]指出等样本数目划分是一种简单有效的方法，Li和Mahadevan在文献[19]也使用了这种分割方法，因此本文采用等样本数目划分的方式计算。

3 算例分析

本节通过1个数值算例和2个工程算例说明所提方法的合理性和高效性，并与蒙特卡罗法以及文献[14]所提方法的计算结果进行对比分析。为公平地比较每种方法的效率和精度，文中给出100次重复计算结果的方差和均值。

算例1考虑一个结构系统，其极限状态函数为

(29)

式中：Xi(i=1,2,3)～N(0,1)。将蒙特卡罗法计算所得结果，作为参照解。本文使用交叉熵方法确定抽样中心，单层样本量N0=1 000，初始参数ρ=0.07，在该算例中多层交叉熵的迭代次数仅为1次，使用1 000个样本点，用于确定重要抽样密度。根据交叉熵方法所得重要抽样密度函数，抽样1 000个随机样本，计算失效概率，基于评估失效概率所使用的这组样本，利用空间分割方法，计算变量的灵敏度指标。计算结果如表1和图1所示，表中Ncall为每次计算需要调用极限状态函数的次数。

从图1可以看出，文献[14]所提方法与本文所提方法计算结果均与参照解吻合较好，从而说明了文中所提方法的正确性；由表1中100次重复计算结果的方差容易看出，在方差相当的情况下，本文所提方法调用极限状态函数的次数明显小于文献[14],说明所提方法的样本利用率以及计算效率更高。这是因为本文方法只需重复利用产生的一组样本，即可得到所有变量的灵敏度指标，而文献[14]所提方法计算量与问题维数相关，为Ncall=N(n+2)+Nce。

由计算结果可知输入随机变量的重要度排序为X3>X2>X1，显然，若能设法减少输入随机变量X3的不确定性，可以有效地降低结构系统的失效概率。

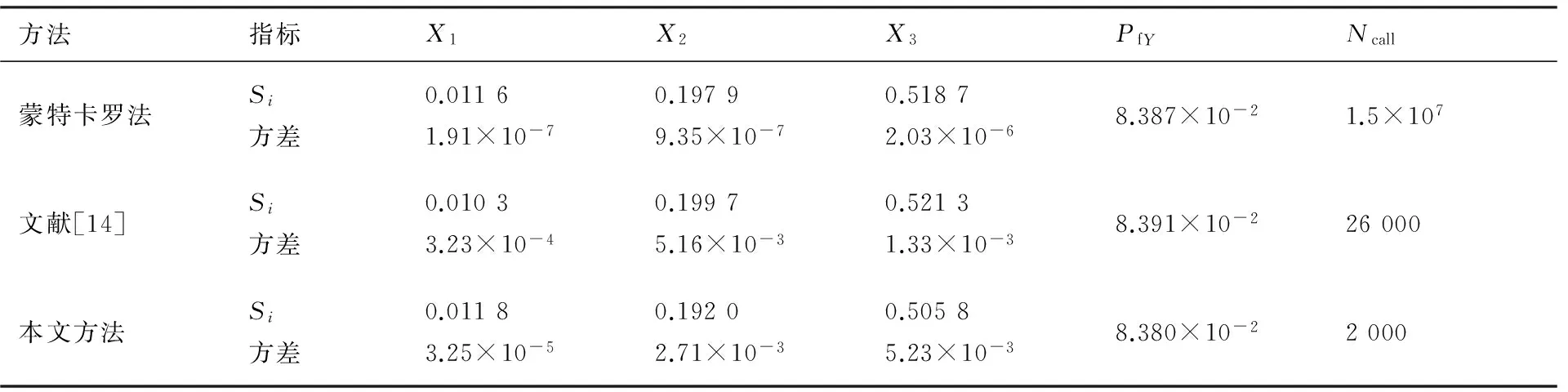
表1 算例1基于全局可靠性灵敏度计算结果Table 1 Results of global sensitivity analysis for Example 1

图1 算例1重要性测度结果Fig.1 Results of importance measure of Example 1

算例2考虑屋架问题

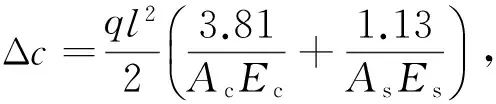
图2 屋架结构的简单示意图Fig.2 Schematic diagram of roof truss

本算例中，使用蒙特卡罗法的计算结果作为参照解，为方便对比，将表3的计算结果绘制成柱状图(图3)。由图3可以看出：本文方法与参照解吻合较好，从而说明其准确性。根据表3易得，与文献[14]方法相比，在稳健性相当的情况下，本文方法使用的样本数与问题维数无关，其计算效率更高。

由图3进一步可知：本文所提方法得到的输入变量的重要性排序与蒙特卡罗方法所得排序一致，均为：Ac>q>Es>As>l>Ec。可以看出，混凝土的截面积Ac的重要度较之其他变量大许多，因此降低Ac的不确定性可以最大程度地改善结构的可靠性。

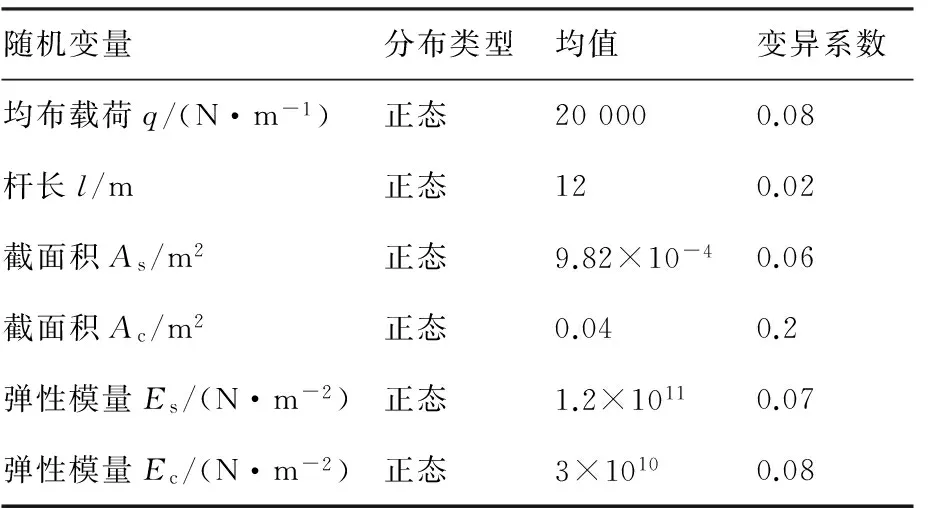
表2 屋架结构的随机变量的分布参数

表3 屋架结构的全局可靠性灵敏度计算结果Table 3 Results of global sensitivity analysis for roof truss

图3 屋架结构重要性测度结果Fig.3 Results of importance measure of roof truss

算例3三盒段机翼结构

该算例修改自文献[22]。翼盒是飞机结构的重要组成部件，支撑着机翼的主要框架。如图 4所示的三盒段机翼结构，由16个板和28个杆组成。结构中28个杆由不同方向区分成3类，即x、y和z方向。在每一个方向上的杆的长度和横截面积均相同。L1、L2、L3分别表示x、y、z这3个方向上杆的长度；所有杆的横截面积均为A；杆和板的弹性模量为E;泊松比为0.3；P为施加在节点上的外载荷;T为板的厚度。

假设各个输入随机变量之间相互独立，且均服从正态分布，具体的分布参数见表4。

图4 翼盒结构示意图Fig.4 Diagram of wing box structure

表4 翼盒结构随机变量的数字特征

Table 4 Parameters of random variables of wing box

structure

随机变量均值变异系数标准差L1/m0.60.050.03L2/m0.20.050.01L3/m0.40.050.02A/m20.00010.10.00001T/m0.0030.10.0003E/Pa7.1×10100.17.1×109P/N15000.1150

盒段的设计目标之一是在外载荷的作用下，位移不能超过某一个值。根据这一准则，极限状态函数可以构建为

g(x)=Dt-d(L1,L2,L3,A,T,E,P)

(30)

式中：Dt=0.006 m为最大允许位移，d(L1,L2,L3,A,T,E,P)为三盒段机翼结构的最大位移，可以通过有限元分析计算得到。在ANSYS中建立三盒段机翼的有限元模型，如图5所示。

采用交叉熵方法，设定初始参数ρ=0.07，单层样本量N0=1 000。该算例计算过程中，多层交叉熵的迭代次数仅为2次，使用2 000个样本点。确定抽样中心后，重要抽样1 000个样本点，应用空间分割法，计算输入变量的可靠性灵敏度指标。使用蒙特卡罗法，文献[14]所提方法和本文所提方法可靠性灵敏度指标的计算结果见表5。

以蒙特卡罗法的计算结果作为参照解，从图6中可以看出，3种方法的结果吻合很好。无论是重要度排序还是数值结果，本文所提方法与蒙特卡罗法均一致。由表5中100次重复计算结果的方差可知：与文献[14]相比，在方差相当的前提下，本文方法使用的样本数目更少，其计算效率更高。从计算结果可以看出，输入变量的重要度排序为：E>L2>P>T>A>L1>L3，其中变量E和L2对模型输出不确定性有比较大的影响。因此，在设计过程中，工程设计人员可以通过控制上述重要变量的不确定性来高效的提高机翼翼盒的可靠性。

图5 翼盒结构有限元模型Fig.5 Finite element model of wing box structure

表5 翼盒结构全局可靠性灵敏度计算结果Table 5 Results of global sensitivity analysis for wing box structure

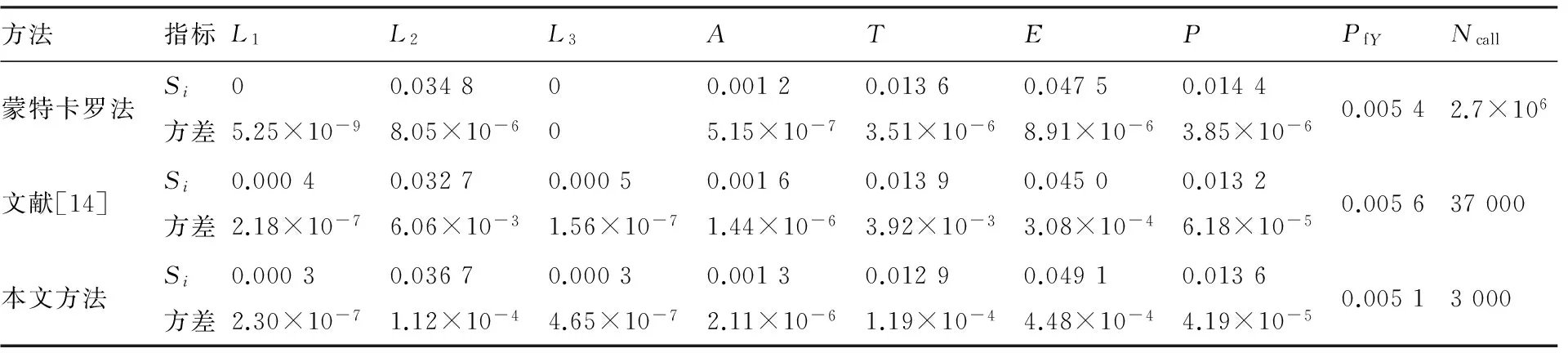
方法指标L1L2L3ATEPPfYNcall蒙特卡罗法Si方差05.25×10-90.03488.05×10-6000.00125.15×10-70.01363.51×10-60.04758.91×10-60.01443.85×10-60.00542.7×106文献[14]Si方差0.00042.18×10-70.03276.06×10-30.00051.56×10-70.00161.44×10-60.01393.92×10-30.04503.08×10-40.01326.18×10-50.005637000本文方法Si方差0.00032.30×10-70.03671.12×10-40.00034.65×10-70.00132.11×10-60.01291.19×10-40.04914.48×10-40.01364.19×10-50.00513000

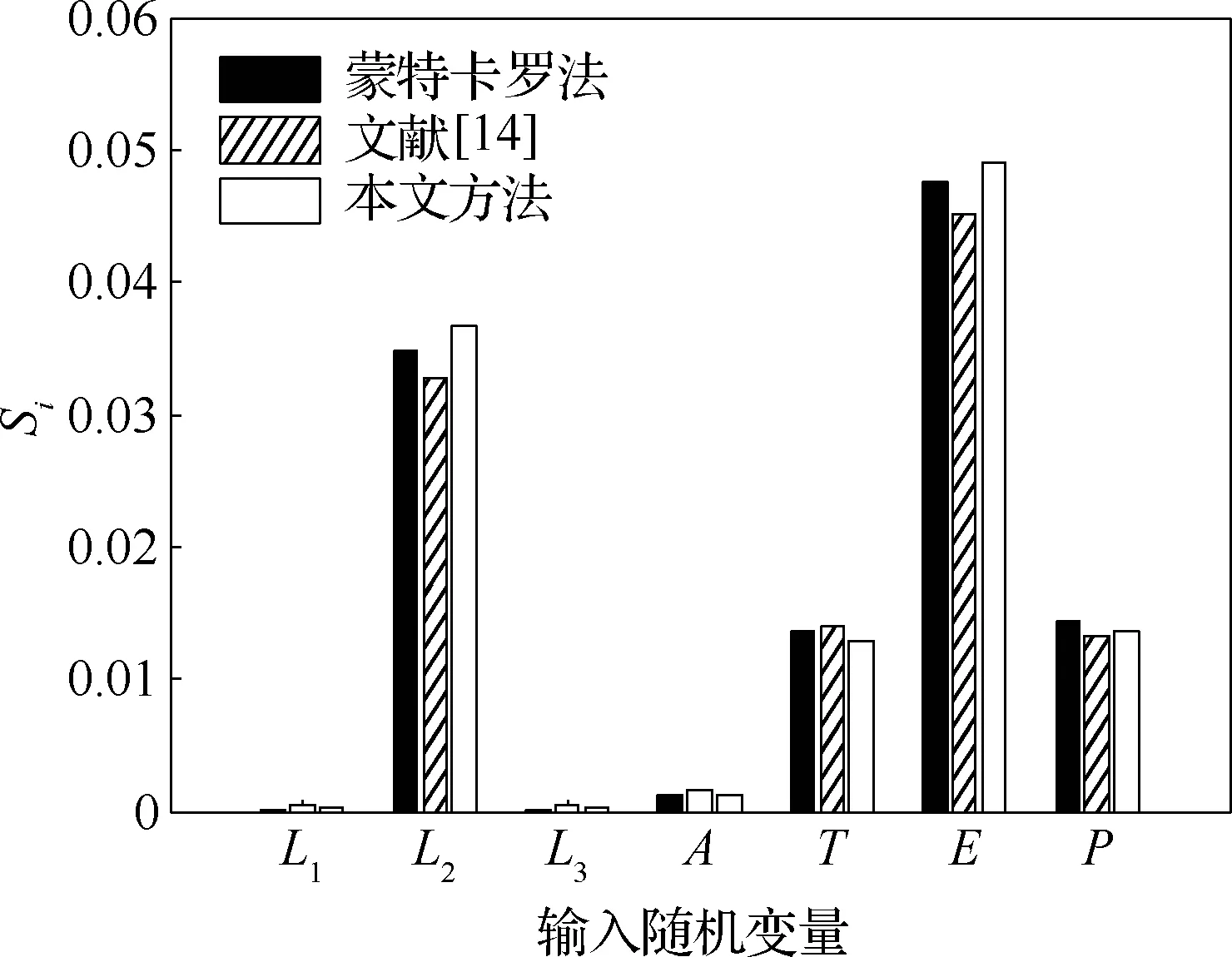
图6 翼盒结构重要性测度结果Fig.6 Results of histogram of importance measure of wing box structure

4 结 论

基于失效概率的全局灵敏度分析，本文提出了基于交叉熵和空间分割的的高效算法。交叉熵算法自适应移动抽样中心，逐步确定重要抽样密度函数，适用于非线性极限状态函数和多设计点的复杂情况。使用这种方法可以使得更多的样本点落入失效域，提高抽样效率。在此基础上，使用空间分割方法，重复利用一组样本，通过对这组样本的不同划分即可得到所有变量的灵敏度指标，极大地提高了样本的利用效率，降低了计算量。本文通过3个算例，验证了所提方法的计算效率和精度，为工程全局可靠性灵敏度分析提供了新工具。

[1] SALTELLI A. Sensitivity analysis for importance assessment[M]. New Dersey: Wiley, 2002: 579-590.

[2] 吕震宙, 宋述芳， 李洪双, 等. 结构机构可靠性及可靠性灵敏度分析[M]. 北京： 科学出版社, 2009: 6-8.

LU Z Z, SONG S F, LI H S, et al. Reliability and sensitivity analysis of structure and mechanism[M]. Beijing: Science Press, 2009: 6-8 (in Chinese).

[3] SALTELLI A. Global sensitivity analysis: The primer[M]. New Dersey: Wiley, 2004: 1-42.

[4] HELTON J C, DAVIS F J. Latin hypercube sampling and the propagation of uncertainty in analyses of complex systems[J]. Reliability Engineering & System Safety, 2003, 81(1): 23-69.

[5] SALTELLI A, MARIVOET J. Non-parametric statistics in sensitivity analysis for model output: A comparison of selected techniques[J]. Reliability Engineering & System Safety, 1990, 28(2): 229-253.

[6] IMAN R L, HORA S C. A robust measure of uncertainty importance for use in fault tree system analysis[J]. Risk Analysis, 1990, 10(3): 401-406.

[7] SOBOL I M. Global sensitivity indices for nonlinear mathematical models and their Monte Carlo estimates[J]. Mathematics & Computers in Simulation, 2001, 55(1-3): 271-280.

[8] BORGONOVO E. A new uncertainty importance measure[J]. Reliability Engineering & System Safety, 2007, 92(6): 771-784.

[9] 吕震宙, 李璐祎, 宋述芳, 等. 不确定性结构系统的重要性分析理论与求解方法[M]. 北京： 科学出版社, 2015: 1-8.

LU Z Z, LI L Y, SONG S F, et al. The important analysis theory and the solution method of the uncertainty structure system[M]. Beijing: Science Press,2015:1-8 (in Chinese).

[10] CUI L J, LU Z Z, ZHAO X P. Moment-independent importance measure of basic random variable and its probability density evolution solution[J]. Science China Technological Sciences, 2010, 53(4): 1138-1145.

[11] LI L, LU Z Z, FENG J, et al. Moment-independent importance measure of basic variable and its state dependent parameter solution[J]. Structural Safety, 2012, 38(38): 40-47.

[12] BORGONOVO E, CASTAINGS W, TARANTOLA S. Model emulation and moment-independent sensitivity analysis: An application to environmental modelling[J]. Environmental Modelling & Software, 2012, 34(8): 105-115.

[13] WEI P F, LU Z Z, HAO W R, et al. Efficient sampling methods for global reliability sensitivity analysis[J]. Computer Physics Communications, 2012, 183(8): 1728-1743.

[14] 任超， 李洪双. 基于失效概率的全局重要性测度分析的交叉熵方法[J]. 西北工业大学学报， 2017， 35(3): 536-544.

REN C, LI H S. Cross-entropy method for failure probability based global importance measure analysis[J]. Northwestern Polytechnical University, 2017， 35(3): 536-544 (in Chinese).

[15] RUBINSTEIN R Y. Optimization of computer simulation models with rare events[J]. European Journal of Operational Research, 1997, 99(1): 89-112.

[16] RUBINSTEIN R Y. The cross-entropy method for combinatorial and continuous optimization[J]. Methodology & Computing in Applied Probability, 1999, 1(2): 127-190.

[17] ZHAI Q, YANG J, ZHAO Y. Space-partition method for the variance-based sensitivity analysis: Optimal partition scheme and comparative study[J]. Reliability Engineering & System Safety, 2014, 131(6): 66-82.

[18] PLISCHKE E. An adaptive correlation ratio method using the cumulative sum of the reordered output[J]. Reliability Engineering & System Safety, 2012, 107: 149-156.

[19] LI C, MAHADEVAN S. An efficient modularized sample-based method to estimate the first-order Sobol’ index[J]. Reliability Engineering & System Safety, 2016, 153: 110-121.

[20] PLISCHKE E, BORGONOVO E, SMITH C L. Global sensitivity measures from given data[J]. European Journal of Operational Research, 2013, 226(3): 536-550.

[21] 李洪双, 马远卓. 结构可靠性分析与随机优化设计的统一方法[M]. 北京： 国防工业出版社, 2015: 129-139.

LI H S, MA Y Z. Unified methods for structure reliability analysis and stochastic optimization design [M]. Beijing: National Defense Industry Press, 2015: 129-139 (in Chinese).

[22] ZHOU C, LU Z, YUAN X. Use of relevance vector machine in structural reliability analysis[J]. Journal of Aircraft, 2013, 50(6): 1726-1733.