基于确定可能性均值法求解模糊随机双层规划问题
任 爱 红
( 宝鸡文理学院 数学与信息科学学院, 陕西 宝鸡 721013 )
0 引 言
双层规划问题(bilevel programming problem,BLPP)是一类具有主从递阶结构的复杂决策问题,已被广泛应用于经济管理、网络规划、供应链管理、工程问题等实际领域[1-4].双层规划的NP-hard性以及非凸不可微性,使得求解此类问题异常复杂,目前对双层规划的研究仍以所有系数均为实数的确定型双层规划为主.然而,在许多实际两层递阶决策问题中,经常存在着各种不确定性,如模糊不确定性和随机不确定性等,显然确定型双层规划无法完全反映这些不确定性现象,在使用上存在一定程度的局限性,因此将各种不确定性现象考虑到双层规划问题中的研究将具有重要的实际意义.
基于模糊规划和随机规划这两类不确定性优化方法,模糊双层规划和随机双层规划模型被相继提出.尽管这两种不确定型双层规划模型能分别从模糊不确定性和随机不确定性的角度描述不确定两层递阶决策问题,但难以全面刻画同时含模糊性和随机性的双重不确定性环境下的实际递阶决策过程,因此需进一步深入研究包含模糊随机不确定性的双层规划.模糊随机变量是描述模糊随机双重不确定性现象的一种数学工具.近年来,一些学者将模糊随机变量这一数学概念引入到双层规划问题中,开展了对模糊随机不确定性环境下双层规划问题的研究.相比模糊或随机双层规划,由于双重不确定性的复杂性和双层规划自身求解困难的特性,模糊随机双层规划问题更加难以处理.
目前关于求解模糊随机双层规划的研究大多集中在上下层目标函数中含模糊随机变量系数和约束函数中是实系数的情形.例如,Sakawa等[5]在上下层决策者非合作的情况下,采用Fractile模型以及可能性和必然性测度将模糊随机双层规划变形为一个确定双层线性分数规划,通过结合变量变形法和K次最好算法求得问题的一个Stackelberg解.针对同样的问题,Ren等[6]基于区间规划方法和期望优化模型将原问题转化为一个确定多目标双层规划模型,并设计了求解偏好最优解的两个算法.随后,Sakawa等[7]利用可能性和必然性测度以及绝对偏差最小化方法来处理模糊随机双层规划问题.然而,针对求解上下层目标函数和约束函数均含有模糊随机变量系数的双层情形,当前研究成果还非常少.Ren等[8]结合最优值区间方法、期望模型以及概率机会约束条件讨论了此类模糊随机双层规划的最优值问题.
本文针对所有系数均为模糊随机变量的模糊随机双层规划模型,引入模糊随机变量的期望值、模糊数的确定可能性均值和模糊机会约束条件处理原问题的随机性和模糊性,建立模糊随机双层确定可能性均值-机会约束规划模型,给出其确定等价双层线性模型,并利用K次最好算法进行求解.最后以数值例子证明所提方法的可行性.
1 理论基础
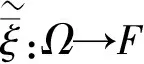

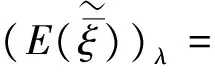

其中函数L,R:[0,)→[0,1]是单调不增函数,且满足L(0)=R(0)=1,ξ(ω)是模糊随机变量的中心值,αξ,βξ>0分别为左宽度和右宽度.LR型模糊随机变量可表示为∀ω∈Ω.本文假设ξ是服从均值为E(ξ)和方差为的正态分布的随机变量,记为




2 基于确定可能性均值和机会约束规划的求解方法
2.1 问题形式
考虑上下层目标函数和约束函数中同时含模糊随机变量系数的模糊随机双层线性规划问题,其数学模型表示为

x2是下面问题的解:

k=1,2,…,m,
x1=(x11x12…x1n1)T≥0,
x2=(x21x22…x2n2)T≥0
(1)
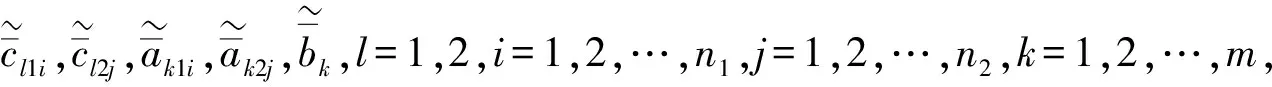
由于模型(1)中系数均为模糊随机变量,运用扩展原则,可知上下层目标函数以及每个约束函数的左侧都是模糊随机变量,因此该问题不是一个严格的数学规划模型.为解决此类问题,本文融合模糊随机变量的期望值、模糊数的确定可能性均值和基于可能性测度的模糊机会约束条件处理模型中的双重不确定性,由此构建模糊随机双层确定可能性均值-机会约束规划模型,再给出其确定等价模型进行求解.
2.2 模糊随机双层确定可能性均值-机会约束规划模型
模糊随机变量的期望值是模糊随机变量最重要的数字特征之一,它刻画了模糊随机变量向其均值靠拢的趋向值,是一种最常用的去随机化方法.当决策者希望在期望约束下优化上下层目标函数的平均值,则模型(1)中所有约束函数的左右两侧以及上下层目标函数就可以用其相应的期望值来代替,可得如下形式的模型:

x2是下面问题的解:

k=1,2,…,m,
x1=(x11x12…x1n1)T≥0,
x2=(x21x22…x2n2)T≥0
(2)
模糊随机变量的期望值本质上是一个模糊数,故模型(2)中每一个约束都是模糊约束,上下层目标函数也全是模糊数,因此该模型便是一个模糊双层规划模型.
由于模糊约束不可能给出一个确定的约束域,若希望模糊约束能以一定的置信水平成立,则可采用模糊机会约束条件.基于可能性测度,模型(2)中第k个模糊约束可转化为如下模糊机会约束条件:
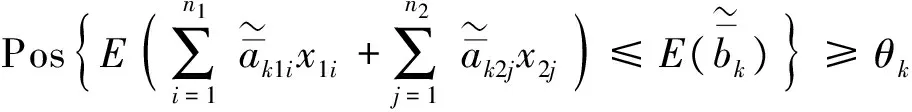
k=1,2,…,m
其中θk∈[0,1]表示决策者事先给定的置信水平.
对于模型(2)中上下层目标函数,需引入模糊数之间的排序方法对不同决策变量下模糊目标函数值进行比较.本文利用Carlsson等[10]提出的模糊数确定可能性均值概念清晰反映模型(2)中上下层目标函数的期望值,并对模糊目标函数值进行比较.基于这一概念,模型(2)中上下层目标函数的确定可能性均值为
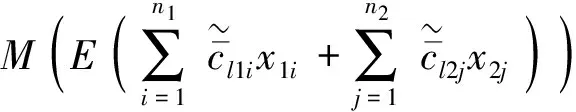
基于上面的讨论,建立如下形式的模糊随机双层确定可能性均值-机会约束规划模型:
x2是下面问题的解:

x1=(x11x12…x1n1)T≥0,
x2=(x21x22…x2n2)T≥0
(3)
对给定的θk(k=1,2,…,m),令模型(3)的约束域为

接下来,引入模糊随机双层规划问题(1)的M-POS-最优解概念.


则称x2为模型(1)下层规划的M-POS-最优解.
对给定的x1≥0,记M(x1;θk)表示模型(1)下层规划的M-POS-最优解集.
在给定置信水平θk(k=1,2,…,m)下,定义模型(1)的M-POS-可行域为
IR(θk)={(x1,x2)|(x1,x2)∈S(θk),
x2∈M(x1;θk)}

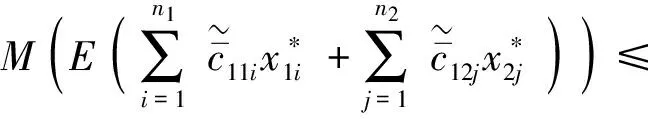



由定理1可知,为获得模糊随机双层规划问题(1)的M-POS-最优解只需求得模糊随机双层确定可能性均值-机会约束规划模型(3)的最优解.本文假设模型中不确定系数均为LR型模糊随机变量,下面给出模型(3)的确定等价形式.
2.3 确定等价形式
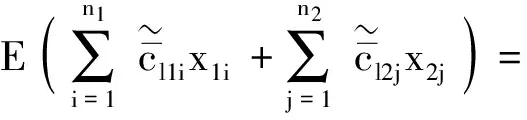
且λ-水平集为



相似地,模型(1)中每个约束函数的左侧也都是LR型模糊随机变量,相应的期望值也是LR型模糊数,表示为

根据引理1,模型(3)中约束条件
等价于

根据以上结果,模型(3)变形为如下确定双层线性规划问题:

x2是下面问题的解:
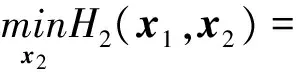


x1=(x11x12…x1n1)T≥0,
x2=(x21x22…x2n2)T≥0
(4)
特别地,当L(x)=R(x)=1-x(x∈[0,1])时,则LR型模糊随机变量系数退化为三角模糊随机变量.因此模型(4)可写为

x2是下面问题的解:
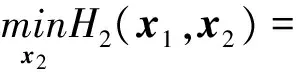
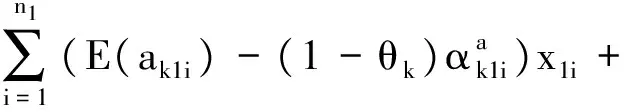

x1=(x11x12…x1n1)T≥0,
x2=(x21x22…x2n2)T≥0
(5)
双层线性规划问题至少有一个全局最优解在其约束域的极点处达到.基于这一重要性质,本文利用K次最好算法[12]来求解模型(4)和(5).这类方法的基本思想是首先在约束域上求解上层规划获得最优解,再检验该解是否也是下层规划的最优解.若是,则这个解便是双层线性规划问题的最优解;否则,从这个解的相邻顶点组成的待检验顶点集合中寻找使上层规划达到最优的点,同时检验这个顶点是否是下层规划的最优解.重复以上过程,直到在约束域中获得最优解.
3 数值例子及分析
例1[8]考虑如下模糊随机双层规划问题:

(x2,x3)是下面问题的解:

x1≥0,x2≥0,x3≥0
(6)
其中上下层目标函数以及约束函数中右侧系数都为三角模糊随机变量,具体数据如表1所示.


表1 例1中上下层目标函数和约束函数右侧系数Tab.1 Coefficients in the upper and lower level objective functions as well as the right hand side of each constraint function of example 1
根据模型(5),建立模型(6)的确定双层线性规划模型:

(x2,x3)是下面问题的解:
s.t.2x1+5x2+x3≤120.0+(1-θ1)×10.0,
5x1+3x2+2x3≤115.0+(1-θ2)×8.0,
x1+2x2+4x3≤100.0+(1-θ3)×5.0,
x1≥0,x2≥0,x3≥0
(7)

文献[8]融合α-水平集的最优值区间、期望模型和概率机会约束规划方法来求解例1.当α=0.6时,可得该例的最好Stackelberg解和最差Stackelberg解分别为(14.4,0,21.5)和(13.4,0,20.7).根据模型(7),这两个解相应的上层目标函数值分别为-186.6和-177.8,下层目标函数值分别为-60.00和-59.16.显然,本文所提出的方法给出了更好的上层目标函数值;所得到的下层目标函数值好于最差Stackelberg解相应的目标值和略差于最好Stackelberg解相应的结果.考虑到上层决策者处于主导地位,更侧重于关心上层目标函数值,因此本文方法得到的下层目标函数值是可接受的.
注意到模型中含有参数θ1、θ2、θ3,由于不同决策者会有想要达到的不同置信水平,因此需分析不同的置信水平对最优解以及上下层目标函数最优值的影响.为了方便计算,以下令θ1=θ2=θ3=θ.表2给出了置信水平θ的灵敏度分析.
由表2可以看出,不同的置信水平产生了不同的最优解和不同的上下层目标函数值.当参数θ增大,上下层目标函数值H1和H2增大;反之随着参数θ减小,两个目标函数值减小.这是由于当参数θ取值较大时,问题的可行域将收缩,就会产生较差的目标函数值;反之θ取值较小时,问题的可行域将扩大,就会产生较好的目标函数值.此外,当参数θ取值较大时,破坏约束的风险将降低;反之θ取值较小时,破坏约束的风险将增大.


表2 例1中参数θ的灵敏度分析Tab.2 Sensitivity analysis of parameter θ of example 1
例2某一家电公司和其分公司生产4种厨房小家电,包括电压力锅、电磁炉、电烤箱和面包机.总公司处于决策主导地位,分公司处于决策从属地位,他们的目标都是最小化各自生产费用.令上层决策变量x1、x2是总公司生产电压力锅、电磁炉的数量,下层变量y1、y2是分公司生产电烤箱和面包机的数量.由于市场经济的随机变化和市场需求的模糊不确定性,总公司和分公司生产每一种家电的单位费用也是不确定的,既具有随机性又具有模糊性,可考虑这些值为模糊随机变量.此外,总公司和分公司的费用最小化需受到其原材料成本、人力成本、设备使用以及营销成本的限制,相关参数也应考虑为模糊随机变量.假定这些参数均是三角模糊随机变量.基于以上分析,这个生产决策问题可通过如下模糊随机双层规划模型表示:
(x3,x4)是下面问题的解:

x1≥0,x2≥0,x3≥0,x4≥0
(8)
其中模糊随机变量系数的具体值见表3.
令置信水平θ1=θ2=θ3=θ4=0.9.由模型(5),则问题(8)转化为如下确定双层线性规划问题:

(x3,x4)是下面问题的解:

s.t.(1.0-0.1×0.5)x1+(1.0-0.1×0.4)x2+(1.0-0.1×0.3)x3+(1.0-0.1×0.4)x4≤50.0+0.1×1.5,
(1.0-0.1×0.8)x1+(3.0-0.1×0.5)x2+(1.0-0.1×0.3)x3+(5.0-0.1×0.4)x4≤80.0+0.1×1.5,
(1.0-0.1×0.6)x1+(4.0-0.1×0.5)x2+(2.0-0.1×0.4)x3+(4.0-0.1×0.8)x4≤100.0+0.1×1.5,
(2.0-0.1×0.2)x1+(2.0-0.1×0.8)x2+(6.0-0.1×0.6)x3+(3.0-0.1×0.4)x4≤120.0+0.1×1.0,
x1≥0,x2≥0,x3≥0,x4≥0


表3 例2模糊随机变量系数Tab.3 Coefficients of fuzzy random variables of example 2

接下来令θ1=θ2=θ3=θ4=θ.现将置信水平分别设置为0.5、0.6、0.7、0.8和0.9,计算结果如表4所示.由表4可以看出,当θ=0.5时,获得最好的上下层目标函数值分别为-149.382 0和-108.854 7;当θ=0.9时,获得最差的上下层目标函数值分别为-129.285 8和-85.458 4.事实上,随着置信水平降低,相应的确定性约束范围变宽,更易产生更好的上下层目标函数最优值;反之当置信水平提高,确定性约束范围变窄,这将导致


表4 例2中参数θ的灵敏度分析Tab.4 Sensitivity analysis of parameter θ of example 2
更差的优化结果.事实上,当置信水平较低时,即决策者提高了不满足约束条件的风险水平,这将有利于获得更好的上下层目标函数值.因此在实际的决策中,决策者可以根据自己的风险态度来选择置信水平.例如,保守的决策者可以取较大的置信水平.
4 结 语
本文讨论了一类上下层目标函数和约束函数中系数都是模糊随机变量的双层规划问题.通过结合模糊随机变量期望值、模糊数的确定可能性均值和模糊机会约束规划方法,提出模糊随机双层确定可能性均值-机会约束规划模型,给出确定双层线性规划,并利用K次最好算法进行求解.如何推广本文提出的方法来求解模糊随机多层规划问题是下一步待研究的问题.
[1] KOZANIDIS G, KOSTARELOU E, ANDRIANESIS P,etal. Mixed integer parametric bilevel programming for optimal strategic bidding of energy producers in day-ahead electricity markets with indivisibilities [J].Optimization, 2013,62(8):1045-1068.
[2]FONTAINE P, MINNER S. Benders decomposition for discrete-continuous linear bilevel problems with application to traffic network design [J].TransportationResearchPartB:Methodological, 2014,70:163-172.
[3]WANG Danping, DU Gang, JIAO R J,etal. A Stackelberg game theoretic model for optimizing product family architecting with supply chain consideration [J].InternationalJournalofProductionEconomics, 2016,172:1-18.
[4]KALASHNIKOV V, MATIS T I, CAMACHO-VALLEJO J F,etal. Bilevel programming, equilibrium, and combinatorial problems with applications to engineering [J].MathematicalProblemsinEngineering, 2015,2015:490758.
[5]SAKAWA M, MATSUI T. Fuzzy random non-cooperative two-level linear programming through fractile models with possibility and necessity [J].EngineeringOptimization, 2013,45(7):811-833.
[6]REN Aihong, WANG Yuping. An interval approach based on expectation optimization for fuzzy random bilevel linear programming problems [J].JournaloftheOperationalResearchSociety, 2015,66(12): 2075-2085.
[7]SAKAWA M, MATSUI T. Bilevel linear programming with fuzzy random variables through absolute deviation minimization [J].InternationalJournalofOperationalResearch, 2016,25(1):1-27.
[8]REN Aihong, WANG Yuping. An interval programming approach for bilevel linear programming problem with fuzzy random coefficients [C] //2013IEEECongressonEvolutionaryComputation,CEC2013. Washington D C: IEEE Computer Society, 2013:462-469.
[9]PURI M L, RALESCU D A. Fuzzy random variables [J].JournalofMathematicalAnalysisandApplications, 1986,114(2):409-422.
[10]CARLSSON C, FULLÉR R. On possibilistic mean value and variance of fuzzy numbers [J].FuzzySetsandSystems, 2001,122(2):315-326.
[11]LI Jun, XU Jiuping, GEN M. A class of multiobjective linear programming model with fuzzy random coefficients [J].MathematicalandComputerModelling, 2006,44(11/12):1097-1113.
[12]BIALAS W F, KARWAN M H. Two-level linear programming [J].ManagementScience, 1984,30(8):1004-1020.

