时滞切换不确定神经网络系统的指数稳定性*

薛焕斌 张继业

(1.韩山师范学院数学与统计学院, 潮州 521041) (2.西南交通大学牵引动力国家重点实验室, 成都 610031)

引言

细胞神经网络是由Chua和Yang在1988年提出的[1,2]. 此后的20多年里,细胞神经网络得到了广泛的研究, 并成功应用于信号处理、模式识别、移动图像重构和解非线性代数方程等[2-5]. 这些应用依赖于神经网络平衡点的存在性和稳定性[6-8]. 不管是生物还是人工神经网络, 神经元之间的相互作用一般是不同步的, 特别在网络的硬件实现中, 由于信号传输速度的有限性, 使网络系统中的时间滞后不可避免. 另一方面, 在神经网络中引入时间滞后参量后, 有利于移动目标的图像处理, 移动物体速度的确定和模式分类[9]. 但时间滞后量的引入, 可能使网络产生振荡和不稳定性. 而且在大多数情况下, 时间滞后量是难以精确测量的, 并且随着时间的改变不断变化, 事实上是无界的. 也就是说, 过去的所有时刻影响着现在的状态[10]. 再者, 由于外界扰动, 测量和建模误差等的存在, 神经网络模型一定含有影响其动力学行为的不确定性因素. 为了分析神经网络模型的鲁棒性, 一种合理的方法是假定参数属于已知的区间[11]. 因此, 对时滞区间神经网络模型的鲁棒稳定性研究具有理论和现实的重要性.

切换系统是一种混杂系统, 它由一系列的子系统和一个控制子系统之间切换规律的控制率组成. 最近, 切换系统受到越来越多的关注. 因为实际中很多系统(如生物系统,计算机控制系统, 工程系统等)都可以表述成切换系统. 另外, 从控制方面看, 多控制器的切换控制往往可以对复杂系统的控制起到满意的控制效果. 切换时滞系统作为一种新的复杂系统, 具有重要的理论研究意义. 由于连续和离散的动力学特征, 以及时间滞后之间的相互作用, 使得切换时滞系统的行为比一般的切换或时滞系统行为都要复杂得多. 切换时滞神经网络系统作为一种特殊的切换时滞系统也受到了越来越多的重视. 文献[12,13]运用线性矩阵不等式研究了时滞切换Hopfield神经网络的稳定性. Wu等利用平均驻留时间方法和自由权矩阵方法分析了时滞切换神经网络的指数稳定性[14]. Arunkumar等利用平均驻留时间方法和多Lyapunov函数法研究了一类离散切换神经网络的鲁棒稳定性[15].

正如前面提到的, 切换神经网络每个子系统平衡点的存在性, 唯一性和稳定性是非常重要的. 然而, 在现有的结论中, 很少结论跟子系统平衡点的存在性, 唯一性和稳定性直接相关. 而且大部分结论都是运用线性矩阵不等式方法, 但这种方法在实际工程应用上存在着诸多困难. 因为应用线性矩阵不等式方法必须人为的决定很多不确定参数和矩阵.

基于以上分析, 本文的主要目的是建立时滞切换UCNNs系统鲁棒指数稳定性的新条件. 运用Lyapunov泛函方法, 得到了时滞切换UCNNs系统 鲁棒指数稳定性的充分条件. 和前面的结论相比较, 本文的主要优点有: (a)系统的稳定性对参数摄动和切换信号扰动都具有鲁棒性; (b)得到的结论是显式结构, 有利于实际工程应用.

符号说明:x=(x1,x2,…,xn)T表示n维列向量(符号(·)T表示转置),Rn表示n维实数空间, |x|表示|x|=(|x1|,|x2|,…,|xn|)T, ‖·‖表示Euclidean范数; 对于矩阵A=(aij)n×n, |A|表示|A|=(|aij|)n×n;C((-∞,0];Rn)表示从(-∞,0]映射到Rn上的连续函数集.

1 预备知识

具有无穷时滞的UCNNs系统可以由以下时滞微分方程描述:

(1)

系统(1)的初始条件假设为ui(s)=φi(s),s∈(-∞,0], 其中φi∈C((-∞,0],R),i=1,2,…,n.

我们假设UCNNs系统(1)的激活函数满足如下条件:

假设1对于任意给定的ui,vi∈R,i∈{1,2,…,n},存在常数Li>0, 使得:

|gi(ui)-gi(vi)|≤Li|ui-vi|

即gi:R→R是全局Lipschitz.

在这种情况下, 我们称g(u)属于G类函数, 记为g(u)∈G. 并且记L=diag{L1,L2,…,Ln}.

时滞切换UCNNs系统是由一系列的时滞UCNNs系统和切换率组成的. 每个时滞UCNNs 系统视为子系统, 切换率决定了各个子系统之间的切换. 根据系统(1), 时滞切换UCNNs系统可以表示成如下形式:

(2)

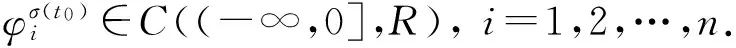
在本文中假定切换率σ(t)事先未知. 对应切换信号σ(t), 我们可以得到一个切换序列{(t0,i0),…, (tk,ik),…|ik∈Σ,k=0,1,…}, 这表示当时t∈[tk,tk+1), 第ik个子系统被激活.

定义指示函数:

γ(t)=(γ1(t),γ2(t),…,γN(t))T

其中:

k=1,2,…,N. 因此,时滞切换UCNNs系统(2)亦可表达成如下形式:

(3)

定义1如果对每个Ek∈EkI,Ak∈AkI,Bk∈BkI和输入Jk, 存在常数λ>0和η>0, 使得对所有的t≥t0都有:

‖u(t)-u*‖≤η‖φσ(t0)-u*‖e-λ(t-t0)

则称时滞切换UCNNs系统(3)的平衡点u*是鲁棒指数稳定的.

其中:

‖φσ(t0)-u*‖

2 时滞UCNNs系统平衡点的定性分析

本节我们将研究系统(1)平衡点的存在性, 唯一性和稳定性.

定义2对于实矩阵A=(aij)n×n, 如果aij≤0,i,j=1,2,…,n,i≠j, 且A的所有顺序主子式为正, 则称矩阵A为M-矩阵.

引理1[16,17]对于实矩阵A=(aij)n×n,如果aij≤0,i,j=1,2,…,n,i≠j, 则以下陈述等价:

(i)矩阵A为M-矩阵;

(ii)存在向量ξ>0, 使得ξTA>0.

定义3映射H:Rn→Rn为Rn上的同胚映射, 如果H∈C0是Rn上的单射和满射, 且H-1∈C0.

引理2[16]如果H(u)∈C0满足以下条件:

(i)H(u)是Rn上的单射;

则H(u)是Rn上的同胚映射.

证明: 定义如下与系统(1)相关的非线性映射:

H(u)=-Eu+(A+B)g(u)+I

如果H(u)为Rn上的同胚映射, 那么系统(1)存在唯一的平衡点u*[18]. 类似文献[8]定理1的证明, 容易得知H(u)满足引理2的两个条件. 因此, 对任意输入I, 映射H(u)为Rn上的同胚映射. 所以系统(1)存在唯一的平衡点u*. 记λ=E-(|A|+|B|)L, 因为π是M-矩阵, 由引理1知道, 存在ξi>0(i=1,2,…,n), 使得:

所以:

由引理条件(ii)可得, 矩阵λ是M-矩阵.类似文献[6]定理4的证明, 容易证明u*是指数稳定的.证毕.

3 时滞切换UCNNs系统的全局指数稳定性

本节将利用Lyapunov泛函方法, 研究时滞切换UCNNs系统(3)的全局指数稳定性.

定理2如果对任意的k∈Σ,gk∈G, 并存在一个n维正向量ξ=(ξ1,ξ2,…,ξn)使得:

(4)

其中:

那么对所有的Ek∈EkI,Ak∈AkI,Bk∈BkI和每个输入Jk, 系统(3)在任意切换信号下是鲁棒指数稳定.

(5)

其中:

考虑Lyapunov泛函:

(6)

其中ε>0待定. 计算V沿系统(5)的右上导数V+可得:

D+V(x,t)

(7)

定义函数:

由不等式(4)知道:

所以:

V(x,t)≤V(x,t0)

(8)

又因为当t=t0时,第i0个子系统被激活,所以:

V(x,t0)

由积分中值定理知道, 存在ρ>0使得:

V(x,t0)

(9)

其中:

结合(6)～(9)式可得:

令ξ=min1≤i≤nξi可得:

由定义1知道,系统(3)的平衡点u*是鲁棒指数稳定的. 证毕.

注2我们知道, 在任意切换的条件下得到的稳定条件可能具有较强的保守性. 但是这样的条件能确保系统的稳定性对切换信号具有鲁棒性. 由于网络系统相互依赖的动力学特征, 使得切换信号往往是无法确定的. 因此, 系统的稳定性对切换信号的鲁棒性显得十分必要.

4 算例

下面给出一个数值仿真算例. 考虑如下二阶时滞切换UCNNs系统:

(10)

其中:

σ(t):[0,+∞)→Σ={1,2}

g1(u) =g2(u)

=(0.5u1+0.5sinu1,0.5u2+0.5sinu2)T

显然,g1,g2满足假设1, 且L1=L2=I2(其中I2为2阶单位矩阵),

取ξ=(1,1), 经简单计算可知:

(i,j,k=1,2)

满足定理2的所有条件, 因此系统(10)在任意切换信号下是鲁棒指数稳定的.

图1 切换系统(10)中子系统1的状态曲线Fig.1 State responses of the subsystem 1 in the switched system (10)

图2 切换系统(10)中子系统2的状态曲线Fig.2 State responses of the subsystem 2 in the switched system (10)

图3 切换系统(10)的状态曲线Fig.3 State responses of the switched system (10)

5 结论

本文研究了具有无穷时滞切换不确定细胞神经网络系统在任意切换下的鲁棒指数稳定性. 利用同胚映射和M-矩阵理论研究了子系统平衡点的存在性, 唯一性和稳定性; 利用Lyapunov泛函方法研究时滞切换不确定细胞神经网络的鲁棒指数稳定性. 有别于现有的线性矩阵不等式相关结论, 本文得到的稳定性条件是代数显式结构, 有利于实际工程应用. 最后通过数值算例说明如何应用定理的条件, 同时也验证了结论的正确性.

1Chua L O, Yang L. Cellular neural networks:theory.IEEETransactionsonCircuitsandSystems, 1988,35(10):1257～1272

2Chua L O, Yang L. Cellular neural networks:applications.IEEETransactionsonCircuitsandSystems, 1988,35(10):1273～1290

3Chua L O. CNN: A paradigm for complexity. Singapore: World Scientific, 1998

4Gupta M, Jin L, Homma N. Static and dynamic neural networks: from fundamentals to advanced theory. New York: Wiley, 2003

5Park J H, Kwon O M, Lee S M. LMI optimization approach on stability for delayed neural networks of neutral-type.AppliedMathematicsandComputation, 2008,196(1):236～244

6Zhang J. Absolutely exponential stability in delayed cellular neural networks.InternationalJournalofCircuitTheoryandApplications, 2002,30(4):395～409

7Zhang J, Suda Y, Iwasa T. Absolutely exponential stability of a class of neural networks with unbounded delay.NeuralNetworks, 2004,17(3):391～397

8Zhang J. Global exponential stability of interval neural networks with variable delays.AppliedMathematicsLetters, 2006,19(11):1222～1227

9Roska T, Chai W W, Balsi M, et al. Stability and dynamics of delay-type general and cellular neural networks.IEEETransactionsonCircuitsandSystemsI:FundamentalTheoryandApplications, 1992,39(6):487～490

10 刘铭,徐晓峰,张春蕊. 中立型时滞反馈扭转控制系统的稳定性分析. 动力学与控制学报, 2015,13(6):449～453 (Liu M, Xu X F, Zhang C R. Stability analysis of delayed torsional vibration system of neutral type.JournalofDynamicsandControl, 2015,13(6):449～453 (in Chinese))

11 Li N, Cao J. Switched exponential state estimation and robust stability for interval neural networks with the average dwell time.IMAJournalofMathematicalControlandInformation, 2015,32(2):257～276

12 Ahn C K. An H∞approach to stability analysis of switched Hopfield neural networks with time-delay.NonlinearDynamics, 2010,60(4):703～711

13 Lian J, Zhang K, Feng Z. Stability analysis for switched Hopfield neural networks with time delay.OptimalControlApplicationsandMethods, 2012,33(4):433～444

14 Wu L, Feng Z, Zheng W X. Exponential stability analysis for delayed neural networks with switching parameters: average dwell time approach.IEEETransactionsonNeuralNetworks, 2010,21(9):1396～1407

15 Arunkumar A, Sakthivel R, Mathiyalagan K, et al. Robust stability criteria for discrete-time switched neural networks with various activation functions.AppliedMathematicsandComputation, 2012,218(22):10803～10816

16 舒仲周,张继业,曹登庆. 运动稳定性. 北京:中国铁道出版社, 2001 (Shu Z Z, Zhang J Y, Chao D Q. Stability of Motion. Beijing: China Railway Publishing House, 2001 (in Chinese))

17 Siljak, D D. Large-scale dynamic systems: stability and structure. New York: North Holland, 1978

18 Forti M, Tesi A. New conditions for global stability of neural networks with application to linear and quadratic programming problems.IEEETransactionsonCircuitsandSystemsI:FundamentalTheoryandApplications, 1995,42(7):354～366