最小广义特征值在多元方差分析中的应用探讨

江忠伟

（中国人民银行南通市中心支行，江苏 南通 226007）

0 引言

多元方差分析是一元方差分析的推广，在选择检验统计量方面，通常的做法是：考虑到组内差异是由随机误差造成的，组间差异可能是由随机误差和系统误差共同引起的，与一元方差分析的基本思想相同。在一元方差分析中，若各个总体之间没有显著差异，则组间离差平方和与组内离差平方和近似相等。可以证明组间离差平和与组内离差平方和的比值服从F分布，给定显著性水平后，就可以算出临界值即得出拒绝域。与一元方差分析不同的是：多元统计分析需要将一元方差分析中的组间离差平方和、组内离差平方和推广为组间离差阵以及组内离差阵。然后基于组间离差阵与组内离差阵的比值构建检验统计量，可以证明该统计量为wilks统计量，给定显著性水平后，就可以算出临界值即得出拒绝域[1]。另外还有一些其他的检验统计量，例如Hotelling迹检验统计量[2,3]、Pil⁃lai-Bartlett准则检验统计量（Pillai-Bartlett criterion）[4,5]Roy最大特征值检验统计量（Roy’s Largest Root）[6]，具体表达形式见表1。

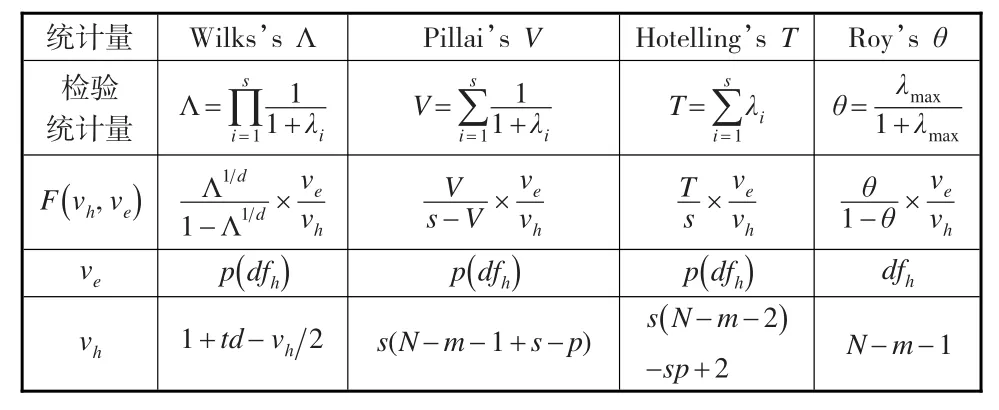
表1 四种检验统计量汇总

通过推导证明，四个检验统计量经过适当的变形均转化成服从F分布的检验统计量[7]。在进行多元方差分析时选择哪个检验统计量，是一个很有实际意义的问题。Stevens[7]对上述四个检验统计量拒绝原假设能力进行了比较，结果表明：在相同条件下，Roy最大特征值检验统计量拒绝能力最强。Olson[8]对上述四种检验统计量的检验稳健性进行了比较，结果表明：通常，Pillai-Bartlett准则检验统计量的稳健性好。

综上所述，四个检验统计量经过适当的变形均可以形成一个以F分布为渐近分布的随机变量，据此可以在给定的显著性水平下，设置一个小概率事件：当原假设成立时，检验统计量的取值落入构建的小概率事件中，则拒绝原假设。例如，利用wilks检验统计量进行检验的思路为：首先利用似然比原则导出服从wilks分布的检验统计量；由于对wilks检验统计量不够熟悉，通常将wilks检验统计量转换成F检验统计量；最后结合一个给定的显著性水平，就确定了拒绝域，即检验法则。其三个检验统计量也是按照这种思路：先利用样本资料导出一个统计量，再将该检验统计量转换成F检验统计量，最后结合一个给定的显著性水平确定拒绝域。有一个很自然的想法是：能否先对样本资料进行变换，然后再根据变换后的样本资料构建F检验统计量进行方差分析？

1 基本思路

多元方差分析的主要任务是检验因子的不同处理（类型变量）对不同处理下得到的样本观测值（数值变量）有无显著影响，即分类自变量对数值因变量有无显著影响。该模型可以表述为：设分类自变量有K个处理，可以将每个处理看成一个总体，则有总体：

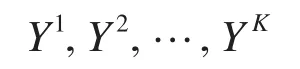
从这K个总体抽取如下样本：

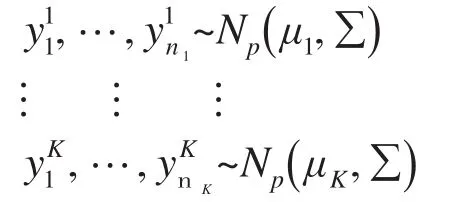
其中是相互独立的。

检验：

H0:至少有一组i≠j，使得μi≠μj，H1:μ1=…=μK，可以对m个总体中的所有样品做同一变换即选择一个p维行向量与所有的样品进行线性组合，显然：若H0:至少有一组i≠j，使得μi≠μj成立，则选取任意一个p维行向量，必有H0:至少有一组i≠j，使得≠成立；反之也是如此。

另一方面，由于服从p维多元正态分布的向量的分量的线性组合仍然服从正态分布，所以变换之后的样品数据仍然服从正态分布。据此可以构建F检验统计量进行一元方差分析。但F检验统计量的取值是无法确定的，虽然样本观测值是已知的，但p维行向量是未知的。如何求出？假设检验的目的是寻找证据支持本文的观点。通常的做法是设置两个对立事件，然后寻找一个特例拒绝与本文观点对立的观点，这样可以从一定置信水平上认为本文观点是正确的。因为拒绝一个观点只需要找到一个特例就行了，而接受一个观点需要考虑所有的情况（通常是做不到的），因此只需寻找特例来拒绝原假设。利用矩阵的谱分解以及向量的线性表出等知识，可以解出上述F检验统计量的最小值以及相对应l′的具体形式。如何利用这个极端值？一般的，对于假设检验中的原假设H0，可以认为H0是根据实际问题提出来的，往往是从过去经验中总结出来的，没有充分理由不能拒绝它。所以在多元方差分析中，当原假设为：H0:至少有一组i≠j，使得μi≠μj，若原假设为真，即各个总体的均值向量有显著差异，此时各水平的系统误差不为零，此时F检验统计量（为组间离差平方和与组内离差平方和的比值）会很大。但若由样本计算出的F检验统计量的值小到可以将其看成一个小概率事件，则可以认为原假设是不正确的，此时有较大把握拒绝原假设H0，接受备择假设H1。

2 依据样本资料直接构造F检验统计量

设分类自变量有K个处理，可以将每个处理看成一个子总体，则有总体：

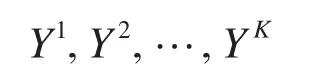
从这K个子总体抽取如下样本：

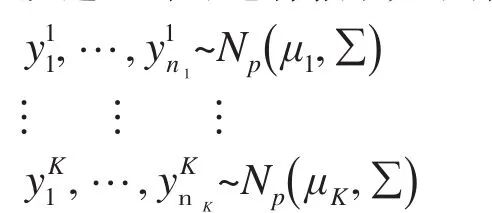
其中是 相 互 独 立的。按照上文的内容，选择一个p维向量l′与所有样品相乘，得出线性组合后的样本：

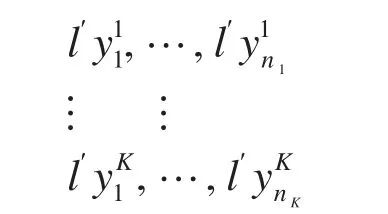
样本数据经过线性组合后均变成了一维数据，由上文可知，检验H0:至少有一组i≠j，使得μi≠μj与检验H0:至少有一组i≠j，使得≠是等价的。这样就将多元方差分析转换为一元方差分析。可以构造F检验统计量进行一元方差分析。这里存在两个问题：第一个问题是该样本数据经历线性组合之后是否仍然服从正态分布；第二个问题是变换后的样本数据的组间离差平方和与组内离差平方和是否仍然独立。接下来分别论证这两个问题。

2.1 样本数据线性组合后正态性证明

在一元正态分布中，若Z~N(0 ，1) ，则X=μ+σ Z~N(μ，σ2)。类似的在多元正态分布中，可以类似的定义多元正态分布。设相互独立且有相同的分布N(0 ，1)，μ为p维常数向量，A为p阶常数矩阵，则称：x=μ+的分布为多元正态分布，记作

可以利用上述定义证明样本数据进行线性组合后仍然服从正态分布。具体过程如下：

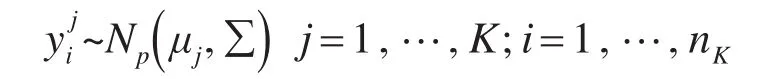
协差阵∑可以分解为：∑=

则可以写成μj+

则

故得证。

2.2 线性组合后的数据组间离差与组内离差平方和独立性证明

由上知样本数据进行线性组合后仍然服从正态分布，可以计算出变换后的样本数据的总离差平方和SST、组间离差平方SSB和组内离差平方和SSE，经过适当变形之后总离差平方和SST、组间离差平方SSB和组内离差平方和SSE均服从卡方分布，若组间离差平方SSB和组内离差平方和SSE相互独立，则可以构造出F检验统计量进行方差分析。下面证明组间离差平方SSB和组内离差平方和SSE相互独立。

变换后样本数据的总离差平方和SST、组间离差平方SSB和组内离差平方和SSE为：

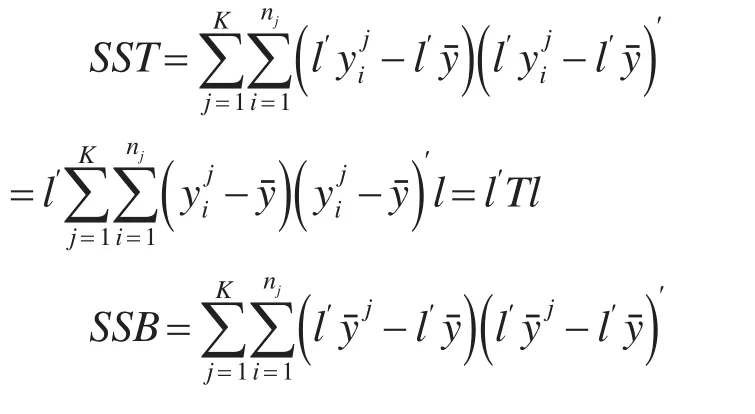
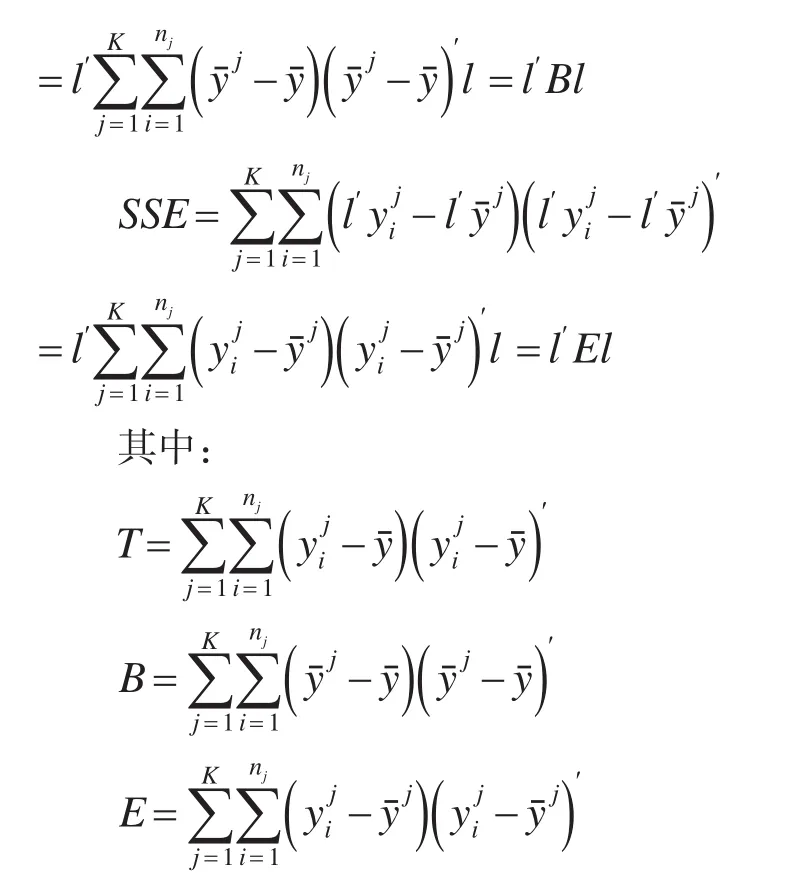
p维行向量l′为一个常数向量，要证明组间离差平方SSB和组内离差平方和SSE之间相互独立，即证明组间离差阵B和组内离差阵E相互独立。随机矩阵的独立性可以利用的科克朗（Cochran）定理来证明：设X~Nn×p(M，In⊗Σ )，C和D为n阶对称矩阵，X′CX与X′DX独立，当且仅当CD=0。另外，若A是投影阵则I-A也是投影阵并且有A(I-A)=0成立。利用科克朗（Cochran）定理以及投影阵的性质，可以很方便地证明组间离差平方SSB和组内离差平方和SSE之间相互独立。具体证明过程如下：

资料阵Y~Nn×p(M，In⊗Σ )，其中M的各行是各个子总体的均值向量的转置按照各个子总体的观测次数重复排列而成。

可以将总离差阵改写成：

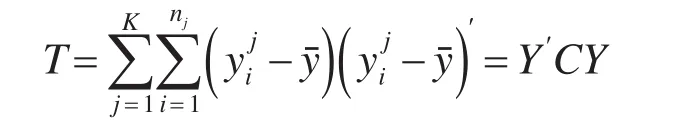
其中：

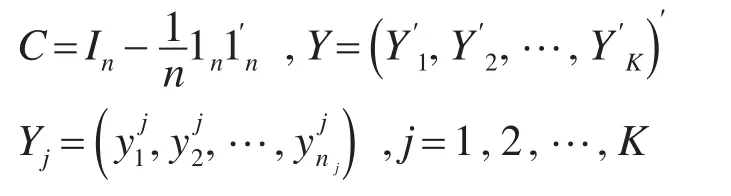
可以验证：

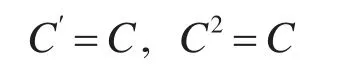
故C为投影阵且rank(C)=n-1；

类似的有：

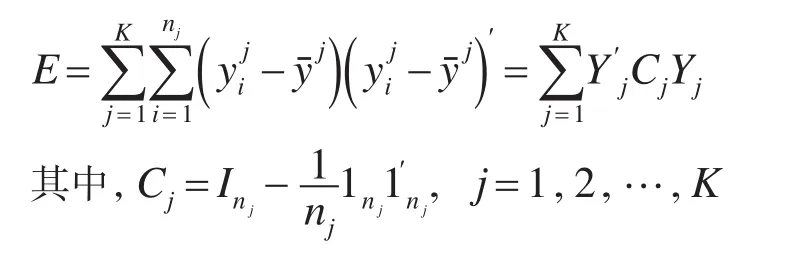
也可以将组内离差阵E写成：E=Y′C*Y

其中，C*=diag(C2，…，CK)

显然C*也是投影阵并且rank(C*)=rank(C1)+rank(C2)+…+rank(CK)=n-K；

组间离差阵B可以改写成：

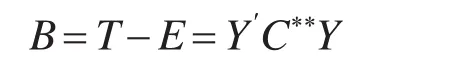
其中，

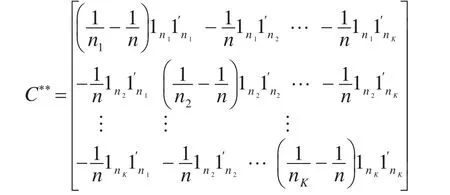
显然有，C**=C**′， (C**)2=C**，故C**是投影阵并且rank(C**)=trC**=trC+trC*=K-1。

C，C*，C**均为投影阵，并且有C=C*+C**，所以C*C**=0，由科克朗（Cochran）定理知组间离差阵B和组内离差阵E是相互独立的，故组间离差平方SSB和组内离差平方和SSE之间相互独立。

综上所述，本文可以构造出F检验统计量：

3 构建检验法则

可以将原假设和备择假设设为：

H0:H0:存在μi≠μj，i≠j；H1:μ1=…=μK

由上文知，可以将原假设和备择假设改写成：

H0:存在l′μi≠l′μj，i≠j；H1:l′μ1= … =l′μK

并且这两组原假设和备择假设的检验结果是等价的。检验统计量为:

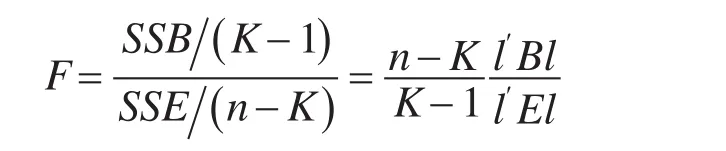
是一个已知分布的统计量，只需要给出显著性水平α就可以确定拒绝域的临界值Fα即得出检验法则。

该F检验统计量与一般的F统计量有所不同，其中的p维行向量l′事先并不知道，所以无法计算出检验统计量的具体数值。但考虑到检验的初衷：拒绝与本文观点对立的观点，从而证明本文的观点是正确的。故只需要找到一个特例说明与本文观点对立的观点是错误的。原假设H0:存在l′μi≠l′μj，i≠j成立时，即系统误差不为零。所以组间离差平方和与组内离差平方和应该相差很大。若将样本观测值带入检验统计量F，计算得出的结果很小，小到可以看成是一个小概率事件，则我们有充分的理由拒绝原假设。所以上述的假设检验问题就转化为已知样本数据的条件下求解F检验统计量的最小值，再与临界值Fα（下分为数）做出比较。F检验统计量的最小值的计算过程如下：

组内离差阵组间离差阵显然E、B为正定矩阵并且是对称矩阵，检验统计量F可以改写成：

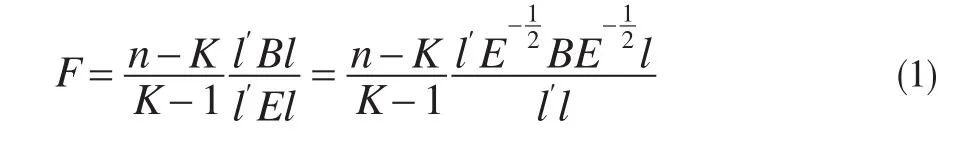
其中是p阶对称矩阵，故其特征值是实数；又因为为正定矩阵，故其特征值全部大于零。

由矩阵的谱分解知：

其中λ1≥λ2≥…≥λp为B相对于E的广义特征值，β1，β2，…，βp为B相对于E的广义特征值λ1≥λ2≥…≥λp所对应的标准化特征向量。β2，…，βp为一组线性无关的p维向量，对β2，…，βp做适当变换后，可以将其看成p维向量空间中的一组标准正交基，该正交基仍然记作β2，…，βp。

由向量的线性表出知：

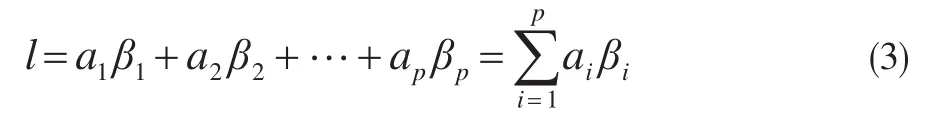
其中a2，…，ap为常数。

将式（2）、式（3）带入式（1）得：

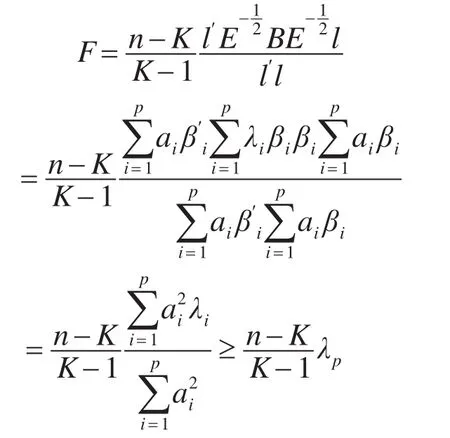
当l=βp时，等号成立。

综上所述，检验法则为：当时，有充分理由拒绝原假设，接受备择假设；当时，不拒绝原假设。

4 利用投影思想进行多元方差分析的优点

传统的构造检验统计量的步骤为：先构造出一个统计量，该统计量的分布是不为我们所熟悉的，为此一般的做法是将该统计量做适当变换使得变换后的统计量的分布渐近服从一个我们熟悉的分布即F分布。这一过程通常计算量较大，并且理论性强不易理解。若直接从投影后的样本资料出发构建F分布。首先，从推导过程中可以发现，所使用的都是基本的统计知识以及一些线性代数知识，推导过程也十分简单，可以方便大家理解以及运用该分析方法；其次，随着计算机的普及以及储存技术的发展，所研究的数据往往是海量、高维的数据，这是挖掘数据中有价值信息的一个障碍，利用投影思想可以将高维度数据变换成低维度，这种思想的应用无疑带来了巨大的便利。

5 模拟

为了证实方法的正确性，分两步进行模拟。

第一步利用R软件产生9个子总体，每个子总体有20个样品，这9个子总体的均值向量和协方差阵相同，所有样品均为5维向量（见表2），其中均值向量和协方差阵是随机选取的，在此基础上进行多元方差分析，验证检验结果是否能够拒绝原假设。

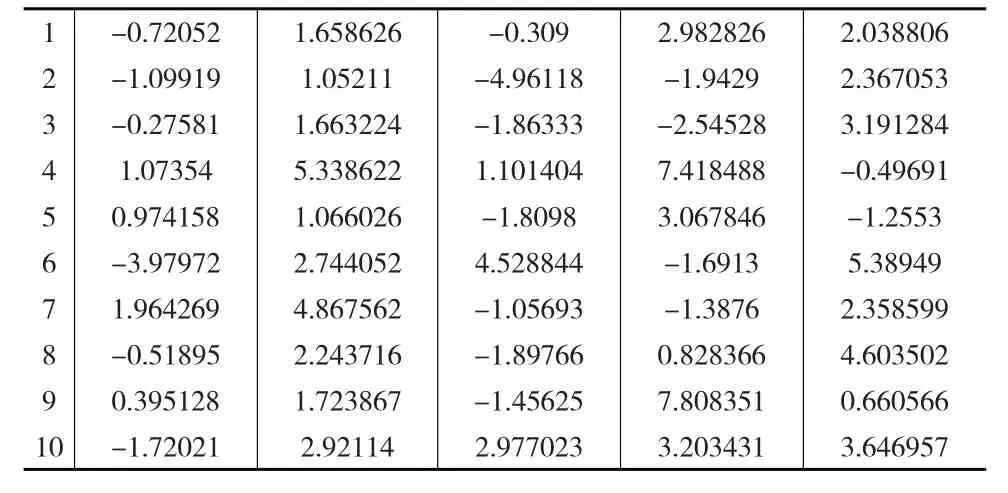
表2 第一个子总体前十个样品的5维向量

利用计算出的组间离差阵相对于组内离差阵最小广义特征值为λp=0.0129，故F检验统计量的取值为F=，该分位点对应的p=0.02703，非常接近0，因此有充分理由拒绝原假设。

第二步继续利用R软件产生9个子总体，每个子总体有20个样品，与第一步不同的是，这9个子总体的均值向量不相同，所有样品均为5维向量（见表3），其中均值向量和协差阵是随机选取的，在此基础上进行多元方差分析，验证检验结果是否为不能拒绝原假设。

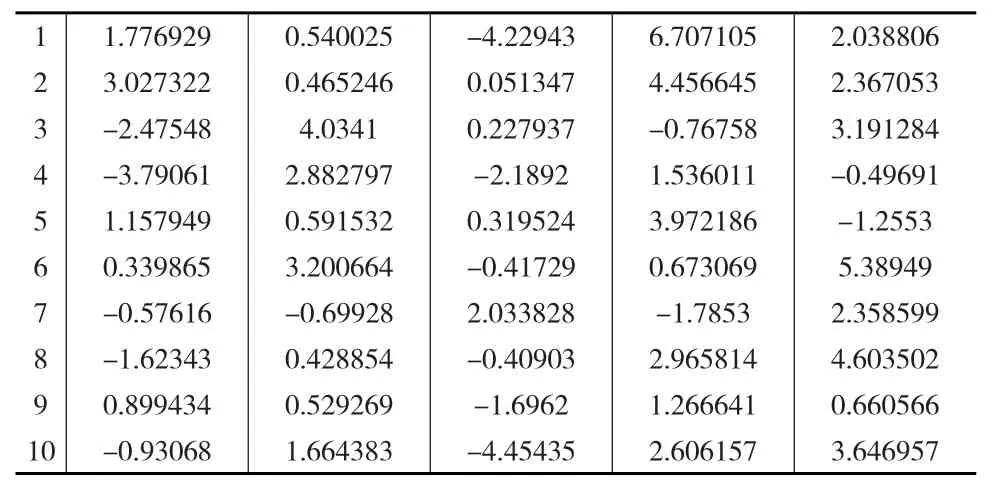
表3 第一个子总体前十个样品的5维向量

利用计算出的组间离差阵相对于组内离差阵最小广义特征值为λp=0.0228，故F检验统计量的取值为F=，该分位点对应的p=0.136，不是一个非常小的数值，因此没有充分理由拒绝原假设。

6 结论

本文首先利用投影思想构建的F检验统计量在模拟试验中，当各个子总体均值向量之间不存在差异时，检验结果拒绝原假设，接受备择假设；当各个子总体均值向量之间确实存在差异，F检验统计量的取值不能够拒绝原假设，故可以达到多元方差分析的目的。在假设检验过程中，当没有充分理由拒绝原假设时，这时很多人便认为原假设是正确的。赞同这个观点的人并没有考虑原假设错误但检验统计量取值没有落入拒绝域中的概率的大小（即纳伪的概率），若原假设错误时建议统计量取值没有落入拒绝域中的概率很大，这时认为原假设是正确的显然是不可信的。此时可以认为检验工作并没有取得实质进展。如何有效克服这个问题有待更进一步的探讨。

参考文献：

[1] Finch H.Comparison of the Performance of Nonparametric and Para⁃metric MANOVA Test Statistics When Assumptions Are Violated[J].Methodology,2005,1(1).

[2] Kapstad H,Hanestad B R,Langeland N,et al.Cutpoints for Mild,Moderate and Severe Pain in Patients With Osteoarthritis of the Hip or Knee Ready for Joint Replacement Surgery[J].BMC Musculoskele⁃tal Disorders,2008,9(1).

[3] Hatlen M A,Arora K,Vacic V,et al.Integrative Genetic Analysis of Mouse and Human AML Identifies Cooperating Disease Alleles[J].The Journal of Experimental Medicine,2016,213(1).

[4] Ullah I,Jones B.Regularised Manova for High-Dimensional Data[J].Australian&New Zealand Journal of Statistics,2015,57(3).

[5] Chiani M.Distribution of the Largest Root of a Matrix for Roy’s Test in Multivariate Analysis of Variance[J].Journal of Multivariate Analy⁃sis,2016,(143).

[6] Haase R F,Ellis M V.Multivariate Analysis of Variance[J].Journal of Counseling Psychology,1987,34(4).

[7] Stevens J P.Power of the Multivariate Analysis of Variance Tests[J].Psychological Bulletin,1980,88(3).

[8] Olson C L.On Choosing a Test Statistic in Multivariate Analysis of Variance[J].Psychological Bulletin,1976,83(4).